SECTION 6 3 Compound Interest and Continuous Growth

SECTION 6. 3 Compound Interest and Continuous Growth Copyright © Cengage Learning. All rights reserved.

Learning Objectives 1 Use the compound interest formula to calculate the future value of an investment 2 Construct and use continuous growth models 3 Use exponential models to predict and interpret unknown results 2

Compound Interest 3

Compound Interest 4

Example 1 – Compound Interest Consider the following situation. In April 2007, Heritage Bank offered a 1 -year certificate of deposit (CD) with a minimum investment of $1000 at a nominal interest rate of 4. 42% compounded quarterly. (Nominal means “in name only. ”) What is the value of the CD after 1 year? 5

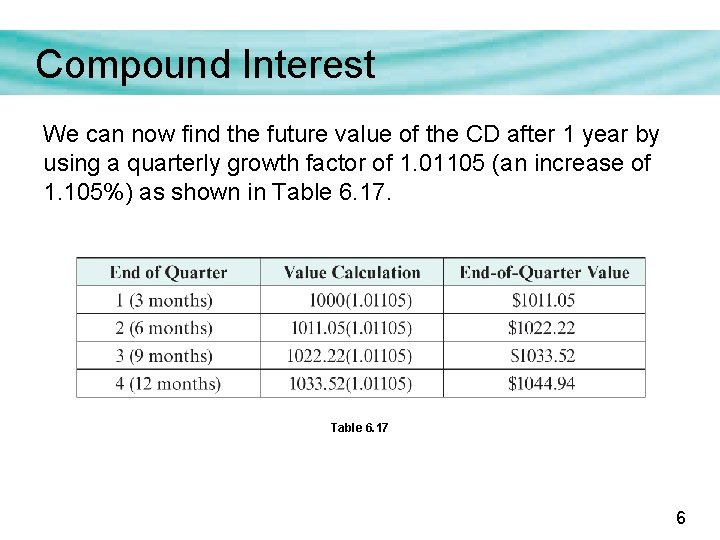
Compound Interest We can now find the future value of the CD after 1 year by using a quarterly growth factor of 1. 01105 (an increase of 1. 105%) as shown in Table 6. 17 6

Compound Interest Note that the interest payments continue to increase throughout the year. This is due to compound interest, which occurs when interest is paid on the initial amount invested as well as all previously earned interest. 7

The Compound Interest Formula Table 6. 19 shows compounding frequencies and associated formulas for compound interest. Table 6. 19 8

Example 2 – Comparing Future Values In March 2007, Met. Life Bank advertised a 5 -year CD with a 4. 64% nominal interest rate compounded daily. Assuming someone could continue to invest their money at this rate and compounding frequency up until retirement at age 65, compare the future value of a $5000 investment of a 25 -year-old to the future value of a $10, 000 investment for a 45 -year-old. Assume no additional deposits or withdrawals are made. 9

Example 1 – Solution The 25 -year-old will be accumulating interest 365 days a year for 40 years (the time until she retires), while the 45 -year-old will be accumulating interest 365 days a year for 20 years (the time until he retires). Using the compound interest formula, we have 10

Example 1 – Solution cont’d Deducting the amount of the initial investment, we see that the 25 -year-old earned $26, 986. 69 in interest while the 45 -year-old earned $15, 292. 96 in interest. 11

The Compound Interest Formula Compound Interest as an Exponential Function Since compound interest causes an account to grow by a fixed percent each year, we may categorize the compound interest formula as an exponential function. First, consider the following property of exponents. 12

The Compound Interest Formula From this property we can rewrite the compound interest formula as follows. If we then let can rewrite the compound interest formula in the form y = abx. A = Pbt 13

The Compound Interest Formula The annual percentage yield (APY) is the actual amount of interest earned during the year and takes into account not only the nominal rate but also the compounding frequency. The Truth in Savings Act of 1991 requires banks to publish the APY for all savings accounts and CDs so consumers can more easily compare offers from different banks and make informed financial decisions. 14

The Compound Interest Formula 15

Example 3 – Modeling Compound Interest with Exponential Functions An investor makes a $3000 initial deposit in a CD with a 3. 68% interest rate compounded weekly. a. Use the compound interest formula to find an exponential function to model the future value of the investment. b. Determine the annual percentage yield for the investment. 16

Example 3(a) – Solution So models the future value of the CD. 17

Example 3(b) – Solution cont’d From the exponential model, we can see the annual growth factor is 1. 0375 and the corresponding annual percentage yield is 3. 75% (1. 0375 – 1). 18

Continuous Growth Factor 19

Example 4 – Finding the Continuous Growth Factor Using the compound interest formula, examine what happens to $1 invested in an account with a 100% interest rate if interest is compounded an increasing number of times per year. Discuss what you discover. Solution: Based on the examples we have seen thus far, it appears that the value of the account will increase as we increase the compounding frequency. 20

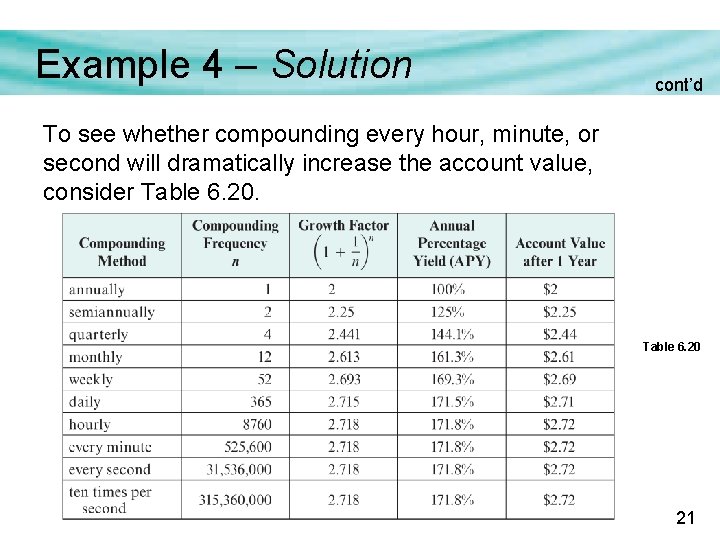
Example 4 – Solution cont’d To see whether compounding every hour, minute, or second will dramatically increase the account value, consider Table 6. 20 21

Example 4 – Solution cont’d The table reveals an interesting result. It appears the account will never be worth more than $2. 72 after 1 year, and the maximum annual growth (APY) will never be more than 171. 8% (a growth factor of approximately 2. 718). This number ( 2. 718) is so important in mathematics that it has its own name: e. 22

The Compound Interest Formula We represent the notion of infinitely large n by using the term continuous compounding. 23

Example 5 – Continuous Compound Interest Find the future value after 4 years of $2000 invested in an account with a 5. 3% nominal interest rate compounded continuously. Solution: Using the formula for continuous compound interest, we have 24

Example 5 – Solution cont’d After 4 years, the account will be worth $2472. 30. 25

e: The Natural Number 26

Converting from General Form to Using e Consider the following situation. The total annual healthrelated costs in the United States in billions of dollars can be modeled by the function where t is the number of years since 1960. 27

e: The Natural Number The function H is similar to continuous compound interest, so we could use an exponential function involving the number e to model the annual health-related expenditures. Since we are not dealing with an interest-bearing account, we will use the more generalized form of f (x) = aekx instead of the more specific A = Pert. By finding the value of k such that ek = b, we can rewrite the exponential function using the number e. 28

e: The Natural Number We see that k = 0. 09649, so e 0. 09649 = 1. 1013. Thus, we rewrite H as The functions and are equivalent, provided we disregard round-off error. 29

Example 6 – Converting f (x) = aekx to f (x) = abx Rewrite the function f (x) = 1000 e 0. 07 x in the form f (x) = abx. Solution: Since b = ek, we can find the growth factor b by evaluating e 0. 07. 30

Continuous Growth (Decay) Rate 31

Continuous Growth (Decay) Rate We know that functions of the form f (x) = abx exhibit exponential growth when b > 1 and exponential decay when b < 1. Since b = ek, what effect does k have on the value of b? Let’s consider the results when k = 0. 1 and when k = – 0. 1. It appears that f (x) = aekx has exponential growth when > 0 and exponential decay when k < 0. k 32

Continuous Growth (Decay) Rate 33