CHAPTER 7 International Arbitrage And Interest Rate Parity

CHAPTER 7 International Arbitrage And Interest Rate Parity

Chapter Overview A. International Arbitrage B. Interest Rate Parity (IRP)

Chapter 7 Objectives This chapter will: A. Explain the conditions that will result in various forms of international arbitrage, along with realignments that will occur in response to various forms of international arbitrage B. Explain the concept of interest rate parity and how it prevents arbitrage opportunities
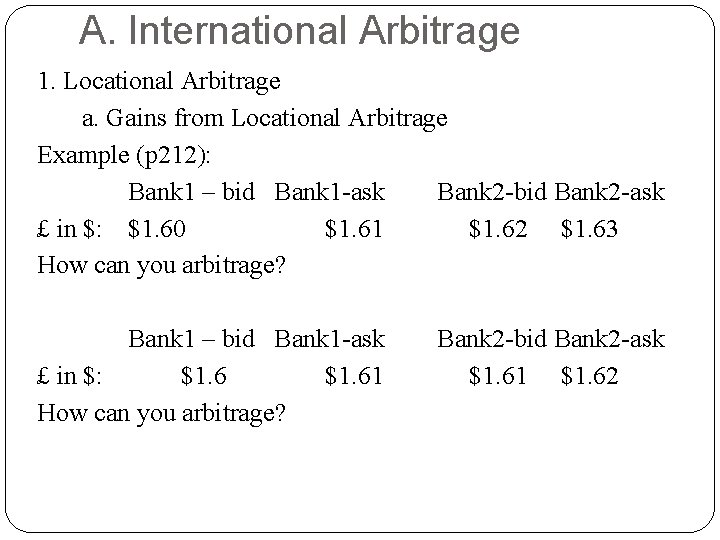
A. International Arbitrage 1. Locational Arbitrage a. Gains from Locational Arbitrage Example (p 212): Bank 1 – bid Bank 1 -ask Bank 2 -bid Bank 2 -ask £ in $: $1. 60 $1. 61 $1. 62 $1. 63 How can you arbitrage? Bank 1 – bid Bank 1 -ask Bank 2 -bid Bank 2 -ask £ in $: $1. 61 $1. 62 How can you arbitrage?

A. International Arbitrage Example : If you start with $10, 000 and conduct one round trip transaction, how many $ will you end up with ? b. Realignment due to Locational Arbitrage: arbitrage opportunity will disappear eventually.

A. International Arbitrage 2. Triangular Arbitrage a. Cross exchange rate: In US, it represents relationship between two non dollar currencies. Example: £= $1. 6; C$ = $0. 8, so value of £ in units of C$ = $1. 6 / $0. 8 =2. so value of C$ in units of £= $0. 8/ $1. 6 =0. 5. b. £ is quoted at $1. 60. Malaysian Rinnggit (MYR) is quoted at $0. 20 and the cross exchange rate is £ 1 = MYR 8. 1 How can you arbitrage?
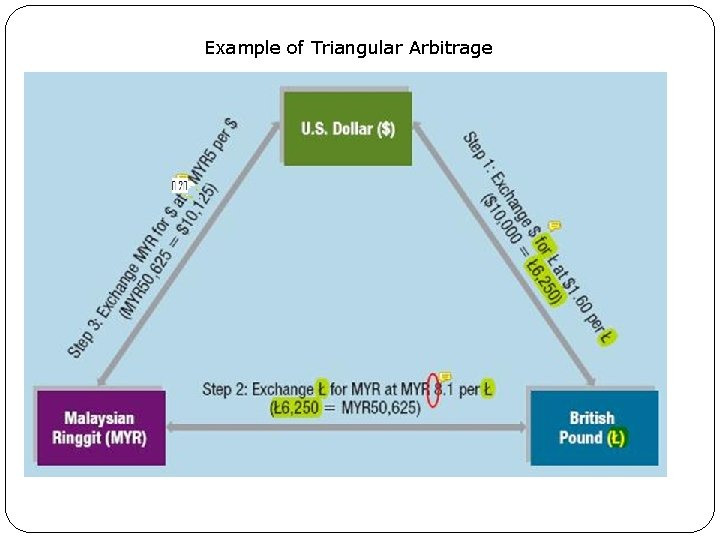
Example of Triangular Arbitrage Exhibit 7. 3

A. International Arbitrage 2. Triangular Arbitrage C. Accounting for the Bid/Ask Spread Example : How can you arbitrage? Rearrange: Bid of Pound / Rinngit = 1. 6/0. 2=8 MYR/£ Ask of Pound/Rinngit = 1. 61/0. 201=8. 01 MYR/£ There does exist arbitrage opportunity. With Rinngit in hand, you can buy pound at ask (sell Rinngit) @ 8. 01 MYR/£. Then you can sell pound at bid @8. 1 MYR/£ and make profits, if this quote is available. If not, how can you arbitrage?
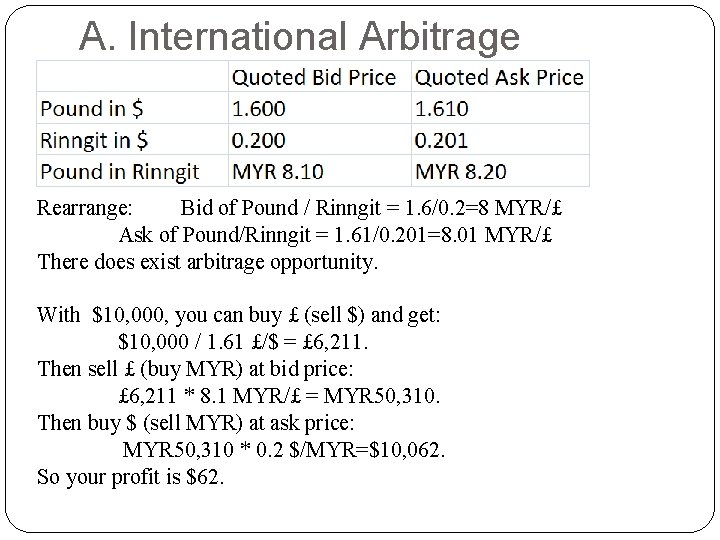
A. International Arbitrage Rearrange: Bid of Pound / Rinngit = 1. 6/0. 2=8 MYR/£ Ask of Pound/Rinngit = 1. 61/0. 201=8. 01 MYR/£ There does exist arbitrage opportunity. With $10, 000, you can buy £ (sell $) and get: $10, 000 / 1. 61 £/$ = £ 6, 211. Then sell £ (buy MYR) at bid price: £ 6, 211 * 8. 1 MYR/£ = MYR 50, 310. Then buy $ (sell MYR) at ask price: MYR 50, 310 * 0. 2 $/MYR=$10, 062. So your profit is $62.

A. International Arbitrage 2. Triangular Arbitrage c. Realignment due to Triangular Arbitrage Triangular arbitrage would force the exchange rates back into equilibrium

A. International Arbitrage 3. Covered Interest Arbitrage (CIA): It is a process of capitalizing on the interest rate differential between two countries while covering exchange rate risk with a forward contract. Steps, assuming foreign interest rate is higher: a. Borrow from local bank @ local rate. b. Convert to foreign currency and invest in foreign bank, for higher interest rate. c. Meanwhile, sell a forward contract with the same maturity as in b, to eliminate potential exchange rate risk. d. At maturity, convert back to $ at pre-determined forward rate.
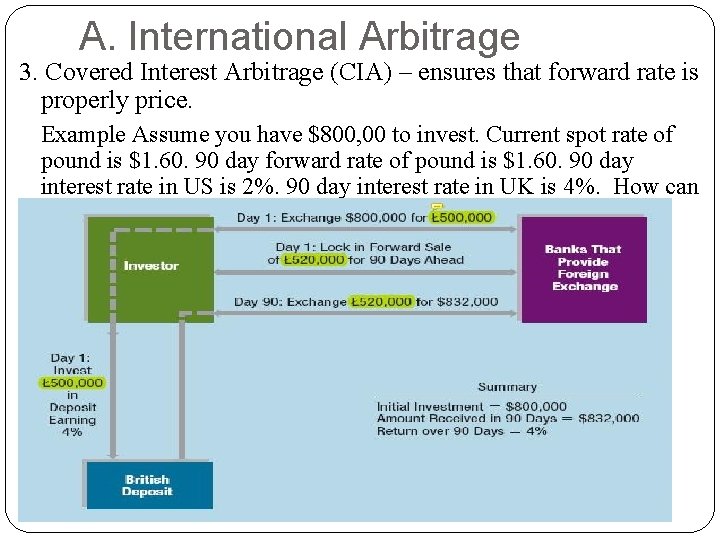
A. International Arbitrage 3. Covered Interest Arbitrage (CIA) – ensures that forward rate is properly price. Example Assume you have $800, 00 to invest. Current spot rate of pound is $1. 60. 90 day forward rate of pound is $1. 60. 90 day interest rate in US is 2%. 90 day interest rate in UK is 4%. How can you arbitrage?
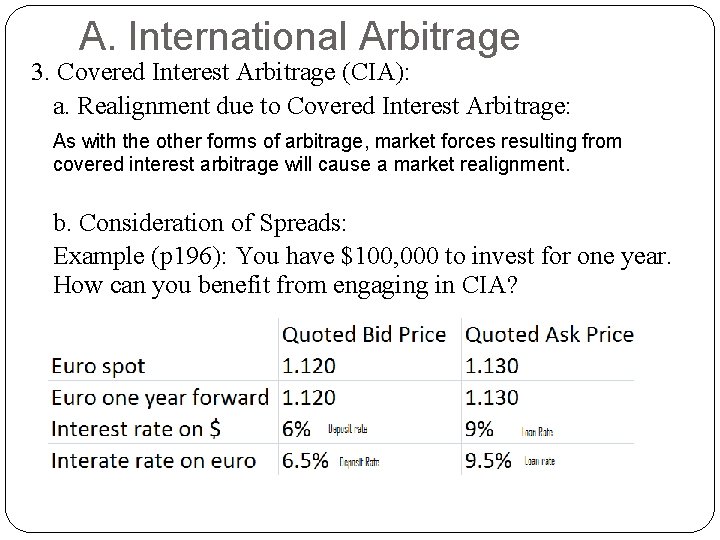
A. International Arbitrage 3. Covered Interest Arbitrage (CIA): a. Realignment due to Covered Interest Arbitrage: As with the other forms of arbitrage, market forces resulting from covered interest arbitrage will cause a market realignment. b. Consideration of Spreads: Example (p 196): You have $100, 000 to invest for one year. How can you benefit from engaging in CIA?

A. International Arbitrage 3. Covered Interest Arbitrage (CIA): c. Comparison of arbitrage effects: Locational arbitrage: quoted exchange rates among banks are similar. Triangular arbitrage: cross exchange rates are properly set. CIA: forward exchange rates are properly set.

B. Interest Rate Parity (IRP) Interest rate parity: Forward rate differs from the spot rate by a sufficient amount to offset the interest rate differences between two currencies. If IRP does not hold, CIA is possible. 2. Determining the Forward Premium: a. Relationship between Forward Premium and Interest Rate Differential: p = (F-S)/S = ih-if. p: forward rate premium or discount F: Forward rate, quoted as home currency/ foreign currency 1. (meaning: foreign currency in home currency or how many home currency per foreign currency) S: Spot rate, quoted as home currency/ foreign currency (meaning: foreign currency in home currency or how many home currency per foreign currency) ih: interest rate of home currency. if: interest rate of foreign currency.

Interest Rate Parity 1 + i$ F$/¥ = 1 + i¥ S$/¥ i$ – i¥ ≈ F – S S 6 -16

Interest Rate Parity 1 + i¥ F¥/$ = 1 + i$ S¥/$ 6 -17 or 1 + i$ F$/¥ = 1 + i¥ S$/¥

Interest Rate Parity Carefully Defined 1 + i¥ F¥/$ = S¥/$ × 1 + i$ 6 -18 or 1 + i$ F$/¥ = S$/¥ × 1 + i ¥

Interest Rates and Exchange Rates The Forward Rate A forward rate is an exchange rate quoted today for settlement at some future date The forward exchange agreement between currencies states the rate of exchange at which a foreign currency will be bought or sold forward at a specific date in the future (typically 30, 60, 90, 180, 270 or 360 days) The forward rate is calculated by adjusting the current spot rate by the ratio of euro currency interest rates of the same maturity for the two subject currencies 7 -19

B. Interest Rate Parity (IRP) 2. Determining the Forward Premium: a. Example: ih is 5%; if is 6%; then p = 0. 05 - 0. 06= 0. 01. Meaning: Forward rate is 1% lower than the spot rate. Example: If the foreign currency’s spot rate is $0. 10. Then what is the foreign currency’s forward rate? F= S(1+p) = $0. 10 *(1 -0. 01) = $0. 099. Note: Page 199’s example use p = (1+ ih)/(1+if)-1. The right side approximates to ih-if. So p= ih-if.

Interest Rate Parity (IRP) In the diagram in the following slide, a US dollar- based investor with $1 million to invest, is shown indifferent between dollar-denominated securities for 90 days earning 8. 00% per annum, or Swiss franc-denominated securities of similar risk and maturity earning 4. 00% per annum, when “cover” against currency risk is obtained with a forward contract 7 -21
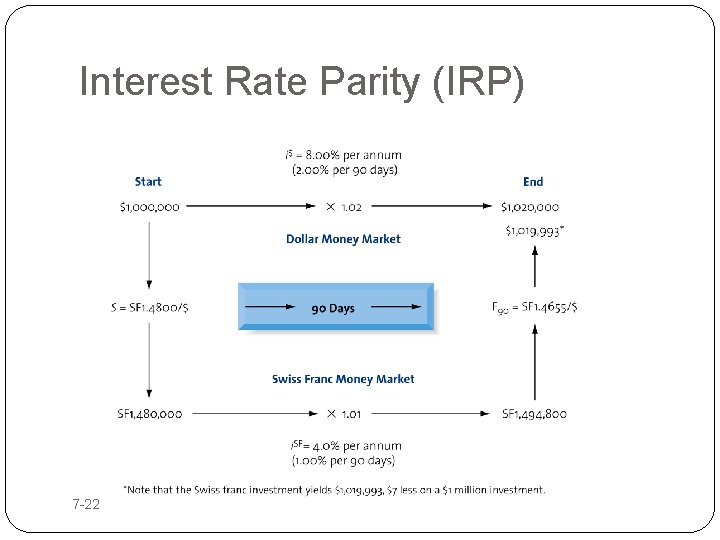
Interest Rate Parity (IRP) 7 -22

Covered Interest Arbitrage (CIA) Because the spot and forward markets are not always in a state of equilibrium as described by IRP, the opportunity for arbitrage exists The arbitrageur who recognizes this imbalance can invest in the currency that offers the higher return on a covered basis This is known as covered interest arbitrage (CIA) The following slide describes a CIA transaction in much the same way as IRP was transacted 7 -23

Exhibit 6. 7 Covered Interest Arbitrage (CIA) 7 -24

B. Interest Rate Parity (IRP) 3. Graphic Analysis of Interest Rate Parity a. Points Representing a Discount: F <S, when ih < if b. Points Representing a Premium: F >S, when ih > if c. Points representing IRP: When IRP holds & CIA is not feasible. d. Points below the IRP Line (Such as points of X and Y in previous slide): CIA exist but how and investors can make positive profits from CIA? Explain (see next slide). e. Points above the IRP Line (Such as point Z in previous slide): CIA exist but how and investors can make positive profits from CIA? Explain (see next slide).
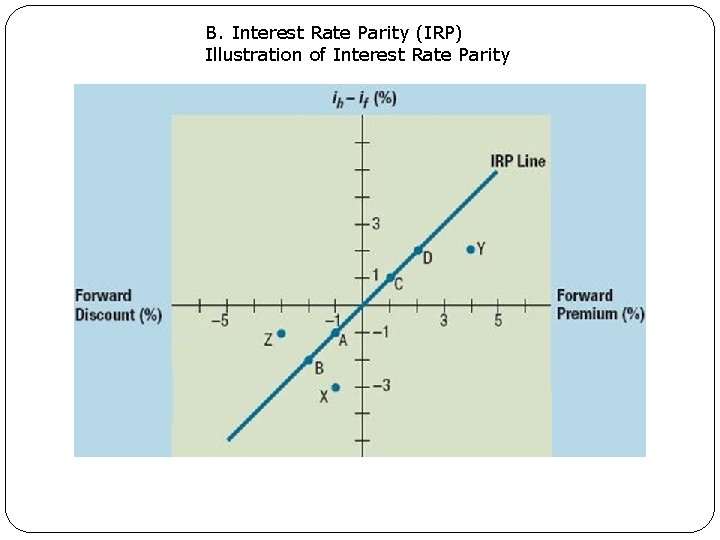
B. Interest Rate Parity (IRP) Illustration of Interest Rate Parity 7. 9

B. Interest Rate Parity (IRP) 3. Graphic Analysis of Interest Rate Parity d. Answer: @ Y, forward premium >ih-if forward rate is set too high and more than offset the interest differential So you should change $ to foreign currency @ if and sell forward contract At maturity, convert foreign currency back to $ at forward rate return equals to: CIA =Principal / S *(1+if * 90/360) * F Invest in home country = principal *(1+ih * 90/360) Extra profits to engage in CIA beyond holding home currency = Principal / S *(1+if * 90/360) * F - principal *(1+ih * 90/360) ---- assume 90 day to mature. Same strategy for @X when forward rate is set too high. Example: ih is 4% and if is 2%. S is $1. 5/£ and F is $2/£. Extra Profits to engage in CIA= 1 / 1. 5 * (1+0. 02/360*90) *2 – 1*(1+0. 04/360*90) =1. 34 – 1. 01 = $0. 23. So he can make $0. 23 as extra profits for CIA beyond holding home currency.

B. Interest Rate Parity (IRP) 3. Graphic Analysis of Interest Rate Parity e. Answer: @ Z, forward premium >ih-if forward rate is set too low and less than enough to offset the interest differential CIA is not feasible to US investors hold $ @ local bank. Invest in home country = principal *(1+ih * 90/360) To foreign investors, they can adopt CIA, since rate of two currencies are “inverse” of each other and CIA exists not for US investors, but foreign investors. Example: ih is 2% and if is 4%. S is $1. 5/£ and F is $1. 1/£. To UK investor, they can convert £ to $, sell forward contract $ for £. Return from CIA = £ 1 * $1. 5/£ *(1+ 0. 02 * 90/360)/ ($1. 1/£) = £ 1. 37. This is greater than investing in local bank to £ holder, whose return is: £ 1*(1+0. 04*90/360)=£ 1. 01. So UK investor can make £ 0. 36 as extra profits for CIA beyond holding home currency.

Covered Interest Arbitrage (CIA) A deviation from CIA is uncovered interest arbitrage, UIA, wherein investors borrow in currencies exhibiting relatively low interest rates and convert the proceeds into currencies which offer higher interest rates The transaction is “uncovered” because the investor does not sell the currency forward, thus remaining uncovered to any risk of the currency deviating 7 -29

B. Interest Rate Parity (IRP) and CIA Rule of Thumb: All that is required to make a covered interest arbitrage profit is for interest rate parity not to hold. The key to determining weather to start CIA is to compare the differences in interest rate to the forward premium. Arbitrage rule of thumb: If the difference in interest rates is greater than the forward premium, invest in the higher interest yielding currency. If the difference in interest rates is less than the forward premium, invest in the lower interest yielding currency.

B. Interest Rate Parity (IRP) 4. How to Test Whether Interest Rate Parity Exists 5. Interpretation of Interest Rate Parity: If IRP exists, investors cannot use covered interest arbitrage to achieve higher return than those achievable in their home countries. Example: ih(US) is 5% and if (UK) is 7%, then if IRP exists US investors can make 5% either in local bank (US) or with CIA; UK investors can make 7% either in local bank (UK) or with CIA. 6. Does Interest Rate Parity Hold? Empirical studies generally support IRP.

B. Interest Rate Parity (IRP) 7. Consideration When Assessing Interest Rate Parity a. Transaction Costs: Typical transaction costs in recent years have been in the range of 0. 18% to 0. 25% on an annual basis.

B. Interest Rate Parity (IRP) 7. Consideration When Assessing Interest Rate Parity b. Political Risk (Capital Controls) Forward contract lock in the forward rate, but what about foreign government does not allow this reconversion? Default risk exist foreign investments, including foreign treasury bills. c. Differential Tax Laws might make CIA not worth trying. Story: Japanese housewives play the Yen Carry Trade.

B. Interest Rate Parity (IRP) 8. Forward rate as an unbiased predictor of the future spot rate: Some forecasters believe that foreign exchange markets for the major floating currencies are efficient and forward exchange rates are unbiased predictors of the future spot rate. It is unbiased predictor, does not mean that the future spot rate will actually be equal to what the forward rate predicts. Unbiased prediction simply means that the forward rate will, on average, overestimate and underestimate the actual future spot rate in equal frequency and degree. The forward rate may, in fact, never actually equal the

Exhibit 6. 10 Forward Rate as an Unbiased Predictor for Future Spot Rate 7 -35
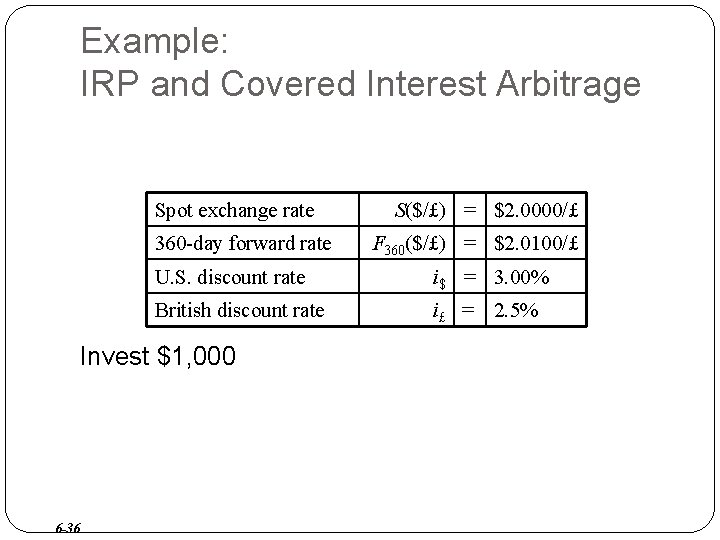
Example: IRP and Covered Interest Arbitrage Spot exchange rate 360 -day forward rate F 360($/£) = $2. 0100/£ U. S. discount rate i$ = 3. 00% British discount rate i£ = 2. 5% Invest $1, 000 6 -36 S($/£) = $2. 0000/£

Interest Rate Parity & Exchange Rate Determination According to IRP only one 360 -day forward rate, F 360($/£), can exist. It must be the case that F 360($/£) = $2. 01/£ Why? 6 -37

If invest in local bank at 2. 5%, $1, 000 you get: $1000*(1+0. 03) = $1, 030 CIA process: CIA step 1: Convert to £ at current spot rate, you get: $1000 / 2. 0 $/£=500 £ £ 500 6 -38 1. Convert to£ and sell forward contract to lock in the rate to exchange back to $. 2. Save £ into UK bank. 3. Sell £ for $ at forward rate. This example is that IRP does not hold and therefore, there is no arbitrage opportunities. CIA step 2: Save in UK bank at 3%, you get: £ 500 *(1+0. 025)= £ 512. 5 CIA step 3: Sell £ @ forward rate, you get: £ 512. 5 *2. 01$/£ =$1030. £ 512. 5

Arbitrage Strategy I If F 360($/£) > $2. 01/£ , e. g. F 360($/£) = $2. 50/£ 6 -39

If invest in local bank at 2. 5%, $1, 000 you get: $1000*(1+0. 03) = $1, 030 < $1, 281 CIA process: CIA step 1: Convert to £ at current spot rate, you get: $1000 / 2. 0 $/£=500 £ £ 500 6 -40 1. Convert to£ and sell forward contract to lock in the rate to exchange back to $. 2. Save £ into UK bank. 3. Sell £ for $ at forward rate. This example is that IRP does not hold and therefore, there is arbitrage opportunities by taking CIA step 2: Save in UK bank at 3%, you get: £ 500 *(1+0. 025)= £ 512. 5 CIA step 3: Sell £ @ forward rate, you get: £ 512. 5 *2. 5$/£ =$1281. 25 £ 512. 5

Arbitrage Strategy II If F 360($/£) < $2. 01/£, e. g. F 360($/£) = $1. 90/£ 6 -41

If invest in local bank at 2. 5%, $1, 000 you get: $1000*(1+0. 03) = $1, 030 > $974 CIA process: CIA step 1: Convert to £ at current spot rate, you get: $1000 / 2. 0 $/£=500 £ £ 500 6 -42 1. Convert to£ and sell forward contract to lock in the rate to exchange back to $. 2. Save £ into UK bank. 3. Sell £ for $ at forward rate. This example is that IRP does not hold. But, there is no arbitrage opportunities by taking CIA in US. CIA step 2: Save in UK bank at 3%, you get: £ 500 *(1+0. 025)= £ 512. 5 CIA step 3: Sell £ @ forward rate, you get: £ 512. 5 *1. 90$/£ =$973. 75 £ 512. 5

Transactions Costs Example (FYI) Will an arbitrageur facing the following prices be able to make money? Borrowing Lending $ 5. 0% 4. 50% € 5. 5% 5. 0% Bid Ask Spot $1. 42 = € 1. 00 $1. 45 = € 1, 00 F($/ €) = S($/ €) × (1 + i$) (1 + i€) Forward $1. 415 = € 1. 00 $1. 445 = € 1. 00 b F 1($/€) = 6 -43 a b S (1+i ($/€) $) 0 (1+i€l ) a F 1($/€) = b l S (1+i ($/€) $) 0 (1+i€b)
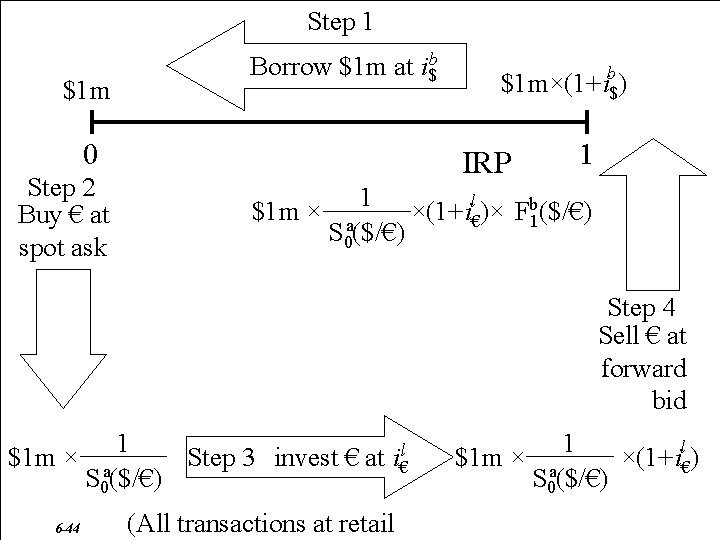
Step 1 $1 m Borrow $1 m at i$b 0 Step 2 Buy € at spot ask $1 m×(1+ib$) IRP 1 1 l $1 m × a ×(1+i€)× Fb 1($/€) S 0($/€) Step 4 Sell € at forward bid 1 Step 3 invest € at i€l $1 m × a S 0($/€) 6 -44 (All transactions at retail 1 $1 m × a ×(1+il€) S 0($/€)


Homework 2, 4, 6, 7, 21, 22
- Slides: 46