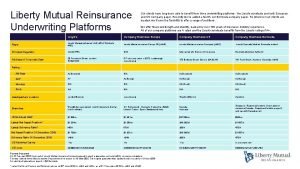
Hidden Risks in Casualty Reinsurance Casualty Actuaries in

Hidden Risks in Casualty (Re)insurance Casualty Actuaries in Reinsurance (CARe) 2007 David R. Clark, Vice President Munich Reinsurance America, Inc.

Agenda Overview of Inflation Risk A Model for Inflation 3 5 Including Inflation Variability in the Collective Risk Model 10 Including Inflation Variability in Portfolio Management 15 2

Hidden Risks in Casualty (Re)insurance Introduction 1) Parameter Risk § Recognize uncertainty in pricing parameters 2) Adverse Selection § Which companies supply their own development patterns? § Which companies need to purchase this type of coverage? 3) Systematic Risks § Inflation We will only cover this item § Market Cycle § Other coverage changes (e. g. , WC reforms) 4) Mega-Risks (the “next asbestos”) 3

Hidden Risks in Casualty (Re)insurance Introduction Key Ideas: § Estimate variability due to inflation using time-series analysis* § Use this variability as a “mixing” distribution § For aggregate ground-up losses § To adjust contagion for excess frequency *Based on Variance and Covariance Due to Inflation, in the Fall 2006 Reserves Call Paper Program 4

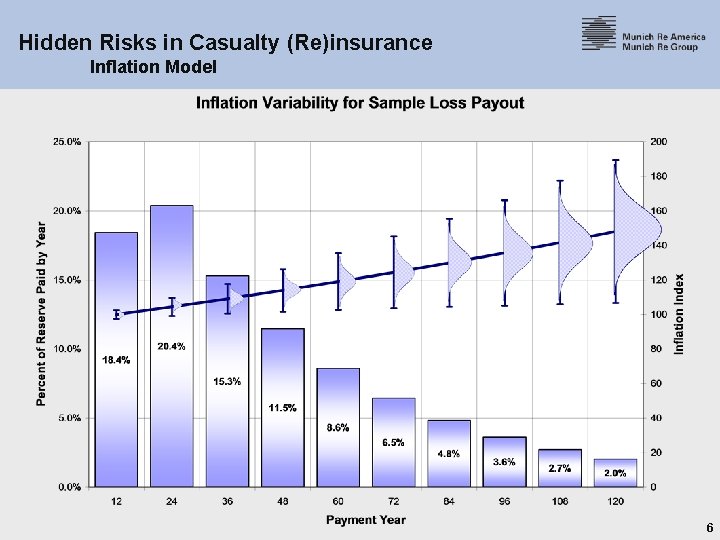
Hidden Risks in Casualty (Re)insurance Inflation Model There are two components to the inflation variability model: 1) An expected pattern of future loss payments § Typically on a quarterly or annual basis 2) The inflation index covering the same time horizon as the payout pattern § Ideally this should be derived from insurance statistics § Practically, it may be based on economic statistics (e. g. , the most relevant CPI) 5

Hidden Risks in Casualty (Re)insurance Inflation Model 6

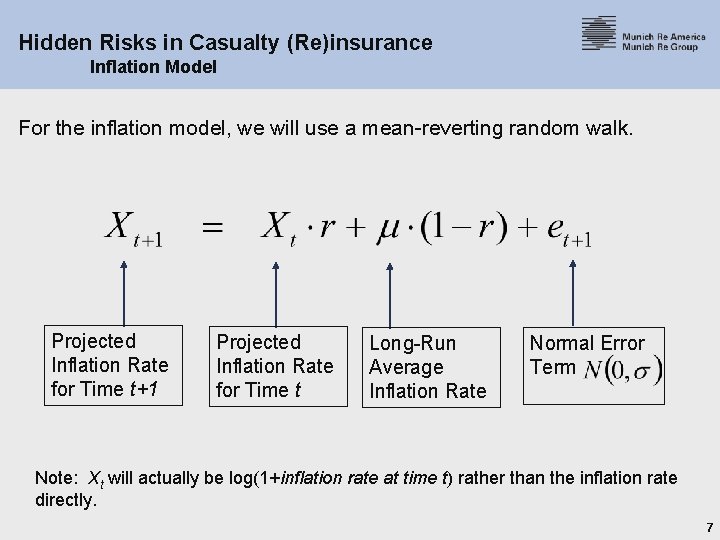
Hidden Risks in Casualty (Re)insurance Inflation Model For the inflation model, we will use a mean-reverting random walk. Projected Inflation Rate for Time t+1 Projected Inflation Rate for Time t Long-Run Average Inflation Rate Normal Error Term Note: Xt will actually be log(1+inflation rate at time t) rather than the inflation rate directly. 7

Hidden Risks in Casualty (Re)insurance Inflation Model § The idea of the mean-reverting random walk is that the inflation rate for one year is dependent on the inflation rate in the immediately prior year, but with a tendency back towards some long-run average rate. § This is sometimes illustrated by a drunk whose every step could be in a different direction, but who has at least a vague idea of how to stagger back home. 8

Hidden Risks in Casualty (Re)insurance Including Inflation in Collective Risk Model Given a model of inflation and an expected payout pattern for losses, we can estimate the variability of the loss amount. This inflation variability is implemented as a “mixing distribution that puts variability around the scale of the severity curve. For the next step, we need to consider the Collective Risk Model, which treats the number of claims (N) and the amount of each individual claim (Xi) as random variables. 9

Hidden Risks in Casualty (Re)insurance Including Inflation in Collective Risk Model Variance formula for the Collective Risk Model: This includes two key independence assumptions: 1) Frequency and severity are independent 2) Each loss (severity) is independent If we also include the correlation between losses, then this formula is expanded for a covariance term: covariance 10

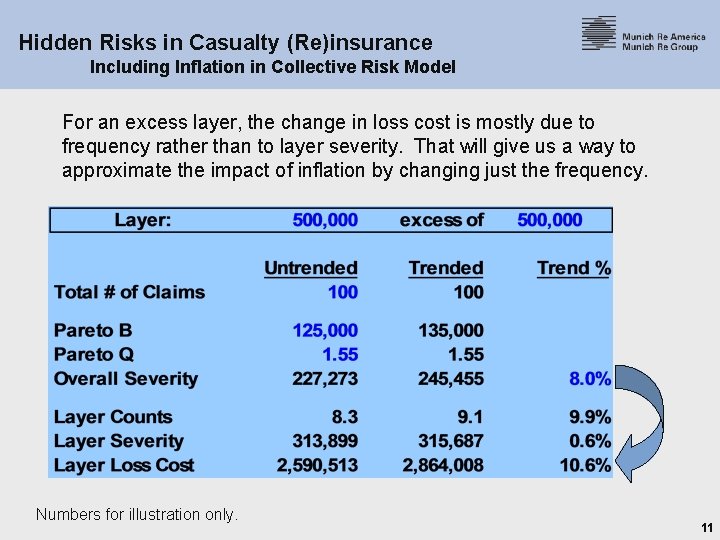
Hidden Risks in Casualty (Re)insurance Including Inflation in Collective Risk Model For an excess layer, the change in loss cost is mostly due to frequency rather than to layer severity. That will give us a way to approximate the impact of inflation by changing just the frequency. Numbers for illustration only. 11

Hidden Risks in Casualty (Re)insurance Including Inflation in Collective Risk Model Variance Formulas for Ground-up (GU) and Excess (XS) Layer Counts: c = “contagion” : constant for all layers p = 1 -F(Att. Pt) = probability of hitting the excess layer 12

Hidden Risks in Casualty (Re)insurance Including Inflation in Collective Risk Model To include variance from inflation in the excess (XS) layer counts, we simply add a term to the “contagion”: c = “contagion” p = 1 -F(Att. Pt) = probability of hitting the excess layer Var(p) = variance in the probability “p” due to inflation 13

Hidden Risks in Casualty (Re)insurance Including Inflation in Collective Risk Model Importance of Contract Terms: § Annual Aggregate Deductibles (AADs) are very sensitive to inflation § Limited Reinstatements can help avoid extreme fluctuations § Some protection comes from policy limits on the underlying subject business § Indexation Clauses are another protection: § Goal is to share inflation risk equitably with the ceding company – inflation risk is tempered but not eliminated § Potential “basis risk” in choosing a base index 14

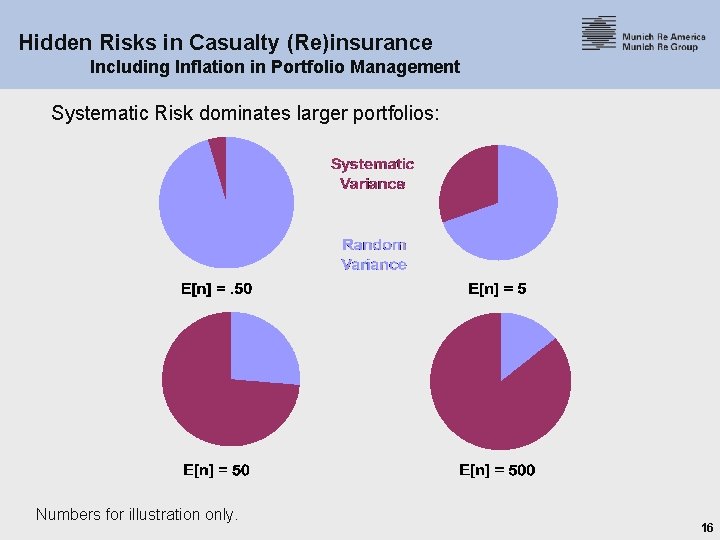
Hidden Risks in Casualty (Re)insurance Including Inflation in Portfolio Management Including Inflation Variability in Portfolio Management: § The impact of inflation on an individual treaty may be small compared to other sources of variability. § Major significance is the systematic impact: inflation will affect much of the portfolio simultaneously. It is not a fully diversifiable risk. § The next graph illustrates that as the portfolio grows, the systematic risk begins to dominate the variability. 15

Hidden Risks in Casualty (Re)insurance Including Inflation in Portfolio Management Systematic Risk dominates larger portfolios: Numbers for illustration only. 16

Hidden Risks in Casualty (Re)insurance Conclusions: § It is possible to estimate the variability from inflation § The biggest impact from this variability is the implied correlation between losses and between treaties – it is a SYSTEMATIC effect § One practical approach is the use of mixing parameters, such as the “contagion“ in the Negative Binomial frequency distribution 17

Thank you very much for your attention. David R. Clark, Vice President Munich Reinsurance America, Inc. © Copyright 2007 Munich Reinsurance America, Inc. All rights reserved. The Munich Re America name is a mark owned by Munich Reinsurance America, Inc. The material in this presentation is provided for your information only, and is not permitted to be further distributed without the express written permission of Munich Reinsurance America. This material is not intended to be legal, underwriting, financial, or any other type of professional advice. Examples given are for illustrative purposes only.