GRADE 10 ACADEMIC MPM 2 D UNIT 5

GRADE 10 ACADEMIC (MPM 2 D) UNIT 5: TRIGONOMETRY APPLICATIONS OF THE TRIGONOMETRIC RATIOS 2 Mr. Choi © 2017 E. Choi – MPM 2 D - All Rights Reserved

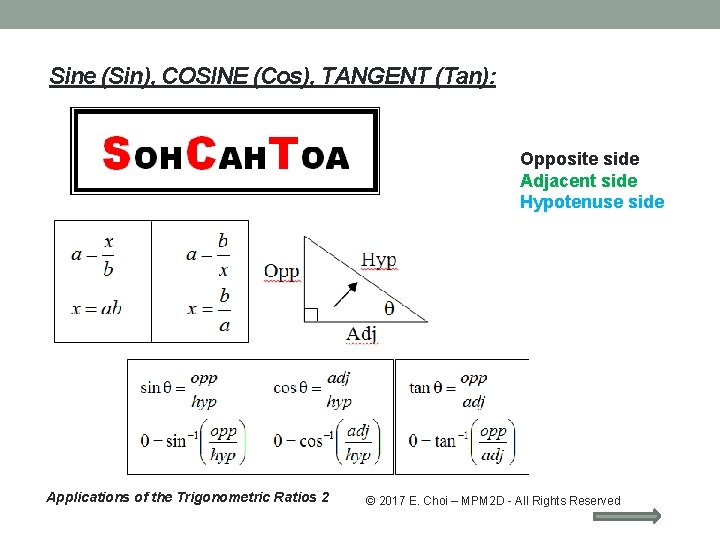
Sine (Sin), COSINE (Cos), TANGENT (Tan): Opposite side Adjacent side Hypotenuse side Applications of the Trigonometric Ratios 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

Solving Right Triangles To solve a right triangle means to find all the unknown sides and unknown angles. It requires that you find the “missing” three pieces of information. As with congruent triangles, if you are given the proper three pieces of information you will draw a unique triangle. The three cases are: Case 1. SIDE-SIDE Triangle Case 2. SIDE-ANGLE-SIDE Triangle Case 3. ANGLE-SIDE-ANGLE Triangle The strategy to solve a right triangle will require: 1. The Pythagorean Theorem 2. The Sum of the Angles in a Triangle Theorem 3. Trigonometry Applications of the Trigonometric Ratios 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

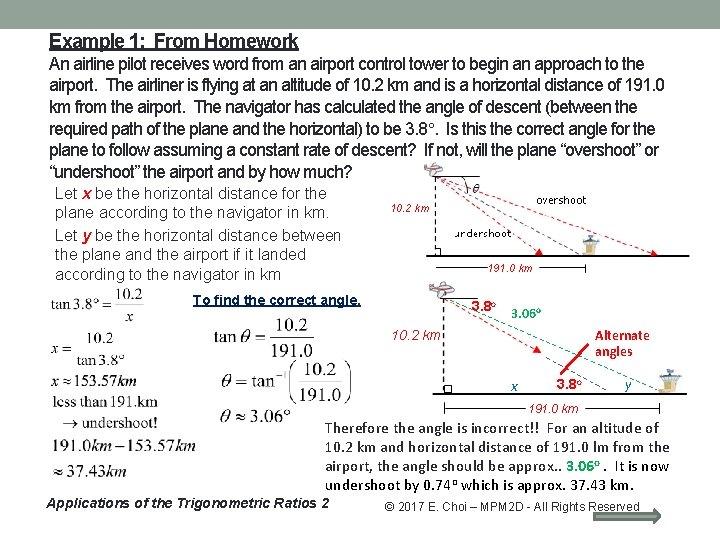
Example 1: From Homework An airline pilot receives word from an airport control tower to begin an approach to the airport. The airliner is flying at an altitude of 10. 2 km and is a horizontal distance of 191. 0 km from the airport. The navigator has calculated the angle of descent (between the required path of the plane and the horizontal) to be 3. 8. Is this the correct angle for the plane to follow assuming a constant rate of descent? If not, will the plane “overshoot” or “undershoot” the airport and by how much? Let x be the horizontal distance for the plane according to the navigator in km. Let y be the horizontal distance between the plane and the airport if it landed according to the navigator in km 10. 2 km 191. 0 km To find the correct angle. 3. 8 o 3. 06 o Alternate angles 10. 2 km x 3. 8 o y 191. 0 km Therefore the angle is incorrect!! For an altitude of 10. 2 km and horizontal distance of 191. 0 lm from the airport, the angle should be approx. . 3. 06 o. It is now undershoot by 0. 74 o which is approx. 37. 43 km. Applications of the Trigonometric Ratios 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 2: From Homework The Great Pyramid of Egypt has a base in the shape of a square with sides having lengths of 230 metres. Each of the four faces makes an angle of 52 with the ground. If you could climb to the top of the pyramid, how far would you climb, to the nearest metre, by the shortest distance? When you reach the top, how far above the ground would you be? Let x be the slanted distance between the midpoint of the side to the top of the pyramid in m. Let h be the height of the pyramid in m. x h 52 o 115 m Therefore the slanted distance between the midpoint of the side to the top of the pyramid is approx. 186. 79 m and the height of the pyramid is approx. 147. 19 m. Applications of the Trigonometric Ratios 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

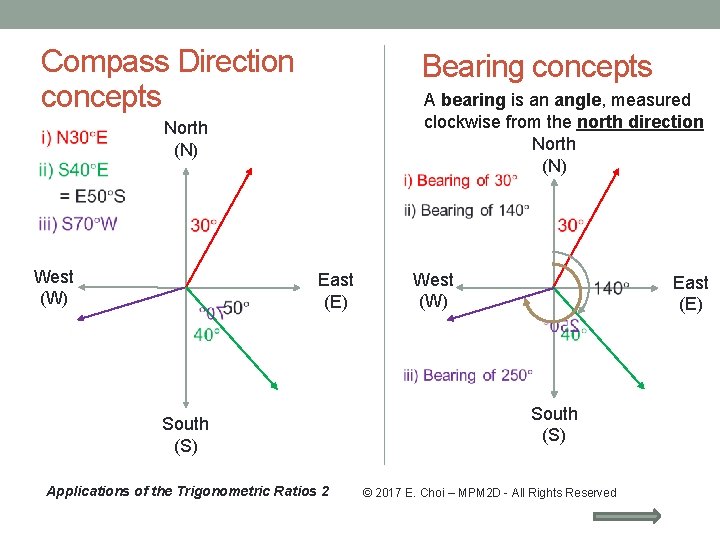
Compass Direction concepts Bearing concepts North (N) West (W) A bearing is an angle, measured clockwise from the north direction North (N) West (W) East (E) South (S) Applications of the Trigonometric Ratios 2 South (S) © 2017 E. Choi – MPM 2 D - All Rights Reserved East (E)

Example 3: A cruise ship is trying to cruise due south. After five hours of travelling, the captain notices that he is actually on a course of S 39 W . If he was traveling at an average speed of 200 km/h, how far “off-course” is he? 5 hours at 200 km/h 1000 km Let w be the off-course distance travelled in km Let x be half of the off-course distance travelled in km (constructed). 5 19 1000 km 39 o 1000 km x N w Therefore the cruise ship is off-course by 667. 61 km after 5 hours. Applications of the Trigonometric Ratios 2 south © 2017 E. Choi – MPM 2 D - All Rights Reserved

Homework Work sheet: Applications of Trigonometric Ratios 2 #1 - 5 Text: P. 509 #3 - 13 Check the website for updates Applications of the Trigonometric Ratios 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

End of lesson Applications of the Trigonometric Ratios 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved