Grade 10 Academic MPM 2 D Unit 6

Grade 10 Academic (MPM 2 D) Unit 6: Trigonometry 2: Non-Right Triangles Cosine Law Mr. Choi © 2017 E. Choi – MPM 2 D - All Rights Reserved

Trigonometry is a branch of mathematics that studies the relationship between the measures of the angles and the lengths of the sides in triangles. Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Notation: In any triangle, the vertices are named using capital letters as in the given example. The lengths of the sides are named using lower case letters that match the opposite vertex. b c a Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

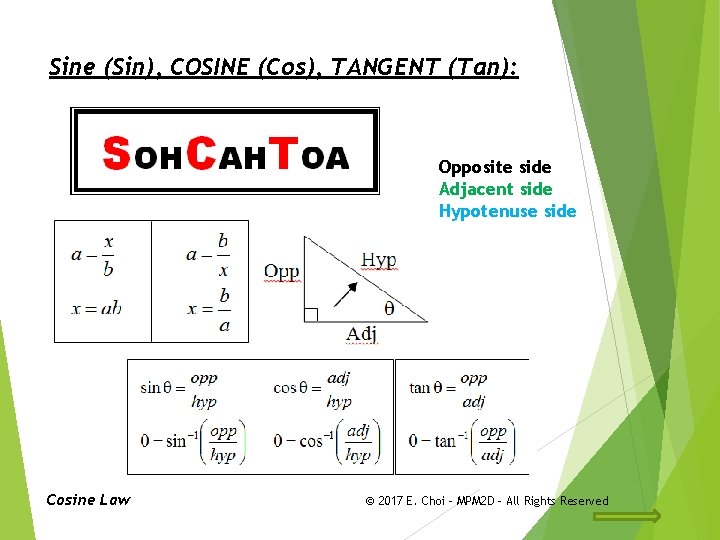
Sine (Sin), COSINE (Cos), TANGENT (Tan): Opposite side Adjacent side Hypotenuse side Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Earlier you explored the relations between the angle measures and sides of right triangles. You developed ratios of the lengths of the sides of similar triangles and called these trigonometric ratios sine, cosine, and tangent. Of course, not all realworld situations can be modelled with right triangles. Other methods must be found to solve problems that involve general, nonright triangles. Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Sine Law or Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Cosine Law a In ADC Cosine Law In ABD © 2017 E. Choi – MPM 2 D - All Rights Reserved

Cosine Law (Technique to memorize!!) Pythagorean component Same __ __ Corresponding side and its angle f e OR d Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Cosine Law Using Cosine Law to find the angles Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 1: Cosine Law (SAS) Solve the triangle ABC if a = 51 cm, B = 39° and c = 42 cm. Cosine Law 42 cm b 39° 51 cm Sine Law Supplementary Angles Reference Ratio Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

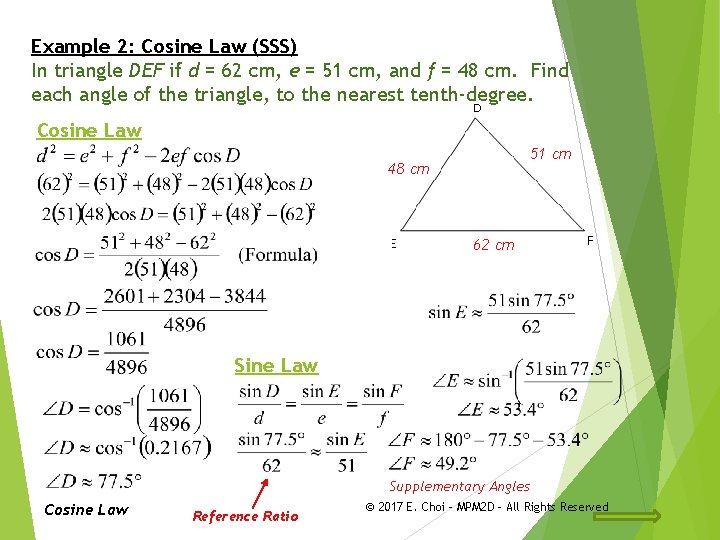
Example 2: Cosine Law (SSS) In triangle DEF if d = 62 cm, e = 51 cm, and f = 48 cm. Find each angle of the triangle, to the nearest tenth-degree. Cosine Law 51 cm 48 cm 62 cm Sine Law Supplementary Angles Cosine Law Reference Ratio © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 3: Cosine Law Peter is 5000 m away from the entrance of a tunnel and 5500 m away from the exit of the tunnel, if the angle from his position to the entrance and exit of the tunnel is 10°, find the length of the tunnel, XY, to the nearest metre. Let Z be Peter’s position X be the entrance of the tunnel. Y be the exit of the tunnel. Cosine Law z 5000 m 5500 m y x 10° Therefore the tunnel is approx. 1042 m long to the nearest metre. Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 4: Method 1 The tops of the solid rocket boosters used to launch the space shuttle are cones of diameter 3. 7 m and slant height 5. 4 m. Find the angle that the curved surface of the cone makes with a diameter, to the nearest tenth of a degree. Let be the angle of the curve surface with the diameter in degree. Cosine Law 5. 4 m 3. 7 m Therefore the angle that the curved surface of the cone makes with a diameter is approx. 70. 0 o. Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 4: Method 2 The tops of the solid rocket boosters used to launch the space shuttle are cones of diameter 3. 7 m and slant height 5. 4 m. Find the angle that the curved surface of the cone makes with a diameter, to the nearest tenth of a degree. Let be the angle of the curve surface with the diameter in m. Trigonometric Ratio 5. 4 m For : Given: Adjacent & Hypotenuse COSINE 1. 85 m 3. 7 m Therefore the angle that the curved surface of the cone makes with a diameter is approx. 70. 0 o. Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

Homework Work sheet: Day 1: Cosine Law Sine and Cosine Law Problems Text: Day 2: P. 566 #2, 4, 5 P. 567 #3, 6 – 10, 14 Check the website for updates Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved

End of lesson Cosine Law © 2017 E. Choi – MPM 2 D - All Rights Reserved