Grade 10 Academic MPM 2 D Unit 2













- Slides: 17

Grade 10 Academic (MPM 2 D) Unit 2: Analytic Geometry – Word Problems 2 Mr. Choi © 2017 E. Choi – MPM 2 D - All Rights Reserved

Properties of Triangles Medians: Midpoint: Altitude: Perpendicular bisectors: Angle bisectors: Centroid: Orthocentre: Circumcentre: Incentre: line from vertex to the midpoint of the opposite side point on a line that divides it into 2 equal parts to draw a median find mid point of opposite side and connect to vertex shows the height of a polygon to draw an altitude line from vertex to opposite side so that it meets at 90° perpendicular to a line segment and meets at its midpoint. to draw a perpendicular bisector find midpoint, then measure a right angle, draw line. The (interior) bisector of an angle, also called the internal angle bisector is the line or line segment that divides the angle into two equal parts where all 3 medians meet divides each median in the ratio 1: 2 it is the centre of mass where all 3 altitudes meet where all 3 perpendicular bisectors meet centre of the circle that passes through the vertices of the triangle the circle is called circumcircle or circumscribed circle where all 3 angle bisectors meet centre of the circle that meets each side once the circle is called incircle or inscribed circle Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

Quadrilaterals If you know the coordinates of the vertices of a quadrilateral, You can determine the length and slopes of the sides and use the information to classify the quadrilateral as - Parallelogram (both pairs of opposite sides are parallel), - Rectangle (parallelogram and adjacent sides are perpendicular), - Square (rectangle and all sides are same length), - Rhombus (both pairs of opposite sides are parallel and all sides are the same length). Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

When triangles and quadrilaterals are drawn on a coordinate plane, they are constructed from line segments. The lengths and slopes of the line segments can be used to classify or define specific types of triangles and quadrilaterals. Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 The plan shows the positions of three entrances to a parking lot. A tall mast light is to be erected to illuminate three entrances, A (-8, 14), B (-4, 8), and C (18, 10). a) Where should the light be located to illuminate each entrance equally? b) If the closest power line to the parking lot runs along a straight line containing points (0, 4) and (12, 10). At what point should the lighting contractors connect to the power line, and how much cable will they need to reach the lamp? Each unit on the plan equals to 1 m. Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 The plan shows the positions of three entrances to a parking lot. A tall mast light is to be erected to illuminate three entrances, A (-8, 14), B (-4, 8), and C (18, 10). a) Where should the light be located to illuminate each entrance equally? Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

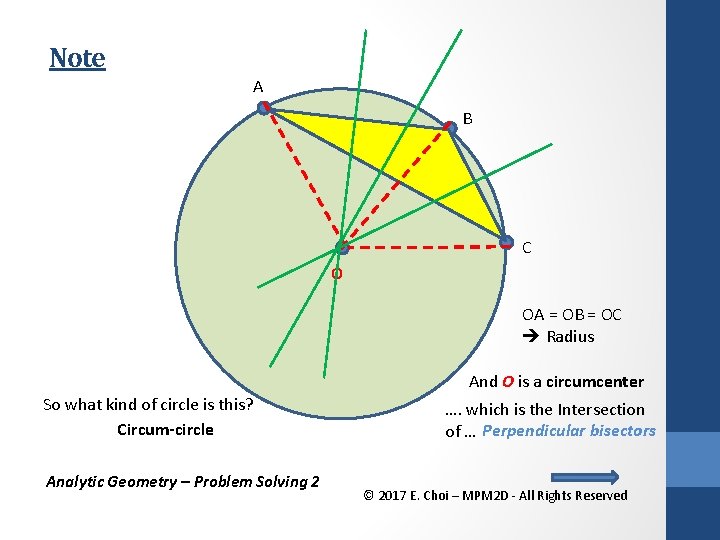
Note A B C O OA = OB = OC Radius And O is a circumcenter So what kind of circle is this? Circum-circle Analytic Geometry – Problem Solving 2 …. which is the Intersection of … Perpendicular bisectors © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 - Perpendicular Bisector of AB a) Where should the light be located to illuminate each entrance equally? For AB: A (-8, 14) B (-4, 8) Midpoint: Substitute midpoint (-6, 11) The light should be located the same distance from each entrance. This point is the centre of the circle that contains the three entrance points circumcentre Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

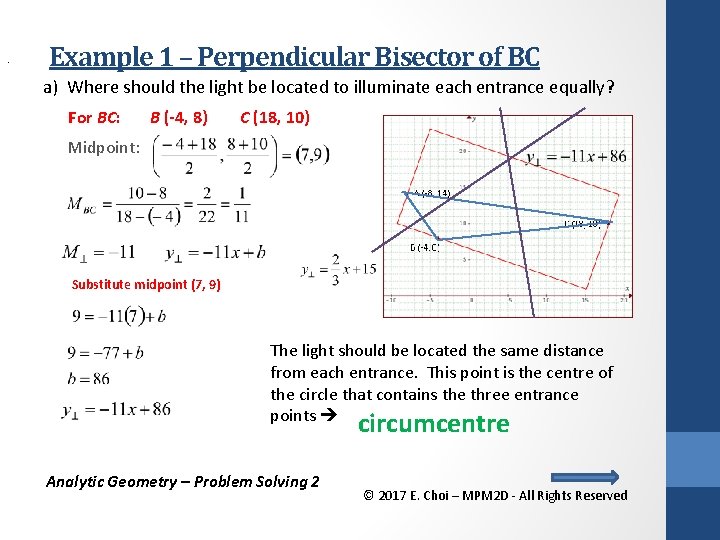
. Example 1 – Perpendicular Bisector of BC a) Where should the light be located to illuminate each entrance equally? For BC: B (-4, 8) C (18, 10) Midpoint: Substitute midpoint (7, 9) The light should be located the same distance from each entrance. This point is the centre of the circle that contains the three entrance points circumcentre Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

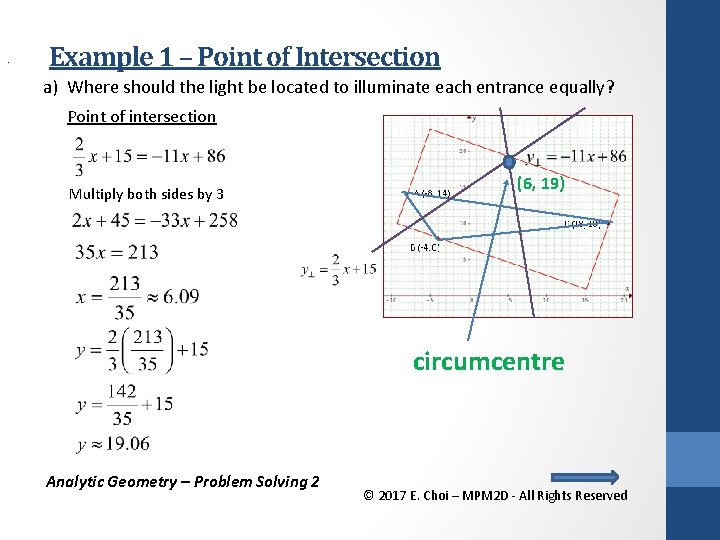
. Example 1 – Point of Intersection a) Where should the light be located to illuminate each entrance equally? Point of intersection Multiply both sides by 3 (6, 19) circumcentre Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

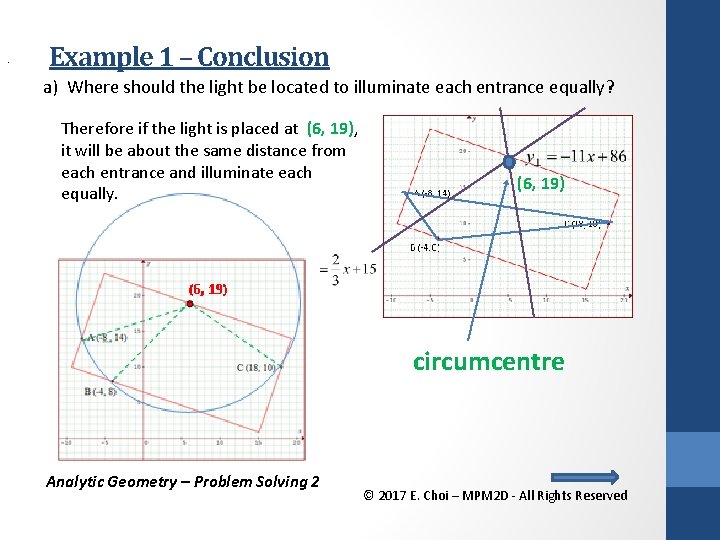
. Example 1 – Conclusion a) Where should the light be located to illuminate each entrance equally? Therefore if the light is placed at (6, 19), it will be about the same distance from each entrance and illuminate each equally. (6, 19) circumcentre Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 b b) If the closest power line to the parking lot runs along a straight line containing points (0, 4) and (12, 10). At what point should the lighting contractors connect to the power line, and how much cable will they need to reach the lamp? Each unit on the plan equals to 1 m. Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 b: Equation of the Power line Recall: The light is at (6, 19). The shortest distance from the light to the power line is the perpendicular distance shown in the sketch. You want to find the point of intersection of the power line and the perpendicular line from (6, 19). Power line points: (0, 4) & (12, 10) Find the equations of the lines that contain these two line segments. The slope of the power line is: (6, 19) (12, 10) (0, 4) The y – intercept is at (0, 4). The equation of the power line is Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 b: Shortest Distance Equation Recall: The light is at (6, 19). The shortest distance from the light to the power line is the perpendicular distance shown in the sketch. Recall: Power line is: (6, 19) Use the point (6, 19) (12, 10) At the point where the perpendicular from (6, 19) meets the power line, Multiply both sides by 2 Analytic Geometry – Problem Solving 2 (10. 8, 9. 4) (0, 4) Therefore the contractor should connect into the power line at point (10. 8, 9. 4). © 2017 E. Choi – MPM 2 D - All Rights Reserved

. Example 1 b: Distance Recall: The light is at (6, 19). The shortest distance from the light to the power line is the perpendicular distance shown in the sketch. Recall: M (6, 19) The length of the cable required: M(6, 19) D (10. 8, 9. 4) (12, 10) D (10. 8, 9. 4) (0, 4) Therefore the contractor will need about 10. 7 m of cable to connect the light to the power line. Recall: 1 unit = 1 m Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

Homework Work sheet: Day 1: #1 – 13 (odd) Day 2: Even Text: • Day 1 P 182 #2, 3, 5 — 10 P 183 #11 odd, 13, 17 a, 18, 20 • Day 2 Read P. 200 Examples 1 & 2 P 196 #22 P 203 #3— 7, 10, 11 • Check the website for updates Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved

End of lesson Analytic Geometry – Problem Solving 2 © 2017 E. Choi – MPM 2 D - All Rights Reserved
 Logo mpm
Logo mpm Cpm mpm
Cpm mpm Mpm3606a
Mpm3606a Sukatan pelajaran sejarah stpm penggal 1 2020
Sukatan pelajaran sejarah stpm penggal 1 2020 Mpm manufacturing process management
Mpm manufacturing process management Flowatch subsea
Flowatch subsea Mpm degree
Mpm degree Mod bus mpm
Mod bus mpm Map of canada grade 9
Map of canada grade 9 2nd grade academic vocabulary
2nd grade academic vocabulary Spse essay sample
Spse essay sample Unit 10, unit 10 review tests, unit 10 general test
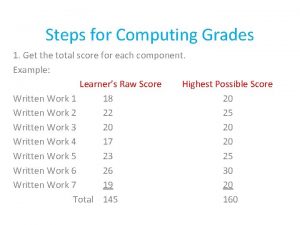
Unit 10, unit 10 review tests, unit 10 general test What are the steps in computing grades
What are the steps in computing grades Cinderella dressed in yellow game
Cinderella dressed in yellow game Culinary
Culinary Grade a vs grade b milk
Grade a vs grade b milk Grade grade
Grade grade Meta - change morph
Meta - change morph