GRADE 10 ACADEMIC MPM 2 D UNIT 5

Trigonometry is a branch of mathematics that studies the relationship between the measures of

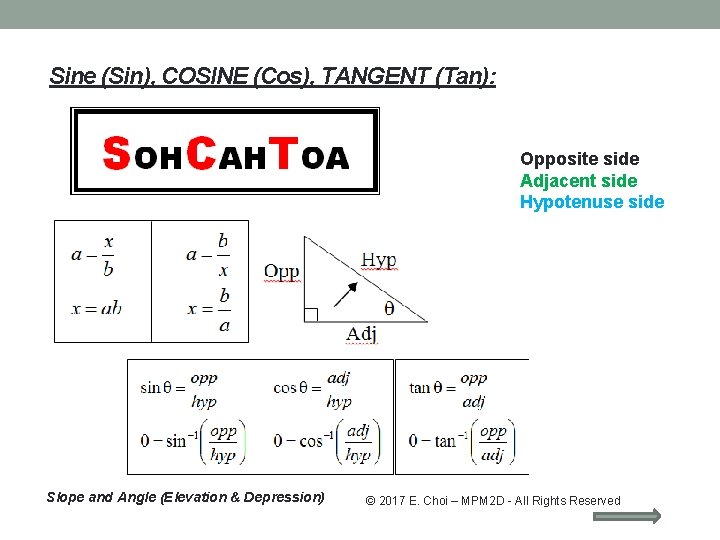
Sine (Sin), COSINE (Cos), TANGENT (Tan): Opposite side Adjacent side Hypotenuse side Slope and

Slope and Slope Angles Slope of a line is given by ratio The slope

Angle of Elevation & Angle of Depression When the line rises above the horizontal,

Example 1: Find to the nearest degree, the angle of inclination of a ramp

Example 2 a: Find the slope angle for the line with equation TANGENT Slope

Example 2 b: Find the slope angle for the line with equation y x

Example 3: Esther starts her mountain hike from a point 600 m above the

Example 4: Find the height of a flagpole that casts a shadow 18. 6

Example 5: From an airplane 420 m above the ground, the angle of depression

Example 6: (Double Tangent Problem) From a point on the ground, a student sights

Example 6: Double Tangent Problem (Decimal Version) From a point on the ground, a

Homework Work sheet: Text: • P. 485 #2, 4 -7 • P. 498 #14,

End of lesson Slope and Angle (Elevation & Depression) © 2017 E. Choi –

Slides: 15

Download presentation

Trigonometry is a branch of mathematics that studies the relationship between the measures of the angles and the lengths of the sides in triangles. Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

Slope and Slope Angles Slope of a line is given by ratio The slope is related to the angle the line makes with the x-axis, which is called the slope-angle. Parallel lines have equal slopes and equal slope-angles. Lines with a positive slope have slope-angle between 0 o and 90 o. Lines with a negative slope have slope-angle between -90 o and 0 o. If it is “-“, it can be expressed as an equivalent angle between 90 o and 180 o using the expression (slope-angle) + 180 o. Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

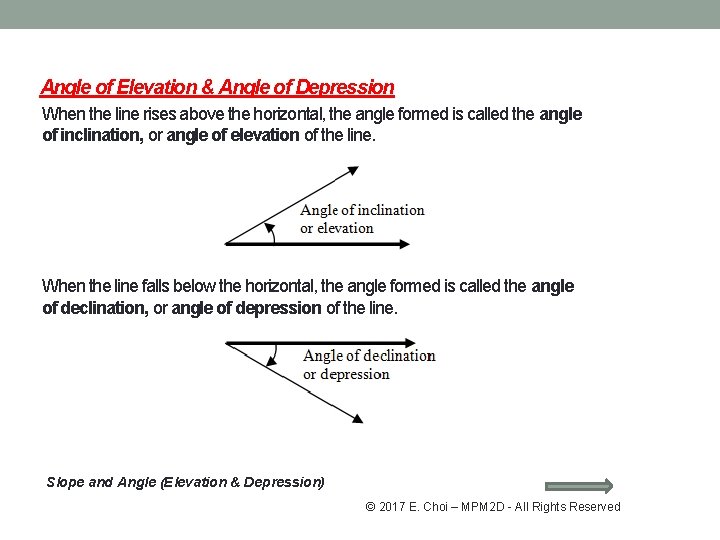
Angle of Elevation & Angle of Depression When the line rises above the horizontal, the angle formed is called the angle of inclination, or angle of elevation of the line. When the line falls below the horizontal, the angle formed is called the angle of declination, or angle of depression of the line. Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 2 b: Find the slope angle for the line with equation y x TANGENT Lines with a negative slope have slopeangle between -90 o and 0 o. If it is “-“, it can be expressed as an equivalent angle between 90 o and 180 o using the expression (slope-angle) + 180 o. Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

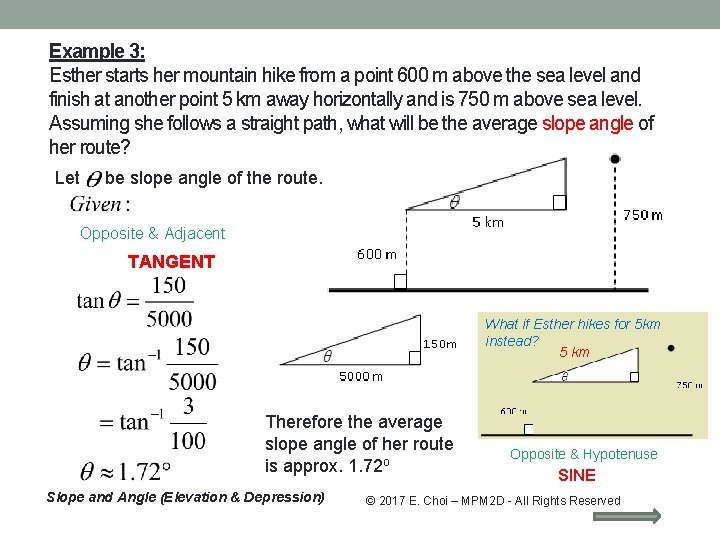
Example 3: Esther starts her mountain hike from a point 600 m above the sea level and finish at another point 5 km away horizontally and is 750 m above sea level. Assuming she follows a straight path, what will be the average slope angle of her route? Let be slope angle of the route. Opposite & Adjacent TANGENT What if Esther hikes for 5 km instead? 5 km Therefore the average slope angle of her route is approx. 1. 72 o Slope and Angle (Elevation & Depression) Opposite & Hypotenuse SINE © 2017 E. Choi – MPM 2 D - All Rights Reserved

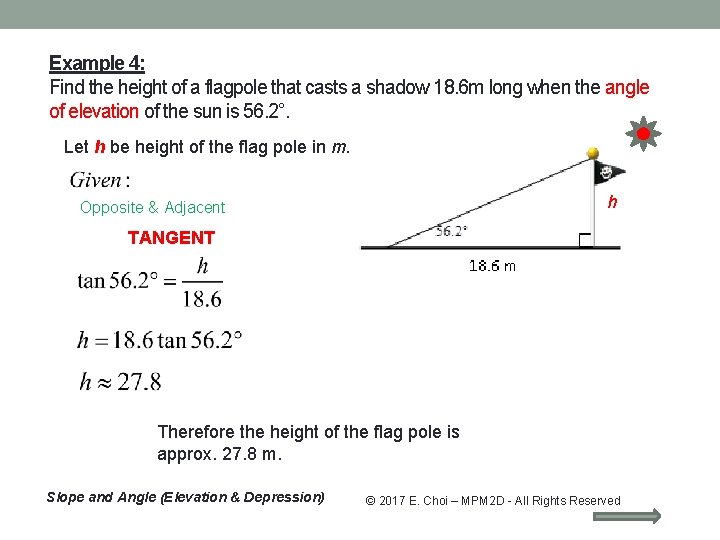
Example 4: Find the height of a flagpole that casts a shadow 18. 6 m long when the angle of elevation of the sun is 56. 2°. Let h be height of the flag pole in m. h Opposite & Adjacent TANGENT Therefore the height of the flag pole is approx. 27. 8 m. Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

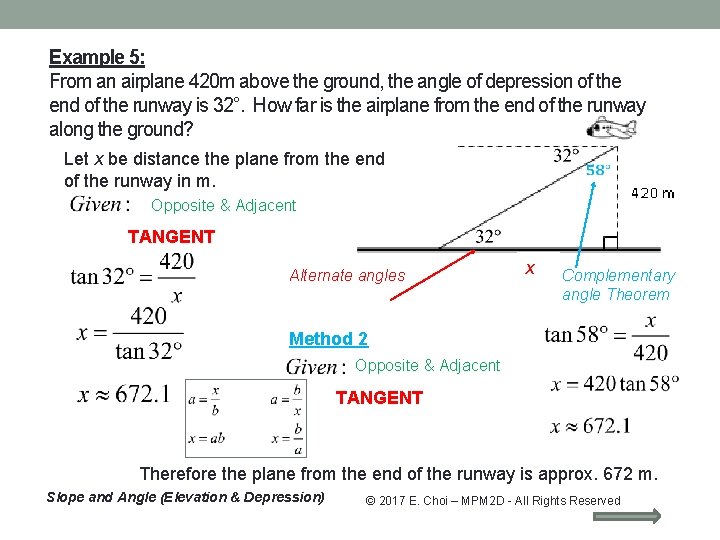
Example 5: From an airplane 420 m above the ground, the angle of depression of the end of the runway is 32°. How far is the airplane from the end of the runway along the ground? Let x be distance the plane from the end of the runway in m. Opposite & Adjacent TANGENT Alternate angles x Complementary angle Theorem Method 2 Opposite & Adjacent TANGENT Therefore the plane from the end of the runway is approx. 672 m. Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 6: (Double Tangent Problem) From a point on the ground, a student sights the top and bottom of a 15 m flagpole on top of a building. The two angles of elevation are 64. 6° and 57. 3°. How far is the student from the foot of the building? Let x be distance between the point and the building in m Let h be the height of the building in m Therefore the distance from the point to the building is approx. 27. 4 m Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved

Example 6: Double Tangent Problem (Decimal Version) From a point on the ground, a student sights the top and bottom of a 15 m flagpole on top of a building. The two angles of elevation are 64. 6° and 57. 3°. How far is the student from the foot of the building? Let x be distance between the point and the building in m Let h be the height of the building in m Therefore the distance from the point to the building is approx. 27. 4 m Slope and Angle (Elevation & Depression) © 2017 E. Choi – MPM 2 D - All Rights Reserved