GERBEROV NOSA SLOENI NOSAI SA ZGLOBOVIMA GERBEROV NOSA

GERBEROV NOSAČ SLOŽENI NOSAČI SA ZGLOBOVIMA
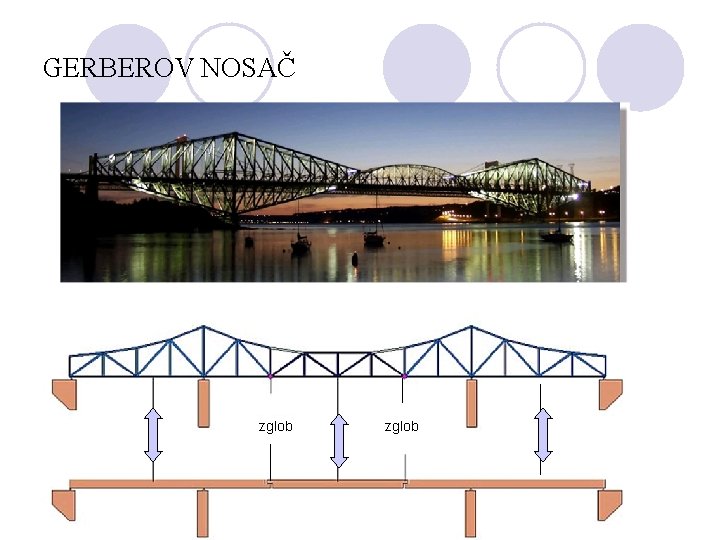
GERBEROV NOSAČ zglob

GERBEROV NOSAČ Statički sustavi gerberovog nosača. To su statički određeni nosači. Najviše se koriste u mostogradnji, ali i u visokogradnji. Izvode se kao: -punostijeni gerberovi nosači -rešetkasti gerberovi nosači

GERBEROV NOSAČ gerberov nosač sastavljeni nosač kontinuirani nosač Slični su kontinuiranim nosačima (st. neodređenim). Kada se predviđaju slijeganje oslonaca i promjene temperature gerberovi nosači su bolje rješenje jer ne nastaju dodatne sile od istoga –to su svojstva statički određenih nosača. Kontinuirani nosači imaju rezerve u pogledu stabilnosti.
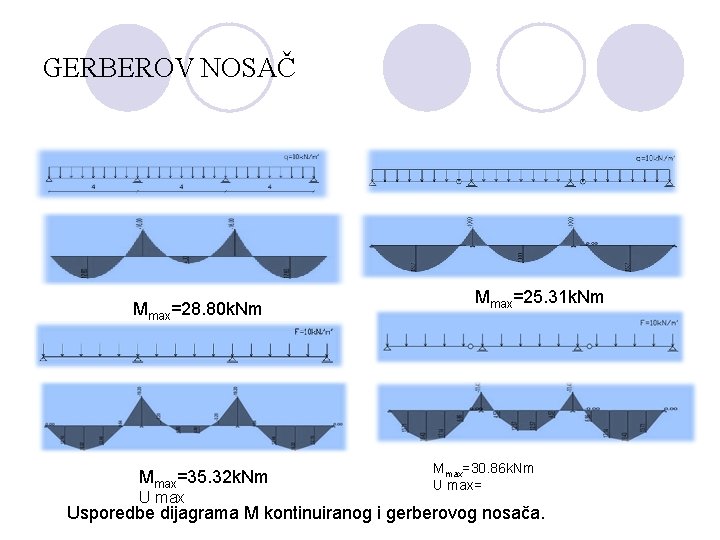
GERBEROV NOSAČ Mmax=28. 80 k. Nm Mmax=35. 32 k. Nm U max Mmax=25. 31 k. Nm Mmax=30. 86 k. Nm U max= Usporedbe dijagrama M kontinuiranog i gerberovog nosača.

GERBEROV NOSAČ PRAVILA FORMIRANJA SUSTAVA Raspored zglobova-ima utjecaj na geometrijsku nepromjenjivost. Mora se voditi računa o pravilnom rasporedu istih. S=0 U jednom polju ne smiju biti 3 zgloba. U dva susjedna polja ne smiju biti 2 zgloba.
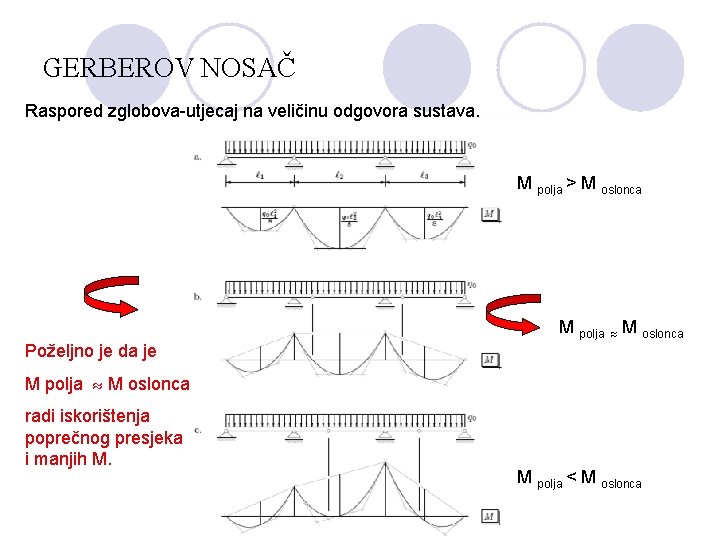
GERBEROV NOSAČ Raspored zglobova-utjecaj na veličinu odgovora sustava. M polja > M oslonca M polja M oslonca Poželjno je da je M polja M oslonca radi iskorištenja poprečnog presjeka i manjih M. M polja < M oslonca
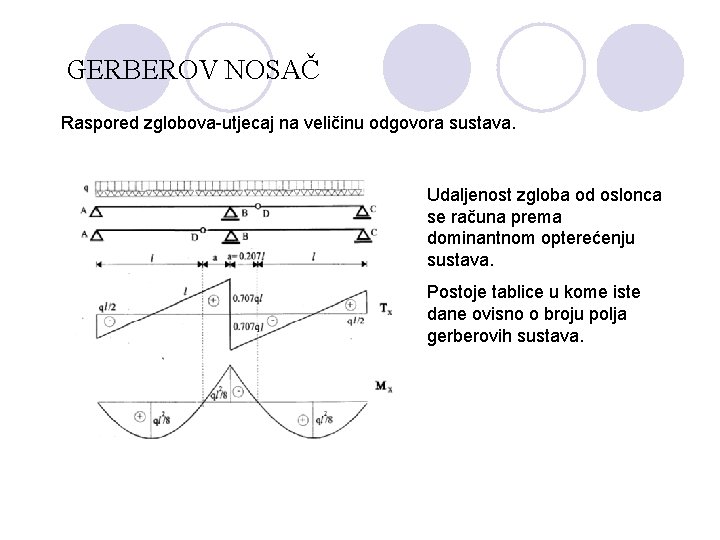
GERBEROV NOSAČ Raspored zglobova-utjecaj na veličinu odgovora sustava. Udaljenost zgloba od oslonca se računa prema dominantnom opterećenju sustava. Postoje tablice u kome iste dane ovisno o broju polja gerberovih sustava.
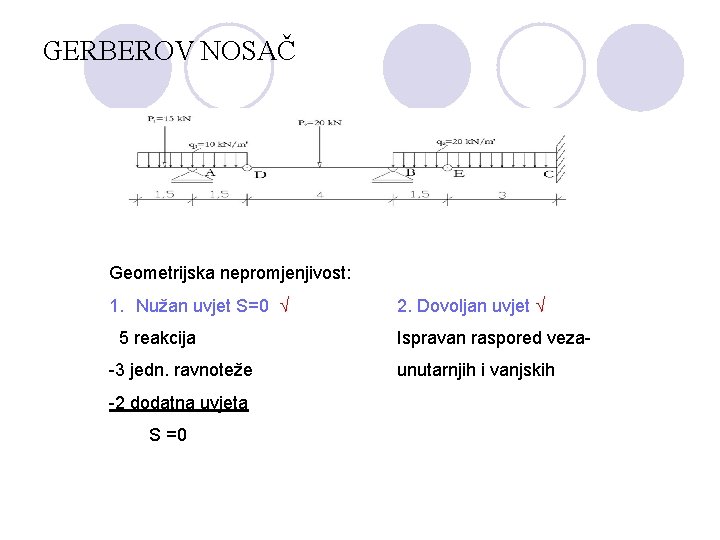
GERBEROV NOSAČ Geometrijska nepromjenjivost: 1. Nužan uvjet S=0 5 reakcija -3 jedn. ravnoteže -2 dodatna uvjeta S =0 2. Dovoljan uvjet Ispravan raspored vezaunutarnjih i vanjskih

GERBEROV NOSAČ Metode rješavanja nepoznatih veličina: l ANALITIČKA METODA: neraščlanjena l GRAFIČKA METODA: za cijeli nosač po poljima l GRAFOANALITIČKA METODA l NUMERIČKA METODA
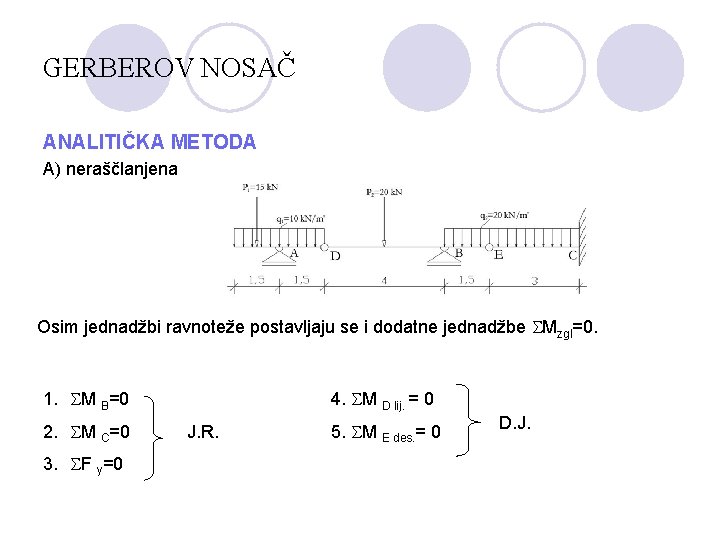
GERBEROV NOSAČ ANALITIČKA METODA A) neraščlanjena Osim jednadžbi ravnoteže postavljaju se i dodatne jednadžbe Mzgl=0. 1. M B=0 2. M C=0 3. F y=0 4. M D lij. = 0 J. R. 5. M E des. = 0 D. J.

GERBEROV NOSAČ ANALITIČKA METODA B) raščlanjena Nosač rastavljamo u zglobovima na elemente vodeći računa o redosljedu naslanjanja elemenata. Zglob na jednom nosaču kao privremeni oslonac, a njegova reakcija kao opterećenje na drugom nosaču.
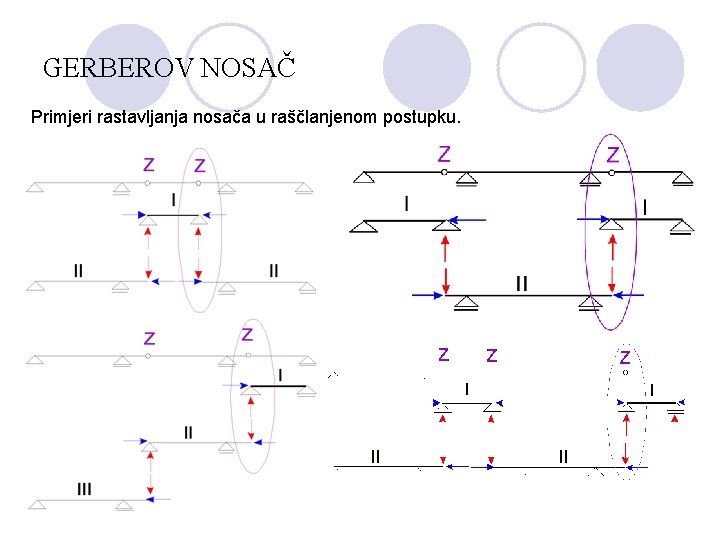
GERBEROV NOSAČ Primjeri rastavljanja nosača u raščlanjenom postupku.
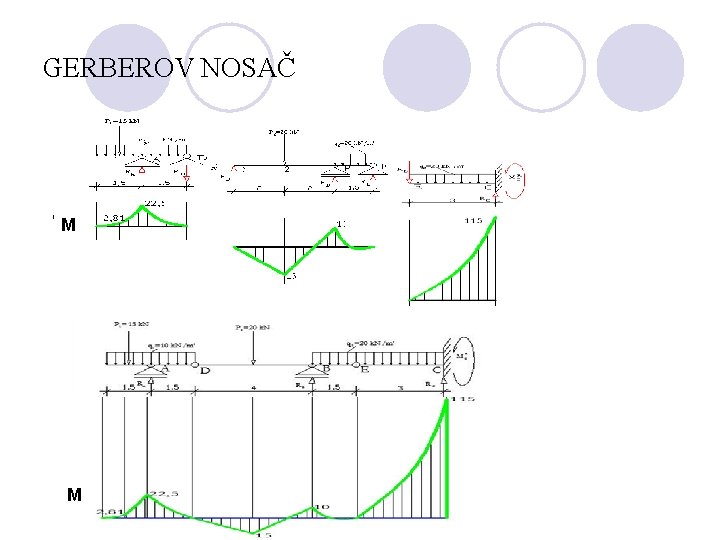
GERBEROV NOSAČ M M
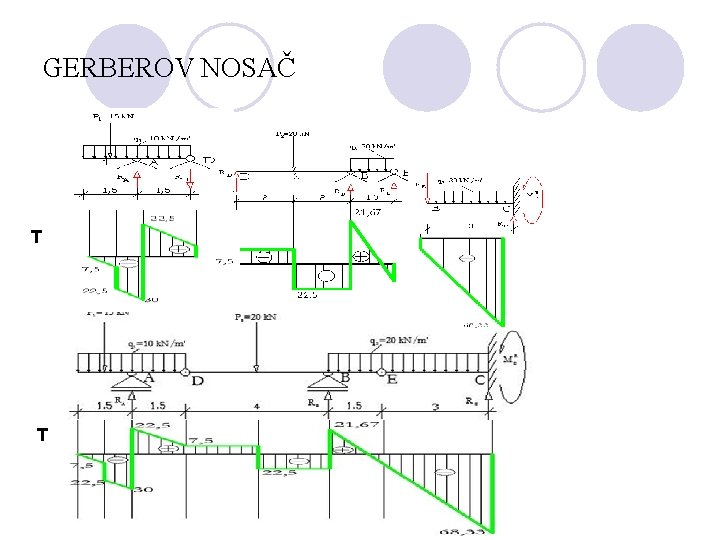
GERBEROV NOSAČ T T T

GERBEROV NOSAČ GRAFIČKA METODA -poligon sila po poljima i verižni poligon (točniji post. ) -jedinstveni poligon sila i verižni poligon
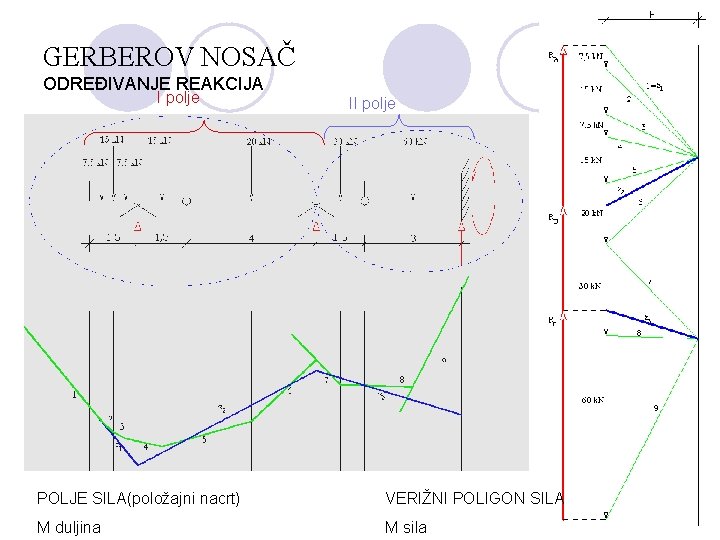
GERBEROV NOSAČ ODREĐIVANJE REAKCIJA I polje II polje POLJE SILA(položajni nacrt) VERIŽNI POLIGON SILA M duljina M sila
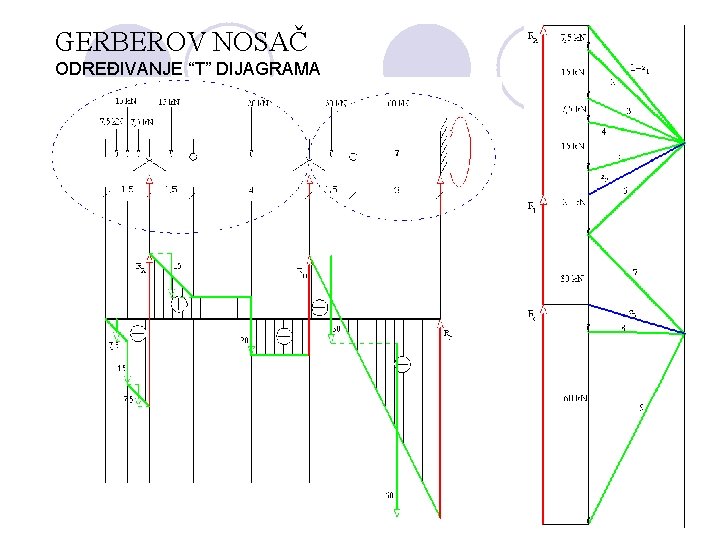
GERBEROV NOSAČ ODREĐIVANJE “T” DIJAGRAMA
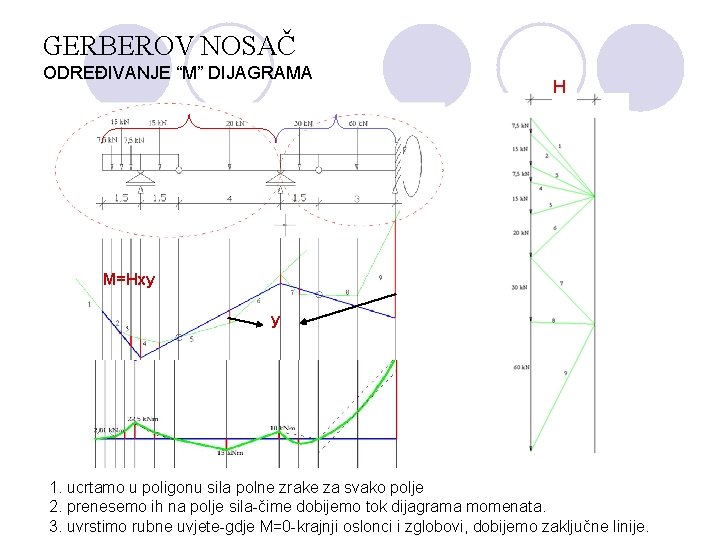
GERBEROV NOSAČ ODREĐIVANJE “M” DIJAGRAMA H M=Hxy y 1. ucrtamo u poligonu sila polne zrake za svako polje 2. prenesemo ih na polje sila-čime dobijemo tok dijagrama momenata. 3. uvrstimo rubne uvjete-gdje M=0 -krajnji oslonci i zglobovi, dobijemo zaključne linije.
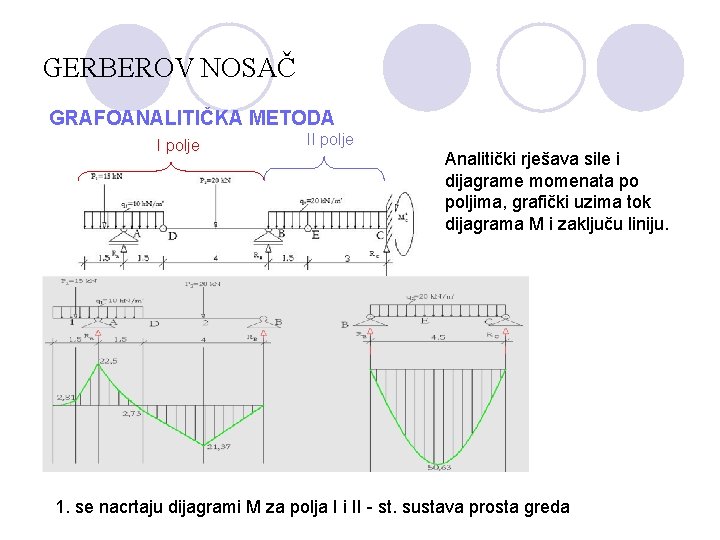
GERBEROV NOSAČ GRAFOANALITIČKA METODA I polje II polje Analitički rješava sile i dijagrame momenata po poljima, grafički uzima tok dijagrama M i zaključu liniju. 1. se nacrtaju dijagrami M za polja I i II - st. sustava prosta greda
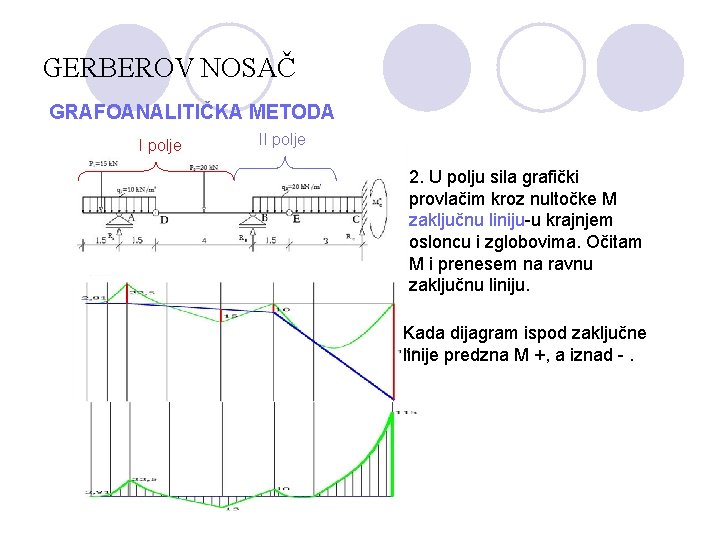
GERBEROV NOSAČ GRAFOANALITIČKA METODA I polje II polje 2. U polju sila grafički provlačim kroz nultočke M zaključnu liniju-u krajnjem osloncu i zglobovima. Očitam M i prenesem na ravnu zaključnu liniju. Kada dijagram ispod zaključne linije predzna M +, a iznad -.
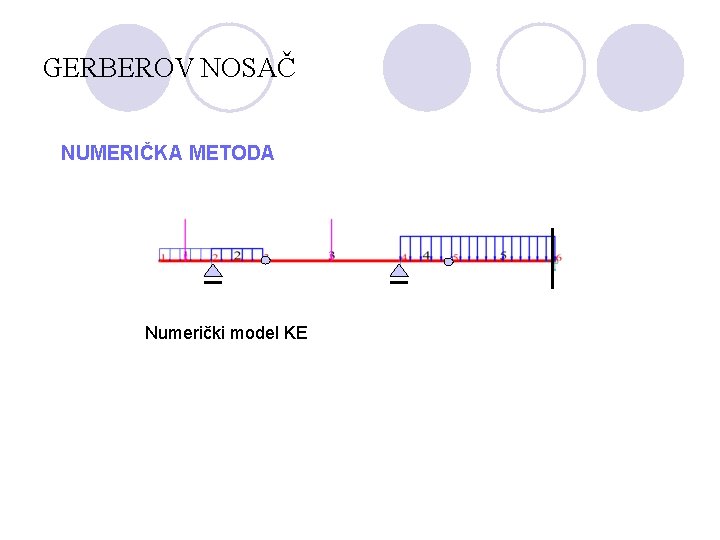
GERBEROV NOSAČ NUMERIČKA METODA Numerički model KE
- Slides: 22