GEM 341 E Ship Hydrodynamics STANBUL TEKNK NVERSTES

GEM 341 E Ship Hydrodynamics İSTANBUL TEKNİK ÜNİVERSİTESİ Naval Architecture and Marine Engineering – B. S. GEM 341 E SHIP HYDRODYNAMICS (Resistance) http: //ninova. itu. edu. tr/Ders/2786 ________________________ 2015 -16 Ö. Gören 1/4

GEM 341 E Ship Hydrodynamics Introduction Ship Hydrodynamics: Resistance of Ships and Ship Propulsion Resistance 1870 ; W. Froude’s attempts are crucial in understanding the components of ship resistance to water (fluid) when moving with a constant velocity 1898 ; J. H. Michell who calculate wave resistance of a thin ship by theoretical analysis 1904 ; L. Prandtl pointed out a viscous layer (boundary layer) near solid surfaces and introduced theory of boundary layer ________________________ 2015 -16 Ö. Gören 2/4

GEM 341 E Ship Hydrodynamics Propulsion 1865 ; W. J. M. Rankine developed momentum theory to calculate thrust generated by a propeller The role of Naval Architect and Marine Engineer within the context of Ship Resistance and Propulsion: i) calculate the resistance and corresponding effective power ( PE = R V), ii) reduce the resistance by means of hull form optimization and by careful design of appendages, sophisticated coatings etc. , iii) optimum choice of propeller dimensions (propeller design), iv) study of the propeller-hull interaction, determine the wake, thrust deduction and hull efficiency, which results in overall propulsive efficiency which yields delivered power PD=PE/ηD v) right choice of suitable machinery with low emissions qualities. ________________________ 2015 -16 Ö. Gören 3/4

GEM 341 E Ship Hydrodynamics Dimensional Analysis The physical problems that we deal with (in hydrodynamics) have always three fundamental units: mass (M), length (L), and time (T). Let Q be the unknown quantity which depends on n-1 significant parameters. In this case there will be n dimensional quantities including Q. According to Buckingham’s Pi Theorem, by taking three fundamental units (M, L, T) into account; nondimensionalization reduce the number n to a total of n-3 nondimensional quantities interrelated. ________________________ 2015 -16 Ö. Gören 4/4

GEM 341 E Ship Hydrodynamics Components of Ship Resistance Dimensional Analysis of a moving body on the free surface implied that non-dimensional resistance (coefficient) should be a function of Froude’s number and Reynolds’ number. Most probably this leads W. Froude – depending also on his extensive set of experiments – to arrive at his hypothesis which states that total resistance can be decomposed into two parts: ________________________ 2015 -16 Ö. Gören 5/8

GEM 341 E Ship Hydrodynamics If we ignore free surface effects (which means no wavemaking in this case), the resultant drag comes from the viscous effects. Viscous effects cause viscous forces which are due to the tangential shear stress (τ) and normal stess (p; viscous pressure). τ p Integration of shear stress and viscous pressure over the body gives, respectively, the frictional resistance and viscous pressure drag. ________________________ 2015 -16 Ö. Gören 6/8

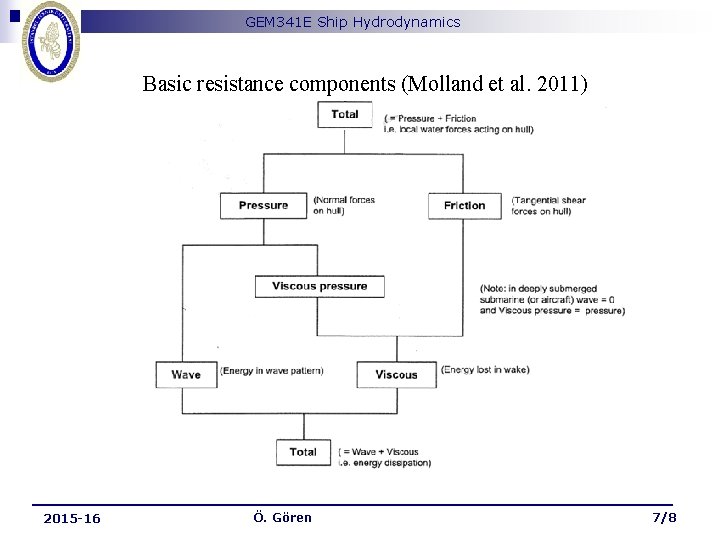
GEM 341 E Ship Hydrodynamics Basic resistance components (Molland et al. 2011) ________________________ 2015 -16 Ö. Gören 7/8

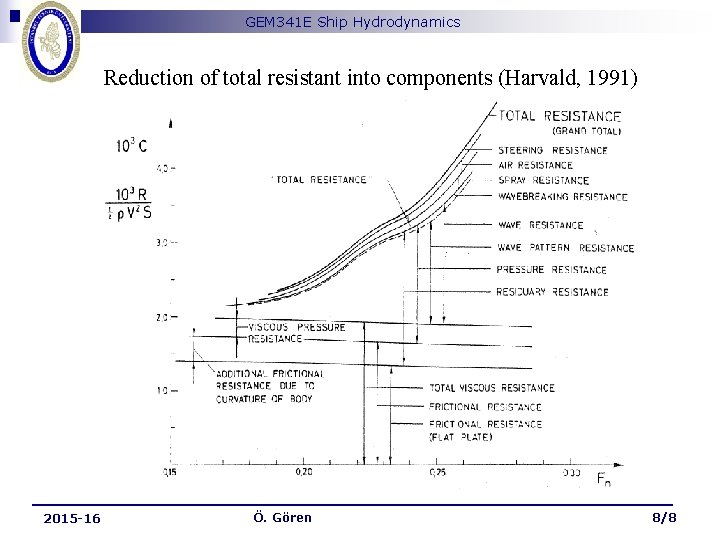
GEM 341 E Ship Hydrodynamics Reduction of total resistant into components (Harvald, 1991) ________________________ 2015 -16 Ö. Gören 8/8