Game Theory Dr Jennifer P Wissink 2011 John

Game Theory Dr. Jennifer P. Wissink © 2011 John M. Abowd and Jennifer P. Wissink, all rights reserved.

The Prisoners’ Dilemma Game (Dominant Strategy Equilibrium) u u Roger and Chris have been accused of a crime, which they did commit. They are held in isolated cells and offered the choice of confessing or not. The payoff matrix shows the number of years of prison Roger (the row player) and Chris (the column player) will receive depending upon who confesses and who lies as (Roger’s time, Chris’ time). The game is played one-shot, simultaneously and non-cooperatively.

The Prisoners’ Dilemma: Solution u Roger’s best response (shown in yellow): – If Chris lies, then Roger should confess (Roger gets 0 years of jail, which is better than 1 year in jail). – If Chris confesses, then Roger should confess (Roger gets 5 years of jail, which is better than 6 years in the slammer). u Chris’s best response (shown in green): – If Roger lies, then Chris should confess (Chris gets 0 years of jail). – If Roger confesses, then Chris should confess (Chris gets 5 years of jail).

The Prisoners’ Dilemma: Solution u There is a single dominant strategy equilibrium: – Roger confesses and Chris confesses. – They both go to jail for 5 years. u u The table shows that the dominant strategy is also the Nash equilibrium for this game. Only the payoff (-5, -5) has both a yellow and a green highlight—indicating that it is the best response for both players, given what the other is doing.

The Prisoners’ Dilemma Is Very Distressing. . . , Or Is It? u u u In the Prisoners’ Dilemma game, the “superior” outcome is that both prisoners lie – but that requires cooperation. When the game is only played once, simultaneously and noncooperatively, (confess, confess) is the dominant strategy equilibrium. Could we sustain (lie, lie) somehow? – change the payoffs in the matrix – play the game repeatedly

Another Example - The Price Game Roger u Low High Chris Low High 20, 20 60, 0 0, 60 100, 100 Roger’s best response function: – If Chris goes low, then Roger should go low – If Chris goes high, then Roger should high u Chris’s best response function: – If Roger goes low, then Chris should go low – If Roger goes high, then Chris should go high u u u Two Nash Equilibria: (low, low) and (high, high) Respective Nash equilibrium payoffs: (20, 20) and (100, 100) Which equilibrium will prevail? Good question.

The Price Game (Nash & Maximin Equilibrium) Low Roger High u u u u Chris Low High 20, 20 60, 0 0, 60 100, 100 u So, (Low, Low) is not only a Nash equilibirum it is a maximin equilibrium as well! If Roger goes LOW, the worst that can happen is he gets 20. If Roger goes HIGH, the worst that can happen is he gets 0. The best of the worst case scenarios is 20. So LOW is a maximin strategy for Roger. If Chris goes LOW, the worst that can happen is he gets 20. If Chris goes HIGH, the worst that can happen is he gets 0. The best of the worst case scenarios is 20. So LOW is a maximin strategy for Chris.

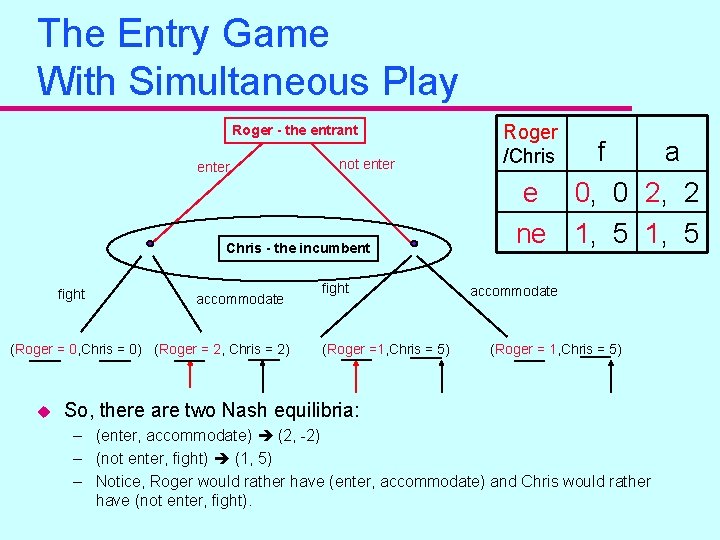
The Entry Game With Simultaneous Play Roger - the entrant enter not enter Chris - the incumbent fight accommodate (Roger = 0, Chris = 0) (Roger = 2, Chris = 2) u fight (Roger =1, Chris = 5) Roger /Chris f a e 0, 0 2, 2 ne 1, 5 accommodate (Roger = 1, Chris = 5) So, there are two Nash equilibria: – (enter, accommodate) (2, -2) – (not enter, fight) (1, 5) – Notice, Roger would rather have (enter, accommodate) and Chris would rather have (not enter, fight).

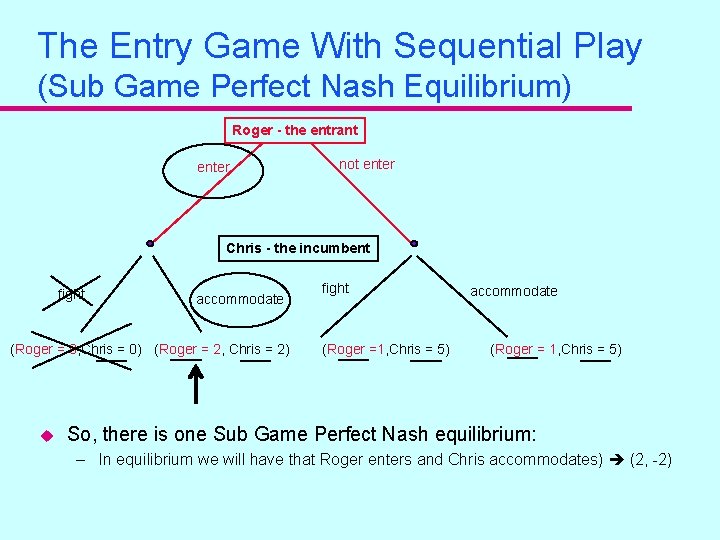
The Entry Game With Sequential Play (Sub Game Perfect Nash Equilibrium) Roger - the entrant enter not enter Chris - the incumbent fight accommodate (Roger = 0, Chris = 0) (Roger = 2, Chris = 2) u fight (Roger =1, Chris = 5) accommodate (Roger = 1, Chris = 5) So, there is one Sub Game Perfect Nash equilibrium: – In equilibrium we will have that Roger enters and Chris accommodates) (2, -2)