G R U P U R I Grupul

G R U P U R I

Grupul rotaţiilor Cn Grupul dihedral Dn Grupul permutărilor Sn Grupul alternativ An Grupul cuaternionilor H 8 Grupul matricilor Pauli Grupurile poliedrelor Relaţii şi generatori Izomorfisme Subgrupuri Diagrame Cayley Ordinul grupului şi elementului

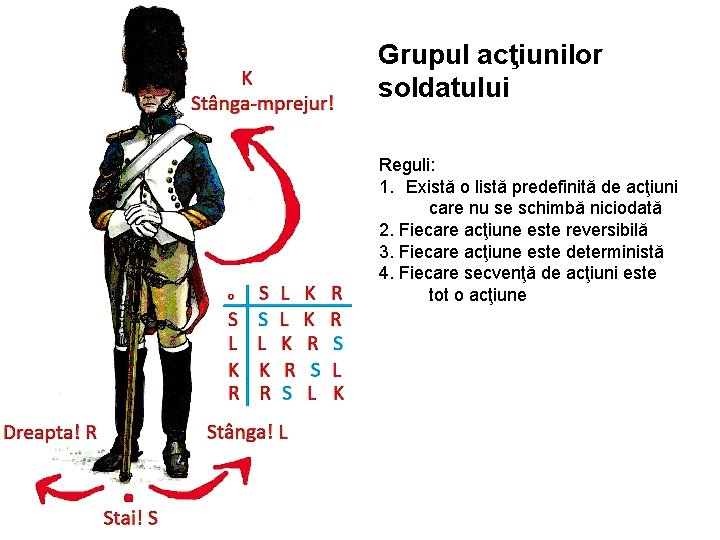
Grupul acţiunilor soldatului Reguli: 1. Există o listă predefinită de acţiuni care nu se schimbă niciodată 2. Fiecare acţiune este reversibilă 3. Fiecare acţiune este deterministă 4. Fiecare secvenţă de acţiuni este tot o acţiune

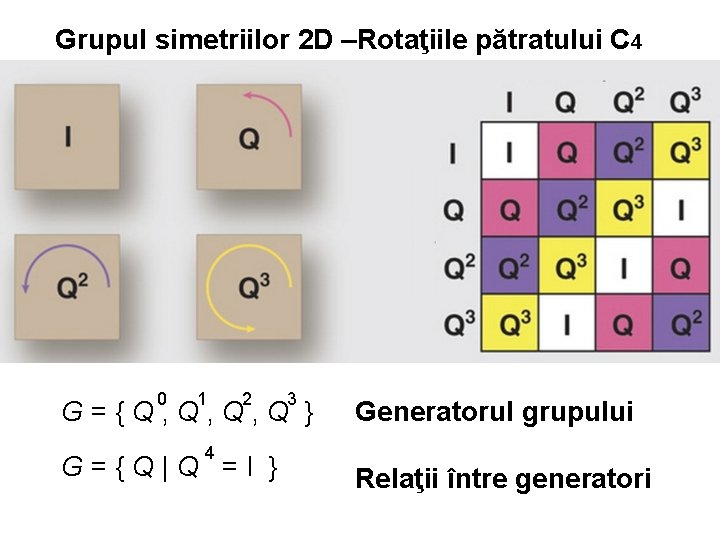
Grupul simetriilor 2 D –Rotaţiile pătratului C 4 0 1 2 3 G = { Q , Q , Q } 4 G = { Q | Q = I } Generatorul grupului Relaţii între generatori

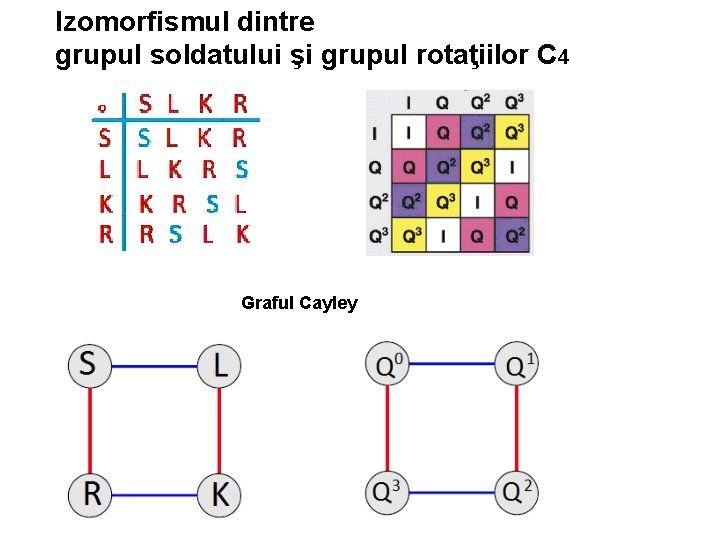
Izomorfismul dintre grupul soldatului şi grupul rotaţiilor C 4 Graful Cayley

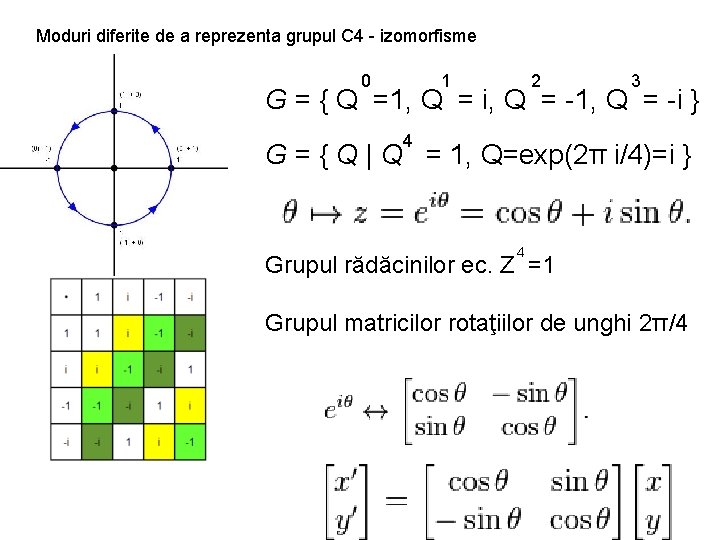
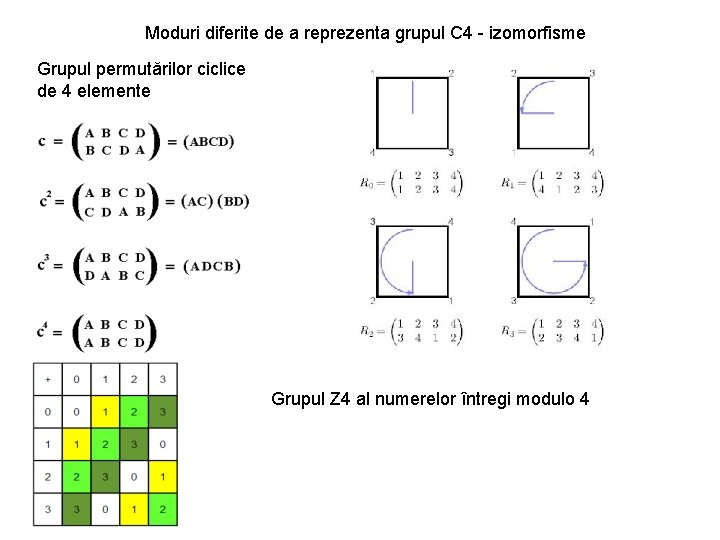
Moduri diferite de a reprezenta grupul C 4 - izomorfisme 0 1 2 3 G = { Q =1, Q = i, Q = -1, Q = -i } 4 G = { Q | Q = 1, Q=exp(2π i/4)=i } 4 Grupul rădăcinilor ec. Z =1 Grupul matricilor rotaţiilor de unghi 2π/4

Moduri diferite de a reprezenta grupul C 4 - izomorfisme Grupul permutărilor ciclice de 4 elemente Grupul Z 4 al numerelor întregi modulo 4

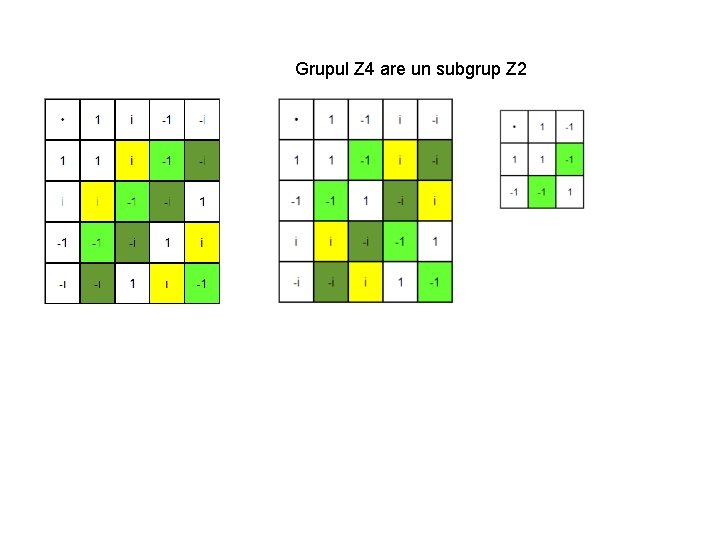
Grupul Z 4 are un subgrup Z 2

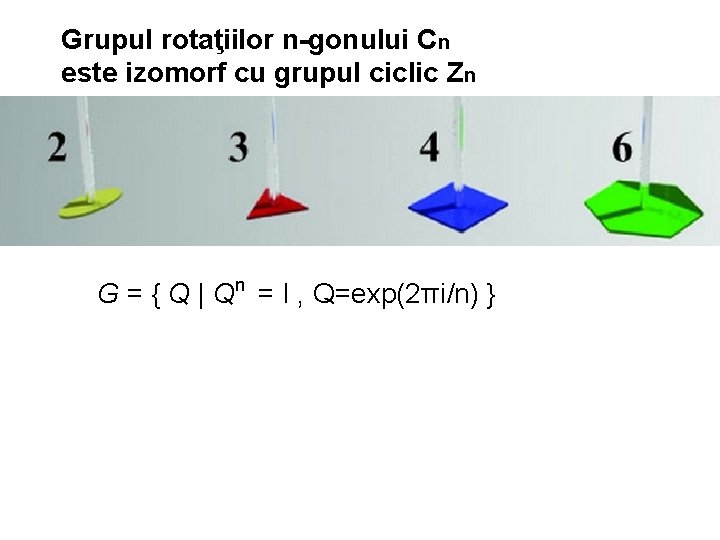
Grupul rotaţiilor n-gonului Cn este izomorf cu grupul ciclic Zn n G = { Q | Q = I , Q=exp(2πi/n) }

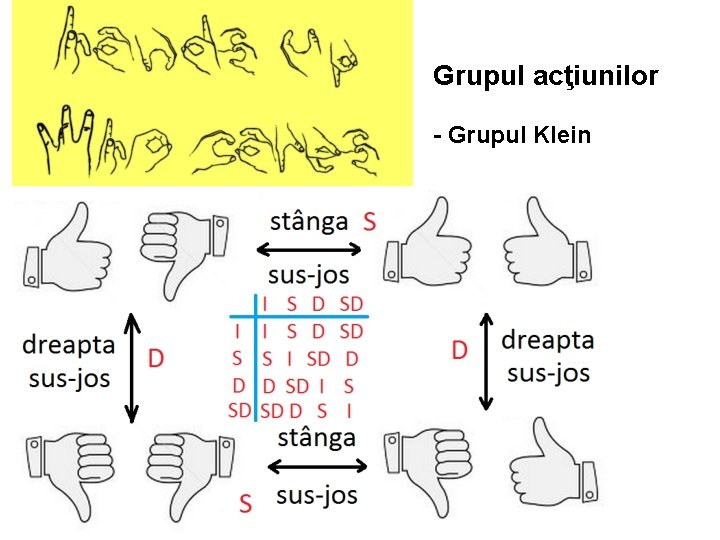
Grupul acţiunilor - Grupul Klein

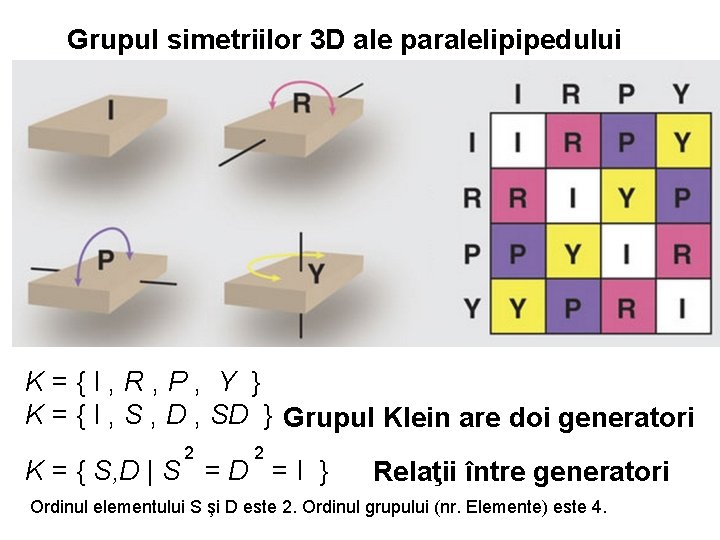
Grupul simetriilor 3 D ale paralelipipedului K = { I , R , P , Y } K = { I , S , D , SD } Grupul Klein are doi generatori 2 2 K = { S, D | S = D = I } Relaţii între generatori Ordinul elementului S şi D este 2. Ordinul grupului (nr. Elemente) este 4.

K = { I , R , P , Y } K = { I , S , D , SD } Grupul Klein are doi generatori 2 2 K = { S, D | S = D = I } Relaţii între generatori Teorema Lagrange - dacă G este un grup finit, atunci ordinul (numărul de elemente) al oricărui subgrup H divide ordinul lui G Ordinul grupului Klein este 4. Ordinul elementului S şi D este 2. Elementele S şi D formează subgrupuri ciclice C 2 de ordin 2 care-l divid pe 4. Putem interpreta reflexiile S şi D ca fiind transpoziţii de 4 elemente. (Transpoziţiile sunt permutări de numai 2 elemente din cele n disponibile.

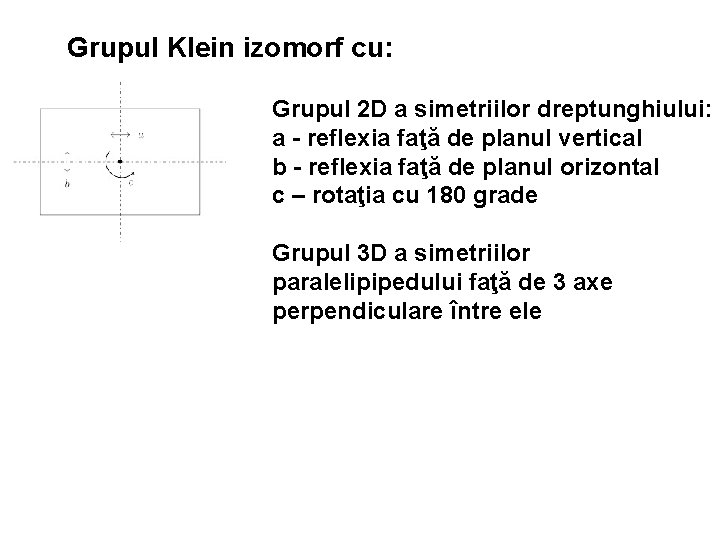
Grupul Klein izomorf cu: Grupul 2 D a simetriilor dreptunghiului: a - reflexia faţă de planul vertical b - reflexia faţă de planul orizontal c – rotaţia cu 180 grade Grupul 3 D a simetriilor paralelipipedului faţă de 3 axe perpendiculare între ele

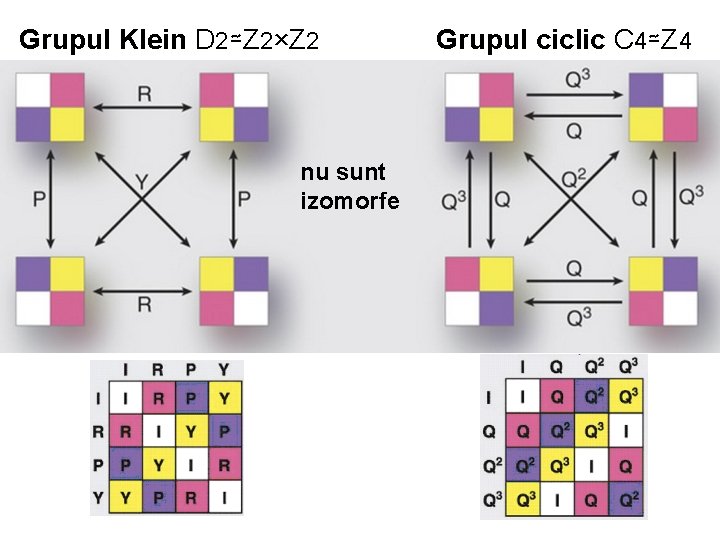
Grupul Klein D 2≃Z 2×Z 2 nu sunt izomorfe Grupul ciclic C 4≃Z 4

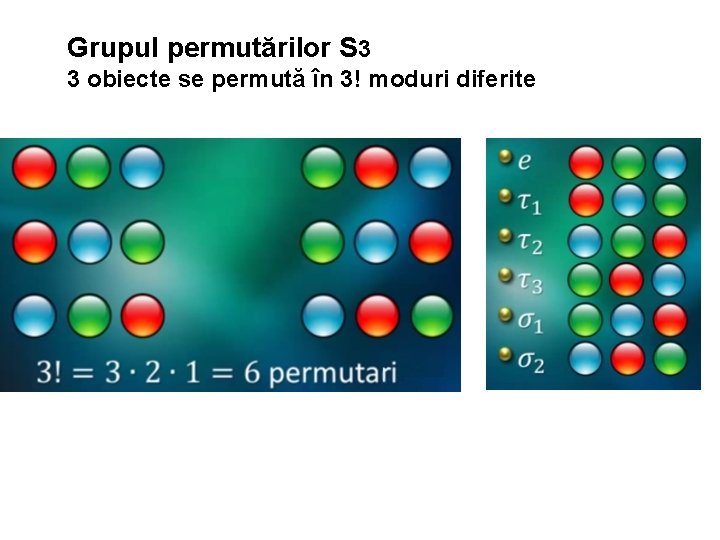
Grupul permutărilor Sn n obiecte se permută în n! moduri diferite 3 obiecte se permută în 3! moduri diferite Relaţii între generatori care sunt transpoziţii Teorema Cayley Orice grup finit G este un subgrup al grupului permutărilor Sn

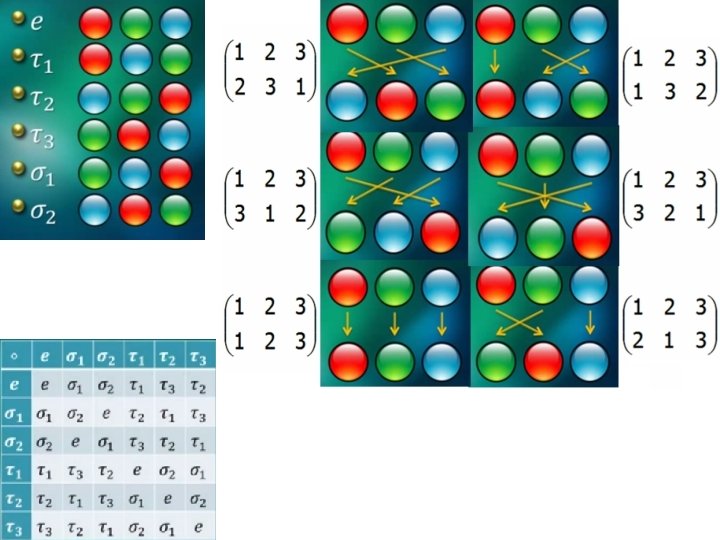
Grupul permutărilor S 3 3 obiecte se permută în 3! moduri diferite

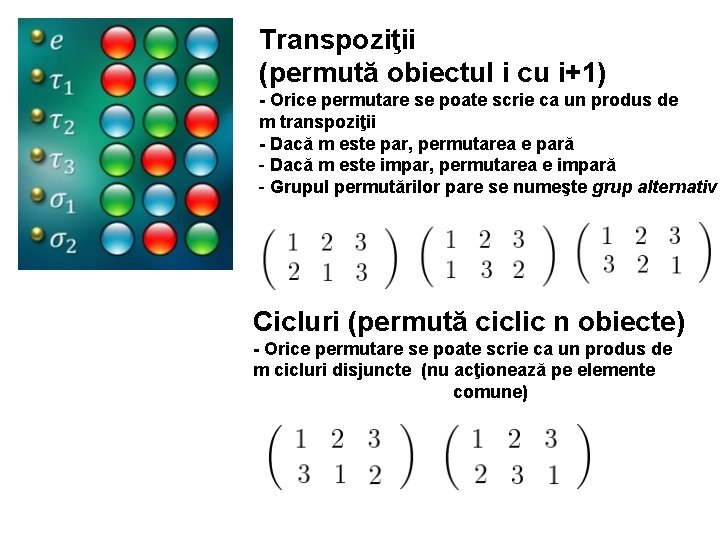
Transpoziţii (permută obiectul i cu i+1) - Orice permutare se poate scrie ca un produs de m transpoziţii - Dacă m este par, permutarea e pară - Dacă m este impar, permutarea e impară - Grupul permutărilor pare se numeşte grup alternativ Cicluri (permută ciclic n obiecte) - Orice permutare se poate scrie ca un produs de m cicluri disjuncte (nu acţionează pe elemente comune)

Relaţiile dintre generatorii grupului S 3

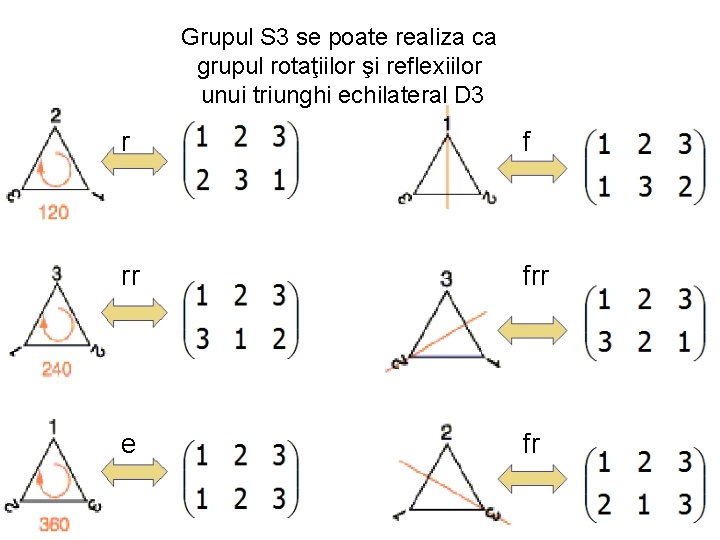
Grupul S 3 se poate realiza ca grupul rotaţiilor şi reflexiilor unui triunghi echilateral D 3 r f rr frr e fr

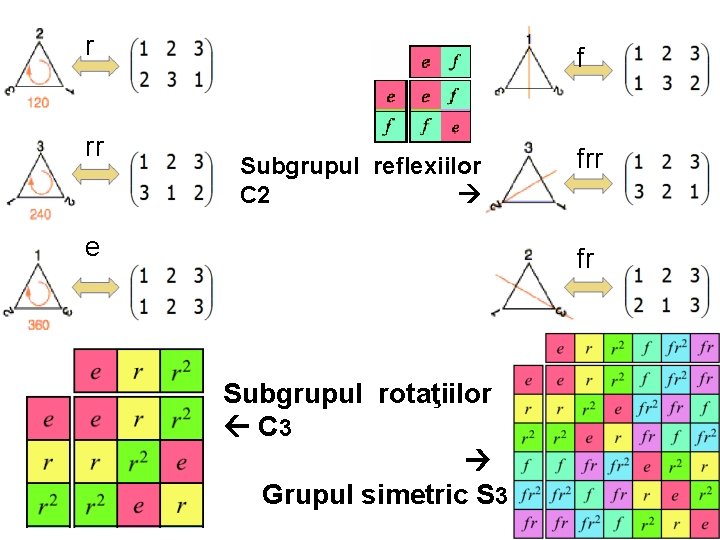
r rr f Subgrupul reflexiilor C 2 e frr fr Subgrupul rotaţiilor C 3 Grupul simetric S 3

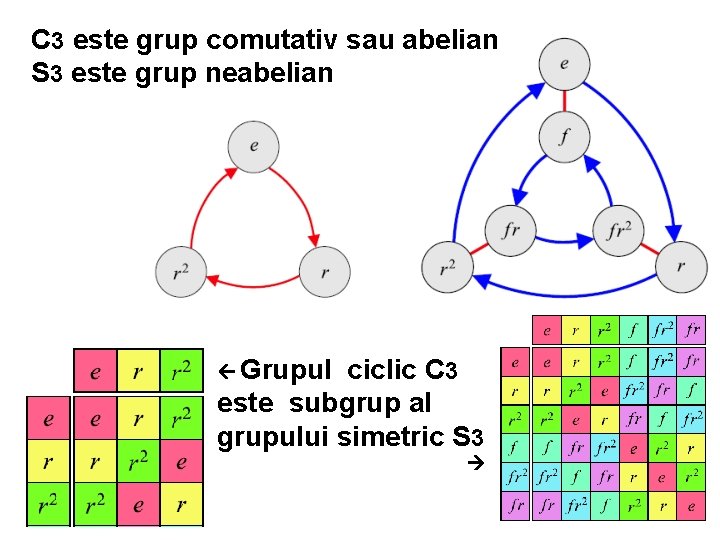
C 3 este grup comutativ sau abelian S 3 este grup neabelian Grupul ciclic C 3 este subgrup al grupului simetric S 3

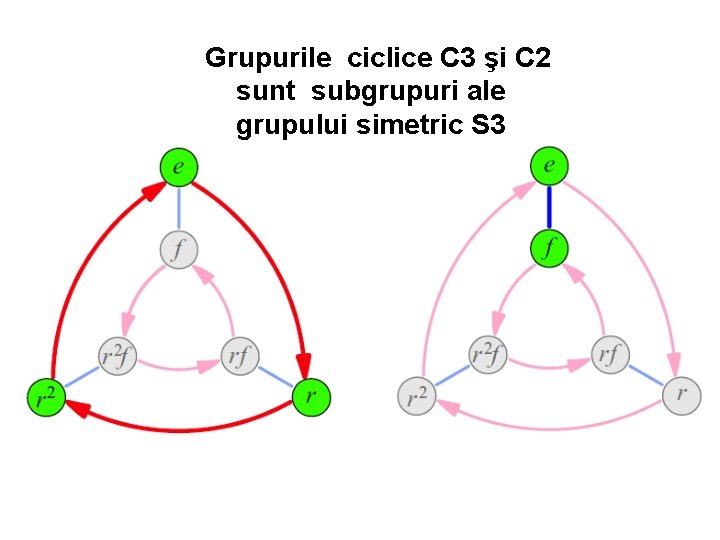
Grupurile ciclice C 3 şi C 2 sunt subgrupuri ale grupului simetric S 3

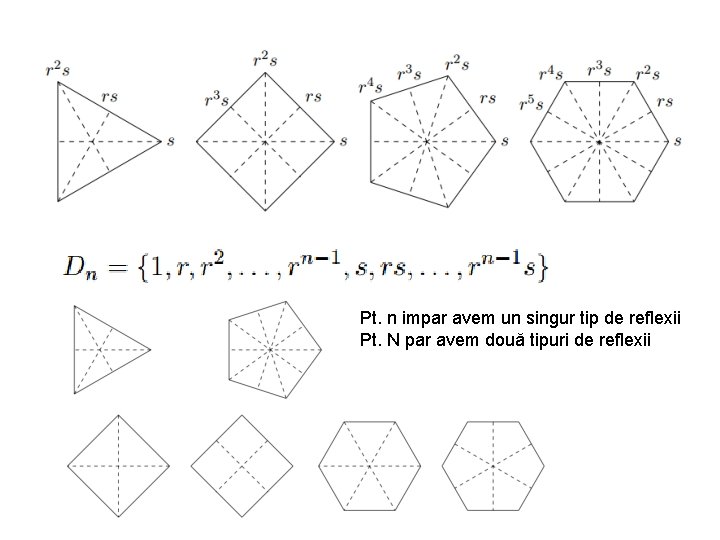
Grupul rotaţiilor Rk şi reflexiilor Sk unui poligon regulat cu n laturi este grupul diedral Dn. Relaţiile între generatori sunt: D 2 grupul Klein este izomorf cu Z 2 x. Z 2 D 3 este izomorf cu S 3

Pt. n impar avem un singur tip de reflexii Pt. N par avem două tipuri de reflexii

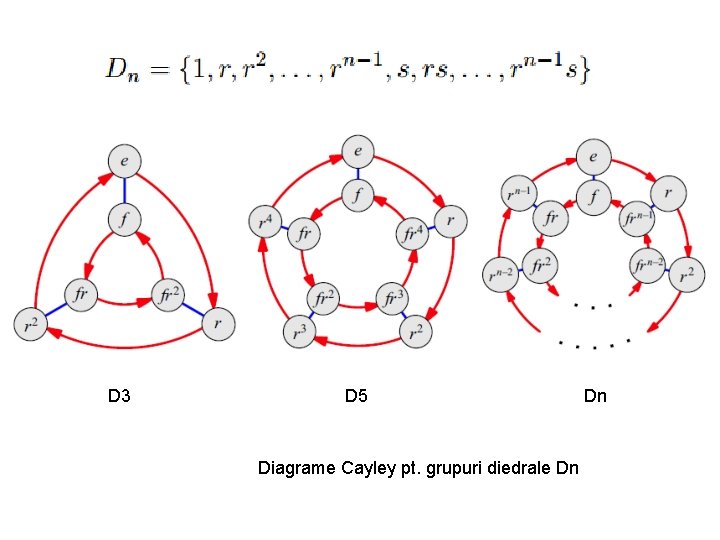
D 3 D 5 Dn Diagrame Cayley pt. grupuri diedrale Dn

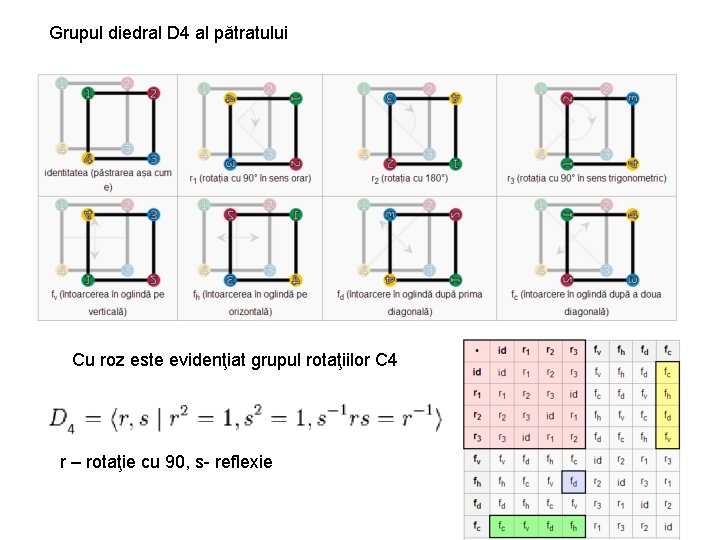
Grupul diedral D 4 al pătratului Cu roz este evidenţiat grupul rotaţiilor C 4 r – rotaţie cu 90, s- reflexie

Grupul diedral D 4 al pătratului este izomorf cu grupul matricilor: Găsiţi care sunt generatorii acestui grup, arătaţi că satisfac aceleaşi relaţii ca şi D 4. Scrieţi matricile anterioare în funcţie de generatori. Arătaţi că a şi b satisfac relaţiile grupului diedral D 4 Graful Cayley pt. D 4

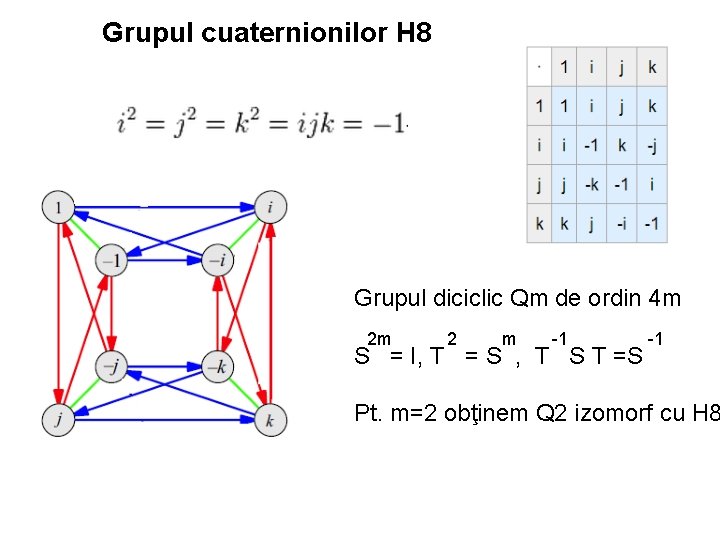
Grupul cuaternionilor H 8 Grupul diciclic Qm de ordin 4 m 2 m 2 m -1 S = I, T = S , T S T =S Pt. m=2 obţinem Q 2 izomorf cu H 8

Grupul matricilor Pauli Există un izomorfism între grupul cuaternionilor şi grupul matricilor Pauli

Toate tipurile de grupuri finite de ordin ≤ 12: 1) (de ordin 1) grupul cu un element 2) (de ordin 2) grupul ciclic C 2 3) (de ordin 3) grupul ciclic C 3 4) (de ordin 4) grupul ciclic C 4 şi grupul lui Klein C 2 × C 2 5) (de ordin 5) grupul ciclic C 5 6) (de ordin 6) grupul ciclic C 6 şi grupul simetric S 3≈D 3≈A 3 7) (de ordin 7) grupul ciclic C 7 8) (de ordin 8) Grupul ciclic C 8, grupul C 4 × C 2, grupul C 2 × C 2 ≈D 2 x. C 2, grupul diedral D 4 şi grupul cuaternionilor H 8 ≈Q 2 9) (de ordin 9) grupul ciclic C 9 şi grupul C 3 × C 3 10) (de ordin 10) grupul ciclic C 10 şi grupul diedral D 5 11) (de ordin 11) grupul ciclic C 11 12) (de ordin 12) grupul ciclic C 12, grupul C 6 x. C 2≈C 3 x. D 2, grupul diedral D 6, grupul diciclic Q 3, grupul alternativ A 4. Singurele grupuri finite de simetrie (de rotaţie) posibile în trei dimensiuni sunt: Cn, Dn, A 4, S 4, A 5 Sau dacă se consideră şi inversiile (x -x) atunci: Cn x C 2, Dn x C 2, A 4 x C 2, S 4 x C 2, A 5 x C 2