FUNCIONES Profesor Javier Chaca Alfaro TEORA DE FUNCIONES

FUNCIONES Profesor: Javier Chaca Alfaro.

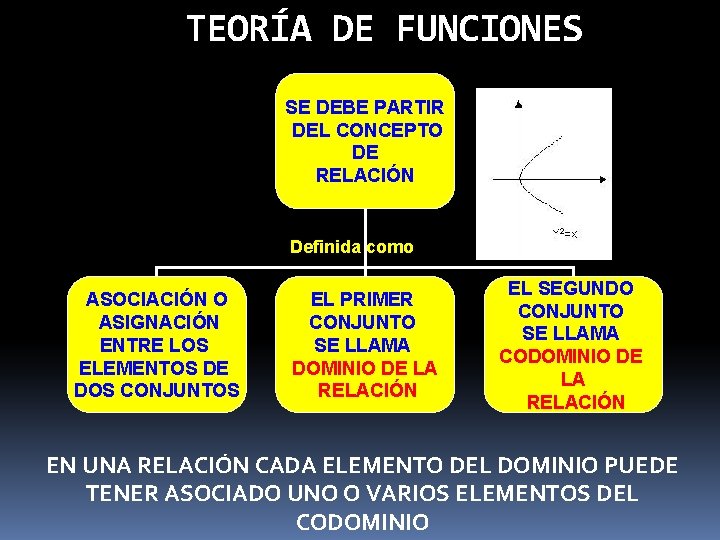
TEORÍA DE FUNCIONES SE DEBE PARTIR DEL CONCEPTO DE RELACIÓN Definida como ASOCIACIÓN O ASIGNACIÓN ENTRE LOS ELEMENTOS DE DOS CONJUNTOS EL PRIMER CONJUNTO SE LLAMA DOMINIO DE LA RELACIÓN EL SEGUNDO CONJUNTO SE LLAMA CODOMINIO DE LA RELACIÓN EN UNA RELACIÓN CADA ELEMENTO DEL DOMINIO PUEDE TENER ASOCIADO UNO O VARIOS ELEMENTOS DEL CODOMINIO

Concepto de función La palabra “función” es utilizada en nuestro lenguaje común para expresar que algunos hechos dependen de otros. Así, la idea matemática de función no es un concepto nuevo, sino una formalización de nuestra idea intuitiva

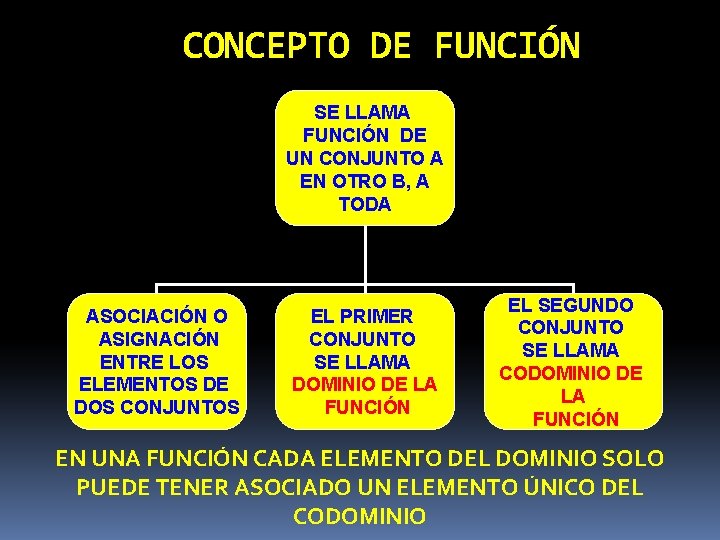
CONCEPTO DE FUNCIÓN SE LLAMA FUNCIÓN DE UN CONJUNTO A EN OTRO B, A TODA ASOCIACIÓN O ASIGNACIÓN ENTRE LOS ELEMENTOS DE DOS CONJUNTOS EL PRIMER CONJUNTO SE LLAMA DOMINIO DE LA FUNCIÓN EL SEGUNDO CONJUNTO SE LLAMA CODOMINIO DE LA FUNCIÓN EN UNA FUNCIÓN CADA ELEMENTO DEL DOMINIO SOLO PUEDE TENER ASOCIADO UN ELEMENTO ÚNICO DEL CODOMINIO

Términos Básicos de una Función Dominio: Es el primer conjunto que intervienen en la función (conjunto A o X) también se le llama conjunto de partida. Se denota por DOM(f) Codominio: Es el segundo conjunto que intervienen en la función (conjunto B o Y) también se le llama conjunto de Llegada. Se denota por COD(f). Rango: los elementos de B que están asociados con los elementos de A forman otro conjunto denominado Rango o Recorrido de la Función. Se denota por Ran(f) Imagen: si x es un elemento del Dominio, la notación f (x) se utiliza para designar el elemento en el recorrido que corresponde a X en la función f, y se denomina Imagen de X. NOTA: TODA FUNCIÓN ES UNA RELACIÓN, PERO NO TODA RELACIÓN ES UNA FUNCIÓN.

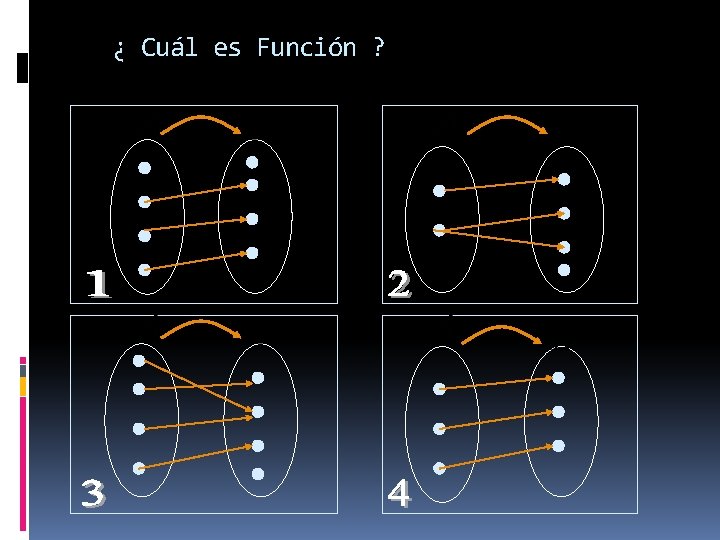
¿ Cuál es Función ?

Dominio y Recorrido en el plano cartesiano

FORMAS DE REPRESENTAR FUNCIONES POR DIAGRAMAS CARTESIANOS POR FÓRMULAS O ECUACIONES POR DIAGRAMAS SAGITALES POR TABLAS DE VALORES POR EXTENSIÓN POR COMPRENSIÒN

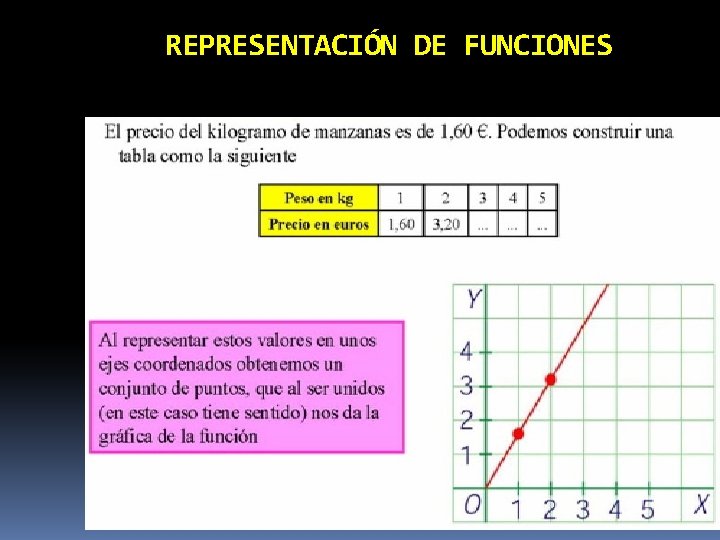
REPRESENTACIÓN DE FUNCIONES

¿Cual es el Dominio y Recorrido de la siguiente función? Dominio Buscar condiciones para la variable Recorrido Buscar condiciones para la variable

Tabla de Evaluación Y su grafica es Menú

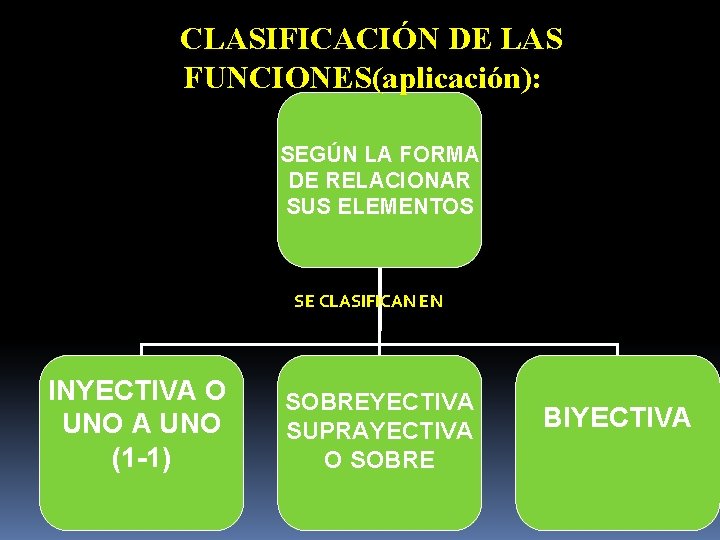
CLASIFICACIÓN DE LAS FUNCIONES(aplicación): SEGÚN LA FORMA DE RELACIONAR SUS ELEMENTOS SE CLASIFICAN EN INYECTIVA O UNO A UNO (1 -1) SOBREYECTIVA SUPRAYECTIVA O SOBRE BIYECTIVA

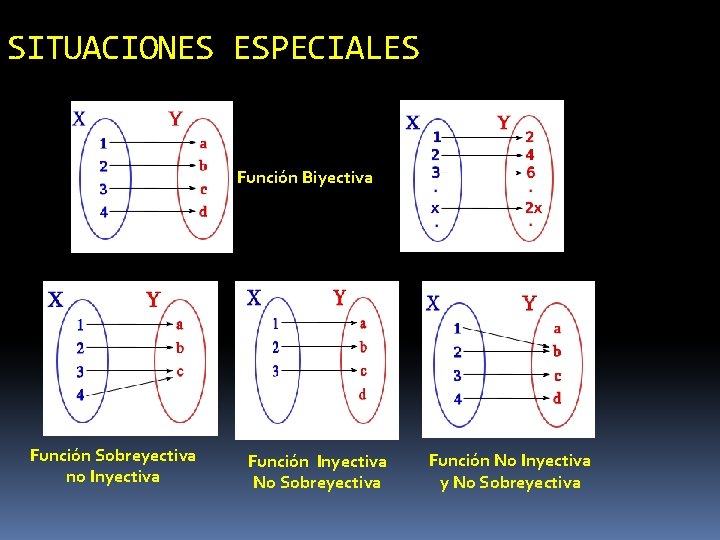
SITUACIONES ESPECIALES Función Biyectiva Función Sobreyectiva no Inyectiva Función Inyectiva No Sobreyectiva Función No Inyectiva y No Sobreyectiva

Ejemplo: Determine si la función f(x) = 3 x + 8 es una función inyectiva. Solución: 3 x 1 + 8 = 3 x 2 + 8 3 x 1 = 3 x 2 x 1 = x 2 Es función inyectiva.

OPERACIONES CON FUNCIONES Suma y diferencia Dadas dos funciones f y g se define la función suma f +g por: (f +g)(x)=f(x)+g(x) Ejemplo 1: Sea f(x)= x+3 y g(x) = x 2 + 2 x – 4. (f +g)(x)=f(x)+g(x) = x+3 + x 2 + 2 x – 4 = x 2 + 3 x – 1. Ejemplo 2: Sea f(x)= 4 x+1 y g(x) = x 2 + 3 x – 1 Determinar: (f +g)(x)=f(x)+g(x)

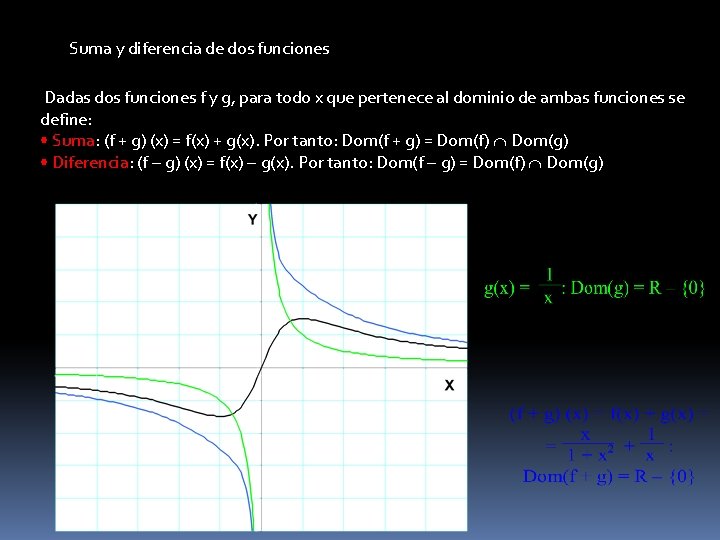
Suma y diferencia de dos funciones Dadas dos funciones f y g, para todo x que pertenece al dominio de ambas funciones se define: • Suma: (f + g) (x) = f(x) + g(x). Por tanto: Dom(f + g) = Dom(f) Dom(g) • Diferencia: (f - g) (x) = f(x) - g(x). Por tanto: Dom(f - g) = Dom(f) Dom(g)

PRODUCTO Dadas dos funciones f y g se define la función producto f. g así (f. g)(x)= f(x). g(x) Ejemplo 1: Sea f(x) = x+3 y g(x)= x 2 + 2 x – 4. (f. g)(x)=f(x). g(x) = (x+3). ( x 2 + 2 x – 4) = x 3 + 2 x 2– 4 x + 3 x 2+6 x -12 = x 3 + 5 x 2 + 2 x – 12 Ejemplo 2: Sea f(x)= x+5 y g(x)= x 2 + 3 x – 2

COCIENTE Dadas dos funciones f y g se define la función cociente f/g por: (f/g)(x) = f(x)/g(x), siempre que g(x) sea distinto de 0. Ejemplo: Sea f(x)= x+3 y g(x)= x 2 + 2 x – 4

Practica calificada 1. Hallar “a + b”, si el conjunto de pares ordenados representa una función. F = {(1; 3), (2; a - b), (3; 3 a + b), (3; 14), (2; 2)} a) 1 b) 2 c) 3 d) 4 e) 6 2. Si se sabe que f( - 1) = 4 y f(3) = - 2, donde “f” es una función lineal. Halla la ecuación que define f(x). 3. Halla el dominio, rango y la grafica de las siguientes funciones reales: a. f(x) = 3 x + 5 b. f(x) = 4 x – 1 x ϵ < -2; 5]

Hallar el dominio, rango y la gráfica de la función. 1. 2. 3. 4. g(x)= x 2 + 2 x – 4 f(x) = x 2 – 4 x + 3 f(x) = 2 x 2 – 12 x + 5; x ϵ [-1; 4> f(x) = – x 2 – 6 x + 2