Frank Cowell Microeconomics November 2006 Exercise 5 2

Frank Cowell: Microeconomics November 2006 Exercise 5. 2 MICROECONOMICS Principles and Analysis Frank Cowell

Ex 5. 2(1): Question Frank Cowell: Microeconomics n n purpose: construct a simple model of investment in the context of household supply method: combine answer to Ex 5. 1 and a straightforward income-maximisation problem

Ex 5. 2(1): Find optimal investment Frank Cowell: Microeconomics n n n Net income is y = p. R 1 + R 2 + bp[1 – e–z] – z Maximise this where dy — = bpe–z – 1 = 0 dz Solve this to get z = log (bp), which is positive if bp 1. So optimal investment is z*(p, b) = max (log (bp), 0) Note dependence on price p and on investment productivity b

Ex 5. 2(2): Question Frank Cowell: Microeconomics method: n Use the result from part 1 n Work out the modified expression for income n Combine this with answer to Ex 5. 1

Ex 5. 2(2): Find supply of rice Frank Cowell: Microeconomics n Maximised income is y*(p, b) = p. R 1 + R 2 + bp[1 – exp(–z*(p, b))] – z*(p, b) n Using the formula for optimal investment z* we find u u n if bp >1: y*(p, b) = p. R 1 + R 2 + bp[1 – 1/bp] – log (bp)) = p. R 1 + R 2 + bp – 1 – log (bp)) otherwise y*(p, b) = p. R 1 + R Using answer to Ex 5. 1 supply of rice is now y*(p, b) – k S*(p, b) = R 1 – a ————— p u u where a and k are parameters of the utility function and y*(p, b) takes one of the two forms above t depends on whether or not p > 1/b

Ex 5. 2(3): Question Frank Cowell: Microeconomics method: n Use the result from parts 1 and 2 n Differentiate with respect to p and b to get responses

Ex 5. 2(3): Investment response Frank Cowell: Microeconomics n n Optimal investment is z*(p, b) = max (log (bp), 0) If p 1/b then, differentiating: z*(p, b) 1 ———— = — > 0 p b z*(p, b) 1 ———— = — > 0 b p n Otherwise z* is constant at 0
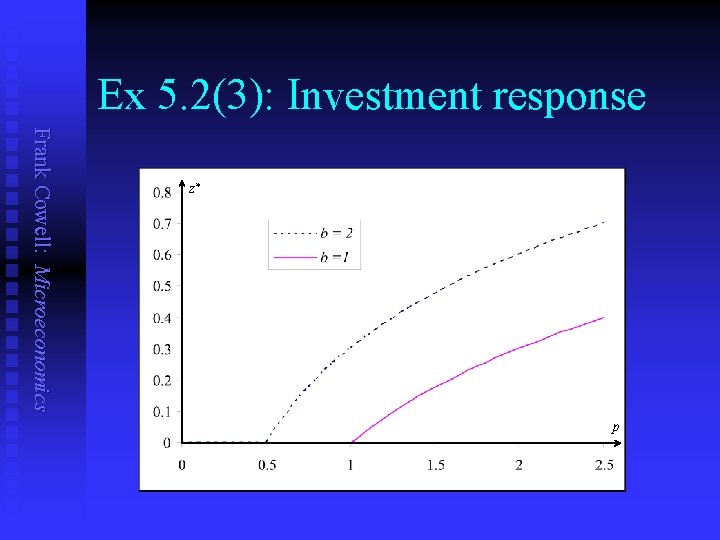
Ex 5. 2(3): Investment response Frank Cowell: Microeconomics z* p

Ex 5. 2(3): Supply response (i) Frank Cowell: Microeconomics n n n If p 1/b maximised income is p. R 1 + R 2 + bp – 1 – log (bp) So supply of rice is R 2 – k – 1 – log (bp) * S (p, b) = [1–a ]R 1+ ab – a ————— p • If R 2 > k positive for small p Differentiating: • maybe negative for large p S*(p, b) R 2 – k – log (bp) ———— = a ——————— p p 2 S*(p, b) 1 – bp ———— = a ——— b bp • non-positive

Ex 5. 2(3): Supply response (ii) Frank Cowell: Microeconomics n n If p < 1/b maximised income is p. R 1 + R 2 So supply of rice is R 2 – k = R 1 – a ——— p • If R 2 > k positive for all p < 1/b Differentiating: S*(p, b) n S*(p, b) R 2 – k ———— = a —— p p 2 S*(p, b) ———— = 0 b

Ex 5. 2: Points to remember Frank Cowell: Microeconomics n n n Make good use of answers to previous parts in each stage When analysing optimal investment take care about the corner solution Use the two cases (corner, interior solution) in modelling the agent’s response to price and productivity changes
- Slides: 11





















