Forward pricing Assets with no cash flows Assets

Forward pricing Assets with no cash flows Assets with known discrete cash flows Assets with continuous cash flows (index) Finance 70420 Spring 2004 Associate Professor Steven C. Mann The Neeley School of Business at TCU

Forward price of a stock S(0) = $25. Stock pays no dividends is(6 month) = 7. 12% ( T = 1/2 ) if you borrow $25 today you repay $25[1+ 0. 0712(1/2)] = $25. 89 f = six month forward price of stock Consider strategy: borrow $25 buy stock sell 6 -month forward total now 25. 00 - 25. 00 0 0 T=6 months later -$25. 89 S(T) - [ S(T) - f ] f - 25. 89 = f - S(0)[ 1 + is T] Arbitrage-free forward pricing: f (0, T) = S(0)(1 + is. T) = $25. 89

Cash and Carry forward pricing Forward contract with delivery date T; spot asset with no cash flows “Cash and carry” strategy: buy asset at cost S(0) borrow asset cost sell forward at f(0, T) now - S(0) + S(0) 0 at date T S(T) -S(0)(1+is. T) -[ S(T) -f(0, T)] Total 0 f(0, T) - S(0)(1+is. T) f(0, T) = S(0)( 1 + is. T) Forward price is “future value” of spot price f(0, T) [ 1/(1+is. T)] = S(0) = f(0, T)B(0, T) S(t) = f(t, T) B(t, T) Spot price is “present value” of the forward price

Forward valuation (post-initiation and “off-market”) Value = V[forward price, time] at initiation, value is zero: V[ f(0, T), 0 ] 0. At maturity: V[ f(0, T), T ] = S(T) - f(0, T) at some time t (post initiation): V[ f(0, T), t ] = ? 1) Valuation by offset: At time t: value at T: total value at T: value at t: long f(0, T). Sell f(t, T) S(T) - f(0, T) - [ S(T) - f(t, T) ] f(t, T) - f(0, T) B(t, T)[ f(t, T) - f(0, T) ] 2) Valuation by algebra: V[f(0, T), t] = PV( V[f(0, T), T]) = PV[ S(T) - f(0, T)] note S(t) = PV[S(T)]; and so S(t) = f(t, T)B(t, T) (prior page) V(f(0, T), t] = f(t, T)B(t, T) - f(0, T)B(t, T) =B(t, T) [ f(t, T) - f(0, T)] = PV(price difference)

Example: forward pricing and valuation Non-dividend paying asset; S(0) = $65 contract maturity is 90 days simple interest rate is 4. 50% ; daycount is actual/365. a) find forward price f(0, 90/365) = S(0)(1+is(90/365)) = $65(1 + 0. 045(90/365) ) = $65. 72 value of contract is zero. b) You are asked to value a 90 -day forward on this asset with delivery price = $60. This is an “off-market’ forward: value is nonzero. Value of long forward with off-market delivery price: value = PV( difference in forward prices) = B(0, T)[ market forward price - contract forward price] = B(0, T) [ 65. 72 - 60. 00] = (1 + 0. 045(90/365)) -1 [$ 5. 72] =(0. 98903)($5. 72) = $5. 66

Example: forward pricing and valuation S(0) = $45. Non-dividend paying asset contract maturity is 100 days simple interest rate is 4. 75% ; daycount is actual/365. a) find current forward price f(0, 100/365) = $45. 00(1+ 0. 0475(100/365)) = $45. 59 b) You are long 100 day forward to buy asset at $50. 25. If you sell a 100 day forward at current price, what is payoff at T? At maturity: long: short net: S(T) - $50. 25 -[ S(T) - $45. 59] $45. 59 - $50. 25 = - $4. 66. c) what is the present value of your net position? PV = B(t, T)[ f(t, T) - f(0, T)] = [1/(1+0. 0475(100/365)](-4. 66) = (0. 9872)(-4. 66) = -$4. 60

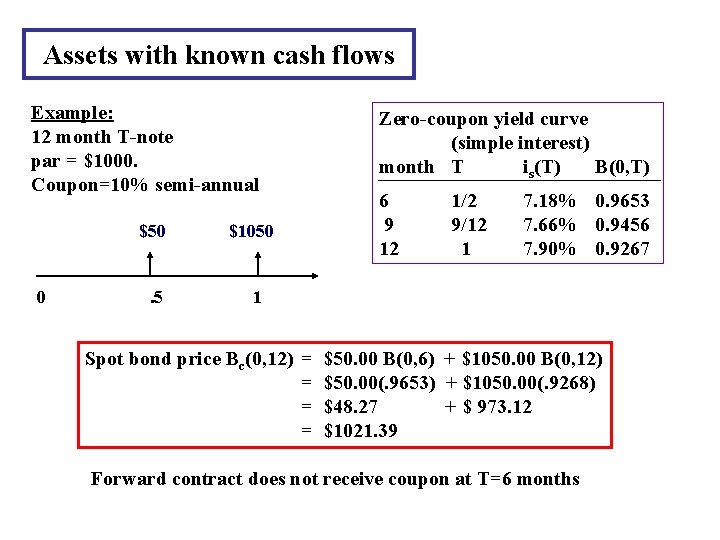
Assets with known cash flows Example: 12 month T-note par = $1000. Coupon=10% semi-annual $50 0 . 5 $1050 Zero-coupon yield curve (simple interest) month T is(T) B(0, T) 6 9 12 1/2 9/12 1 7. 18% 0. 9653 7. 66% 0. 9456 7. 90% 0. 9267 1 Spot bond price Bc(0, 12) = = $50. 00 B(0, 6) + $1050. 00 B(0, 12) $50. 00(. 9653) + $1050. 00(. 9268) $48. 27 + $ 973. 12 $1021. 39 Forward contract does not receive coupon at T=6 months

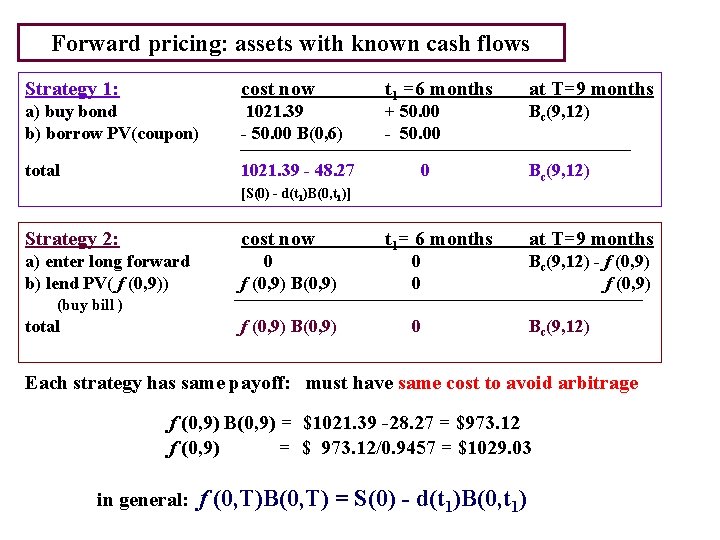
Forward pricing: assets with known cash flows Strategy 1: cost now a) buy bond b) borrow PV(coupon) 1021. 39 - 50. 00 B(0, 6) total 1021. 39 - 48. 27 t 1 =6 months + 50. 00 - 50. 00 0 at T=9 months Bc(9, 12) [S(0) - d(t 1)B(0, t 1)] Strategy 2: cost now a) enter long forward b) lend PV( f (0, 9)) 0 f (0, 9) B(0, 9) t 1= 6 months at T=9 months 0 0 Bc(9, 12) - f (0, 9) 0 Bc(9, 12) (buy bill ) total f (0, 9) B(0, 9) Each strategy has same payoff: must have same cost to avoid arbitrage f (0, 9) B(0, 9) = $1021. 39 -28. 27 = $973. 12 f (0, 9) = $ 973. 12/0. 9457 = $1029. 03 in general: f (0, T)B(0, T) = S(0) - d(t 1)B(0, t 1)

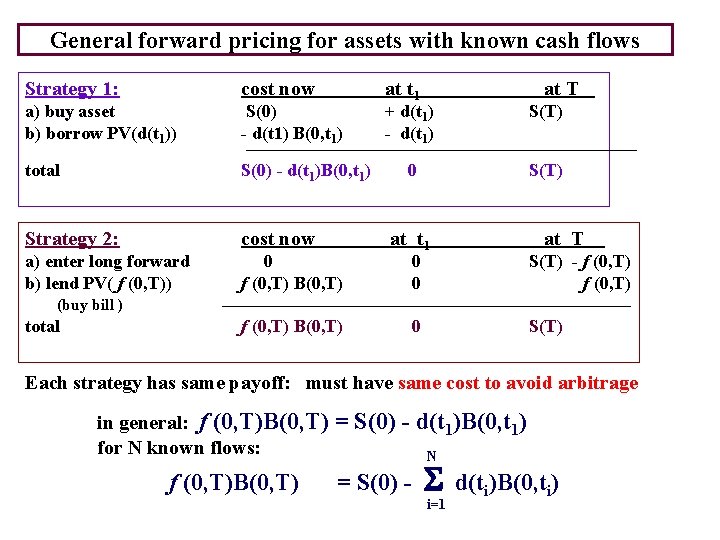
General forward pricing for assets with known cash flows Strategy 1: cost now a) buy asset b) borrow PV(d(t 1)) S(0) - d(t 1) B(0, t 1) total S(0) - d(t 1)B(0, t 1) Strategy 2: cost now a) enter long forward b) lend PV( f (0, T)) 0 f (0, T) B(0, T) at t 1 at T + d(t 1) - d(t 1) S(T) 0 S(T) at t 1 at T 0 0 S(T) - f (0, T) 0 S(T) (buy bill ) total f (0, T) B(0, T) Each strategy has same payoff: must have same cost to avoid arbitrage in general: f (0, T)B(0, T) for N known flows: f (0, T)B(0, T) = S(0) - d(t 1)B(0, t 1) N = S(0) - S i=1 d(ti)B(0, ti)

Example: forward pricing - asset pays dividends S(0) = $63. 375 stock pays dividends: $1. 50 in 1 month $2. 00 in 7 months Bill prices: 1 month: 7 month : 12 month: Find price of one-year forward contract written on stock. Use: f (0, T) B(0, T) = S(0) - PV(dividends) f (0, 12) B(0, 12) f (0, 12) (0. 9512) f (0, 12) = S(0) - d(1)B(0, 1) - d(7)B(0, 7) = $63. 375 - $1. 50(0. 9967) - $2. 00(0. 9741) = $59. 93/(0. 9512) = $63. 01 0. 9967 0. 9741 0. 9512

Assets with continuous payouts (index, currency) for N known flows: f (0, T)B(0, T) N = S(0) - S d(ti)B(0, ti) i=1 = S(0) - PV(cash payout to time T) if asset pays continuous yield then PV(dividends to time T) = S(0)[ 1 - exp(-dy. T)] so that f (0, T)B(0, T) = S(0) - [ S(0) [ 1 - exp(-dy. T)]] f (0, T)B(0, T) = S(0) exp(-dy. T) write B(0, T) as continuous discount factor: B(0, T) = exp(-r. T) then f (0, T) = S(0) exp ( (r-dy)T)

Example: Index forward pricing S&P 500 Index = 495. 00 div yield = 2. 50% continuous (365 day year) a) Given 95 -day discount rate =5. 75% (360 day year), find f (0, 95 days) B(0, 95) = 1 - 0. 0575(95/360) = 0. 984826 exp(-dy. T) = exp(-0. 025(95/365)) = 0. 993514 f (0, 95)B(0, 95) f (0, 95) = S(0)exp(-dy. T) = 495. 00 (0. 993514) / (0. 98426) = 499. 37. b) One day later index is at 493. 94 -day discount is 5. 75%. What is the value of the contract in part (a)? B(0, 94) = 1 - 0. 0575(94/360) = 0. 984986 exp(-dy. T) = exp(-0. 025(94/365)) = 0. 993582 f (0, 94) = 493. 00(0. 993582)/(0. 984986) = 497. 20 value of prior contract = B(0, 94) ( 497. 20 - 499. 37) = 0. 984986 (-2. 17) = -2. 04

Commodity Forwards: Storage cost Storage: Define: G = cost of storing asset for (0, T) (per unit); paid time 0. “Cost of carry” strategy: buy asset at cost S(0), pay storage borrow asset cost and storage cost sell forward at f(0, T) cost now S(0) + G -[S(0) + G] 0 value at date T S(T) -[S(0)+G](1+is. T) -[ S(T) -f(0, T)] Total 0 f(0, T) - [S(0) +G](1+is. T) f (0, T)B(0, T) = S(0) + G Example: 180 -day Gold forward (100 troy oz. ) Spot Gold S(0) = $368 / oz. cost of storage for 180 days = 2. 25 / oz. , paid at time 0. 180 days simple interest rate = 3. 875% annualized (actual/actual). f (0, 180) = (368 + 2. 25)(1 + 0. 03875(180/365)) = 370. 25(1. 01911) = $377. 33 / oz. If storage cost G is defined to be paid at T, then f(0, T)B(0, T) = S(0) + G B(0, T) so f (0, 180) = 368(1+0. 03875(180/365)) + 2. 25 = $377. 28 / oz.

Commodity Forwards: Convenience yield: Define: Y(0, T) = present value (time 0) of benefits provided by holding asset. “Cost of carry” strategy: buy asset at cost S(0), pay storage borrow asset cost and storage cost receive convenience yield sell forward at f(0, T) cost now S(0) + G -[S(0) + G] 0 0 value at date T S(T) -[S(0)+G](1+is. T) Y(0, T)(1+is. T) -[ S(T) -f(0, T)] Total 0 f(0, T) + [S(0) + G -Y(0, T)](1+is. T) f (0, T)B(0, T) = S(0) + G - Y(0, T). Define yn = net convenience yield = Y-G ; where Y and G are continuously compounded rates f (0, T) = S(0) exp[(r-yn)T] Example: 180 -day Gold forward (100 troy oz. ) Spot Gold S(0) = $368 / oz. cost of storage is 0. 25% as continuous annual rate. Gold lease rate (convenience yield) is 1. 50% annual continuously compounded. Yn = 0. 0150 - 0. 0025 = 0. 0125 ( 125 basis points) 180 day continuously compounded rate is 4. 0% f (0, 180) = 368 exp [ ( 0. 04 - (0. 0125))(180/365)] = $368 exp[0. 01356] = 368(1. 01365) = $373. 02

Implied Repo rates Define: i. I as implied repo rate (simple interest). i. I is defined by: f (0, T) = S(0)(1+ i. I T) ; f (0, T) and S(0) are current market prices. Example: asset with no dividend, storage cost, or convenience yield (example: T-bill) Given simple interest rate is, theoretical forward price (model price) is: f (0, T) = S(0)(1+is. T). If i. I > i s i. I < i s market price > model price. market price < model price. If i. I > is : arbitrage strategy : buy asset at cost S(0) borrow asset cost sell forward at f(0, T) cost now value at date T S(0) S(T) -S(0)(1+is. T) 0 -[S(T) -f(0, T)] = Total 0 f(0, T) - S(0)(1+is. T) = S(0)(1+i. IT) - S(0) )(1+is. T) = S(0)(i. I - is)T > 0

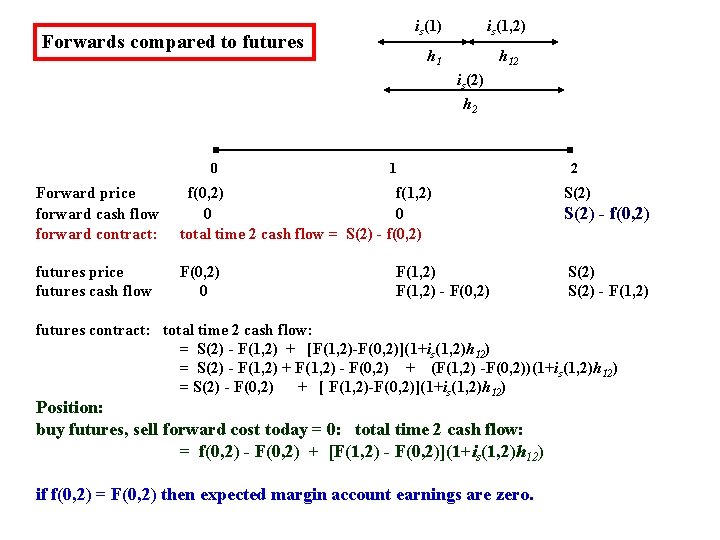
is(1) Forwards compared to futures is(1, 2) h 12 is(2) h 2 0 1 2 Forward price forward cash flow forward contract: f(0, 2) f(1, 2) 0 0 total time 2 cash flow = S(2) - f(0, 2) S(2) futures price futures cash flow F(0, 2) 0 S(2) - F(1, 2) - F(0, 2) S(2) - f(0, 2) futures contract: total time 2 cash flow: = S(2) - F(1, 2) + [F(1, 2)-F(0, 2)](1+is(1, 2)h 12) = S(2) - F(1, 2) + F(1, 2) - F(0, 2) + (F(1, 2) -F(0, 2))(1+is(1, 2)h 12) = S(2) - F(0, 2) + [ F(1, 2)-F(0, 2)](1+is(1, 2)h 12) Position: buy futures, sell forward cost today = 0: total time 2 cash flow: = f(0, 2) - F(0, 2) + [F(1, 2) - F(0, 2)](1+is(1, 2)h 12) if f(0, 2) = F(0, 2) then expected margin account earnings are zero.