Fitting Tree Metrics Hierarchical Clustering and Phylogeny Nir

Fitting Tree Metrics: Hierarchical Clustering and Phylogeny Nir Ailon Moses Charikar Princeton University

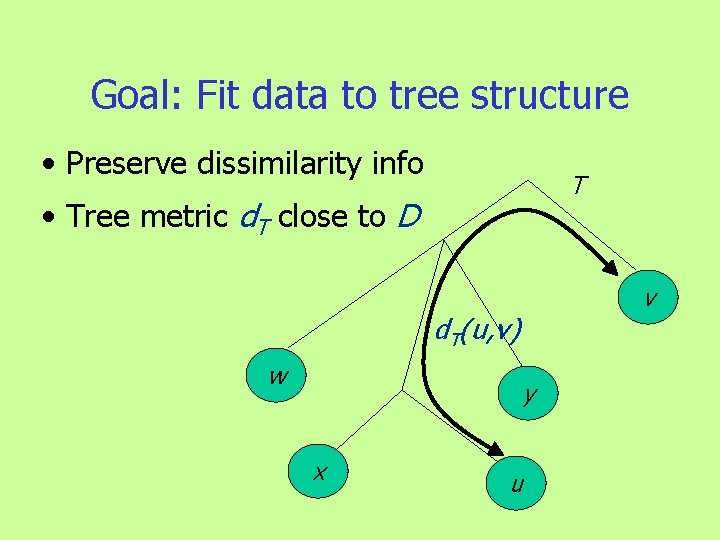
Data with dissimilarity information • Represented by matrix D • Complete information u 10 y D(u, v)=1 7 5 3 x 6 v 2 13 5 8 w (big number = high dissimilarity)

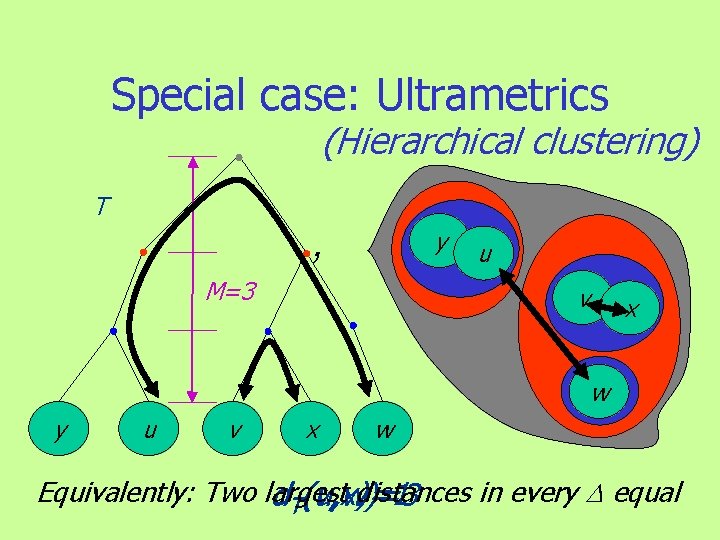
Goal: Fit data to tree structure • Preserve dissimilarity info T • Tree metric d. T close to D v d. T(u, v) w y x u

Objective function Minimize: cost(T) = || D – d. T ||p n -dimensional real vectors 2 ( )

Applications • Evolutionary biology – Molecular phylogeny: Dissimilarity information from DNA • Gene expression analysis • Historical linguistics • . . .

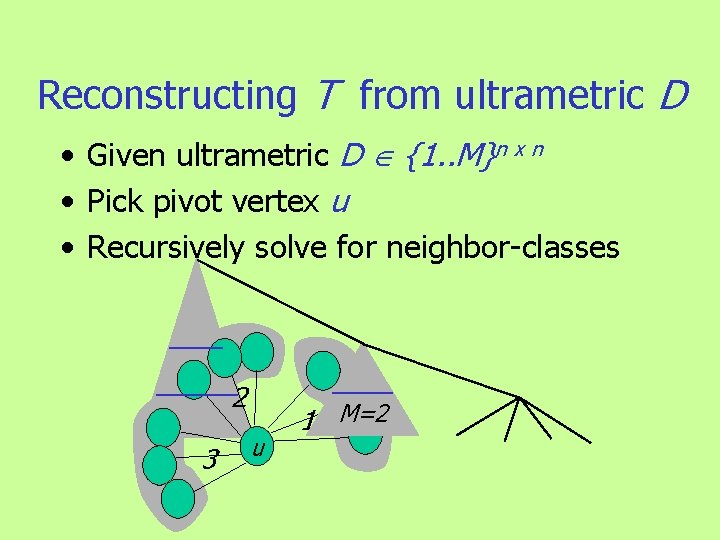
Special case: Ultrametrics (Hierarchical clustering) T , ` M=3 y u v x w Equivalently: Two largest distances in every equal (v, x)=1 d. T(u, w)=3

Previous results • Fitting ultrametrics under ||. || in P [FKW 95] • Fitting trees under ||. || APX-Hard [ABFPT 99] • Fitting ultrametrics under ||. ||1 APX-Hard[W 93] under ||. ||2 NP-Hard • f(n)-approximation algorithm for ultrametrics (3 f(n))-approximation algorithm for trees (under any ||. ||p) [ABFPT 99]

Previous results • O(min{n 1/p, (k logn)1/p})-approx for trees under ||. ||p [HKM 05] • Fitting ultrametrics for M=2 under ||. ||1 : Correlation Clustering [BBC 02, CGW 03, ACN 05. . ] • . . .

Our results • (M+1) – approx for fitting level M ultrametrics under ||. ||1 • O((log n loglog n)1/p) - approx for general weighted trees under ||. ||p

Reconstructing T from ultrametric D • Given ultrametric D {1. . M}n x n • Pick pivot vertex u • Recursively solve for neighbor-classes M=3 3 2 u 1 M=2

Minimizing ||. ||1 for inconsistent D {1. . M}n x n • Same algorithm! • Pick pivot vertex u (uniformly@random) • Freeze distances incident to u • Fix inter-class distances • Fix intra-class distances 2 1 (Total cost contribution: 4) 3 u • Recurse. . . • Lemma: no cancellations • Theorem: M+1 approximation 2 X 3 3 X 1 32 X

Proof idea • violating if: w 1 > 2 ¸ 3 • Optimal solution pays 2 ) 1 1 ) 2 ¸ 1 - 2 • Algorithm charging scheme: v u ) 2)3 1 - 2 w uv chosen as pivot ) charged 1 - 23 + 1 - 2

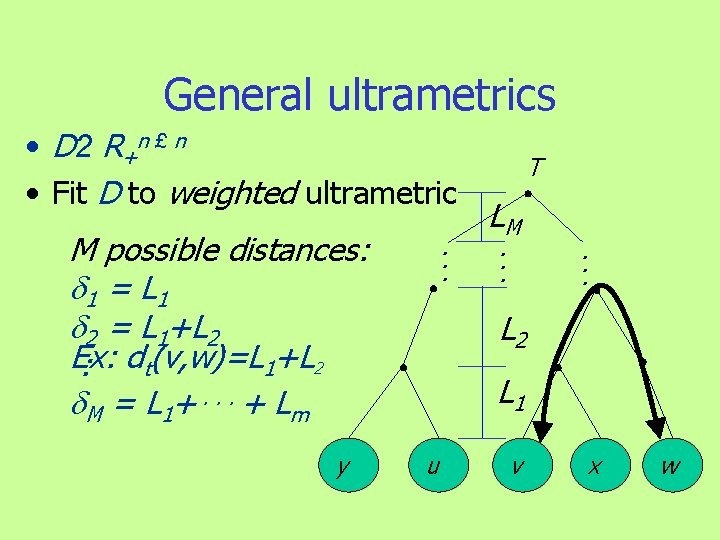
General ultrametrics • D 2 R + n £ n • Fit D to weighted ultrametric M possible distances: 1 = L 1 2 = L 1+L 2 Ex: : dt(v, w)=L 1+L 2 M = L 1 +. . . + L m y . . . T LM. . . L 2 L 1 u v x w

Fitting D to M-level weighted Ultrametric under ||. ||1 Linear [0, 1] relaxationt • Integer program formulation: x uv {0, 1} • xtuv = 1 u, v separated at level t • 0 x. Muv x. M-1 uv . . . x 1 uv=1 T • - inequality at each level x. Muy = 0 L M. . 2. t t t. . uy = xx 1 uv 0 x uw + x wv. . x uy =1 L Cost: 2 • min t=1 M Lt ( xtuv + (1 -xtuv) L) 1 D(u, v) t D(u, v) > t y u v x w

Rounding the LP: An O(logn loglogn)-approximation • • A divisive (top-down) algorithm At each level t=M, M-1, . . . , 1: Solve a multi-cut-like problem Cluster so as to separate u, v ’s s. t. xtuv ¸ 2/3 • Danger: High levels influence low ones!

General ||. ||p cost • Similar analysis gives same bound for ||. ||pp • Therefore: O( logn loglogn )1/p – approximation • By [ABFPT 99], applies also to fitting trees

Future work • • • O( log n) – algorithm? Better? Stronger lower bounds Derandomize (M+1)-approx algorithm Aggregation [ACN 05] Applications Thank You!!!