Federal Department of Home Affairs FDHA Federal Office











- Slides: 24

Federal Department of Home Affairs FDHA Federal Office of Meteorology and Climatology Meteo. Swiss Terrain-following coordinates over steep and high orography Oliver Fuhrer

Outline • Terrain-following coordinates • Two idealized tests • Atmosphere at rest • Constant advection • Possible remedy: SLEVE • How to specify SLEVE parameters?

Overview • Terrain-following coordinates have many advantages. . . - rectangular computational mesh - lower boundary condition - stretching → boundary layer representation • But also many disadvantages. . . - additional terms - horizontal pressure gradient formulation (Janjic, 1989) - metric terms (Klemp et al. , 2003) - truncation error (Schär et al. , 2002)

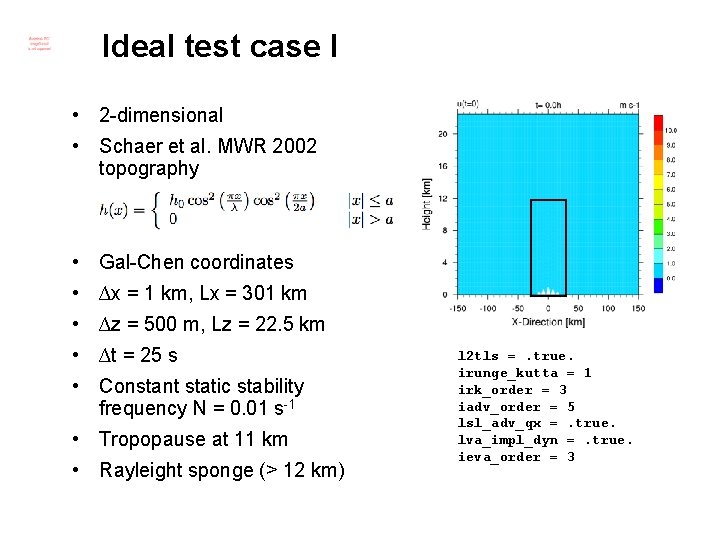
Ideal test case I • 2 -dimensional • Schaer et al. MWR 2002 topography • Gal-Chen coordinates • ∆x = 1 km, Lx = 301 km • ∆z = 500 m, Lz = 22. 5 km • ∆t = 25 s • Constant static stability frequency N = 0. 01 s-1 • Tropopause at 11 km • Rayleight sponge (> 12 km) l 2 tls =. true. irunge_kutta = 1 irk_order = 3 iadv_order = 5 lsl_adv_qx =. true. lva_impl_dyn =. true. ieva_order = 3

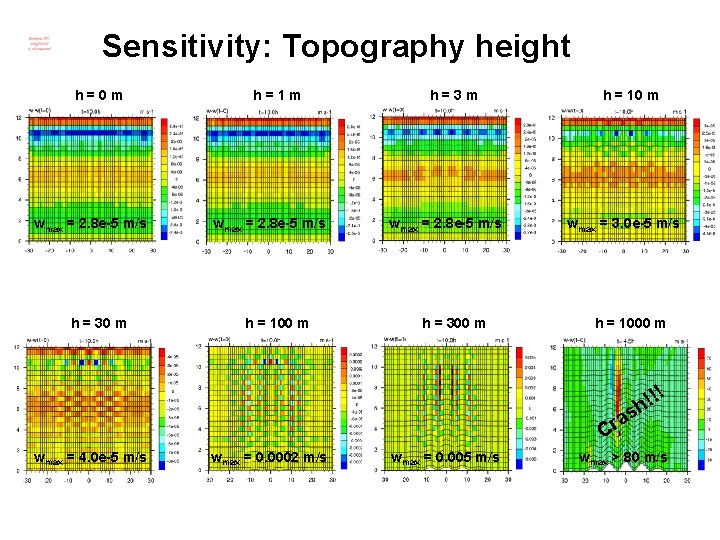
Sensitivity: Topography height h=0 m wmax = 2. 8 e-5 m/s h = 30 m h=1 m wmax = 2. 8 e-5 m/s h = 100 m h=3 m wmax = 2. 8 e-5 m/s h = 300 m h = 10 m wmax = 3. 0 e-5 m/s h = 1000 m !! ! h as r C wmax = 4. 0 e-5 m/s wmax = 0. 0002 m/s wmax = 0. 005 m/s wmax > 80 m/s

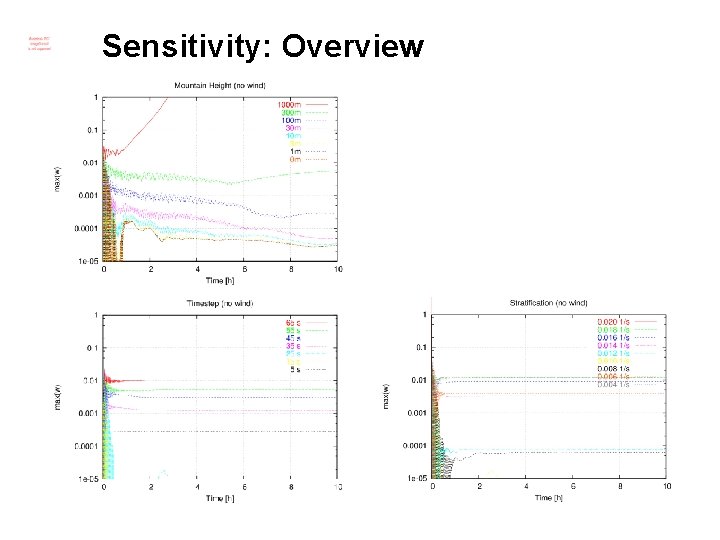
Sensitivity: Overview

Explanation ?

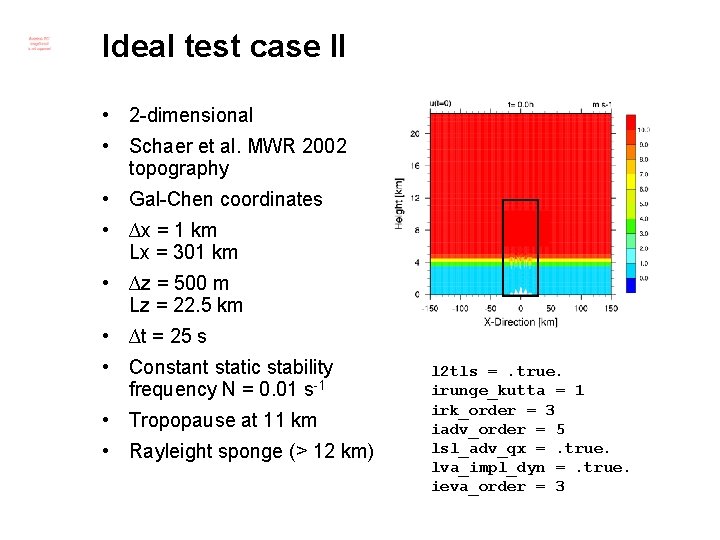
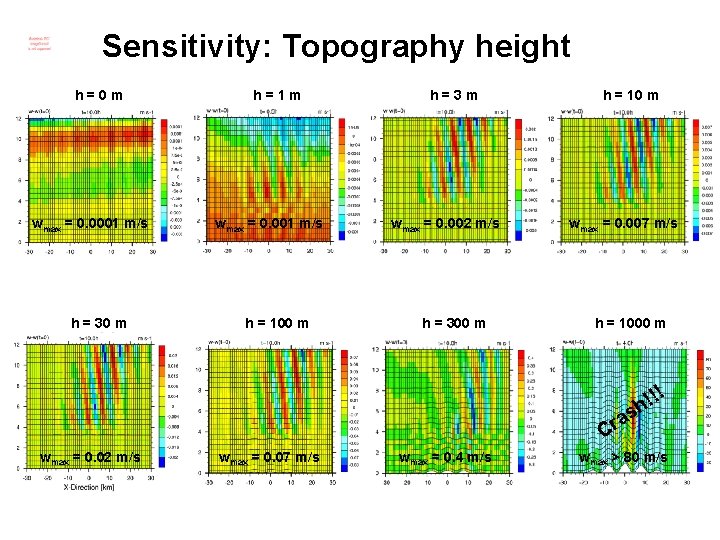
Ideal test case II • 2 -dimensional • Schaer et al. MWR 2002 topography • Gal-Chen coordinates • ∆x = 1 km Lx = 301 km • ∆z = 500 m Lz = 22. 5 km • ∆t = 25 s • Constant static stability frequency N = 0. 01 s-1 • Tropopause at 11 km • Rayleight sponge (> 12 km) l 2 tls =. true. irunge_kutta = 1 irk_order = 3 iadv_order = 5 lsl_adv_qx =. true. lva_impl_dyn =. true. ieva_order = 3

Sensitivity: Topography height h=0 m wmax = 0. 0001 m/s h = 30 m h=1 m wmax = 0. 001 m/s h = 100 m h=3 m wmax = 0. 002 m/s h = 300 m h = 10 m wmax = 0. 007 m/s h = 1000 m !! ! h as r C wmax = 0. 02 m/s wmax = 0. 07 m/s wmax = 0. 4 m/s wmax > 80 m/s

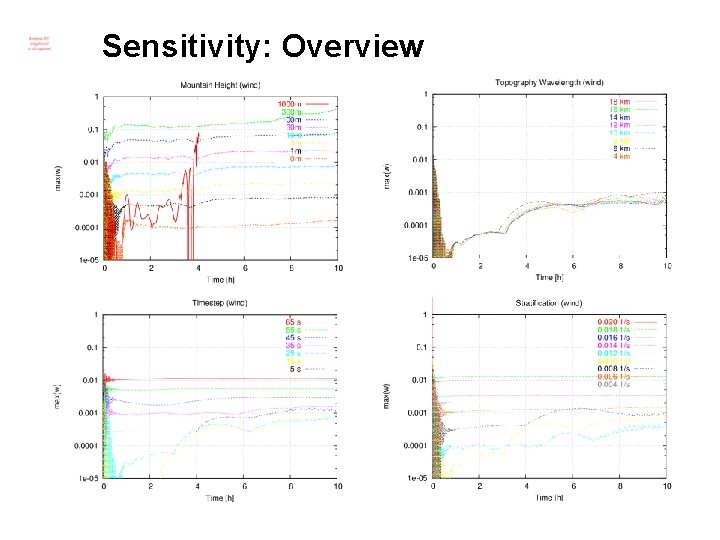
Sensitivity: Overview

Explanation • Advection of intensive quantity • Theoretical analysis of trunction error

Explanation • Upstream advection • Centered advection • Error term solely due to transformation • Linear in h 0 and u

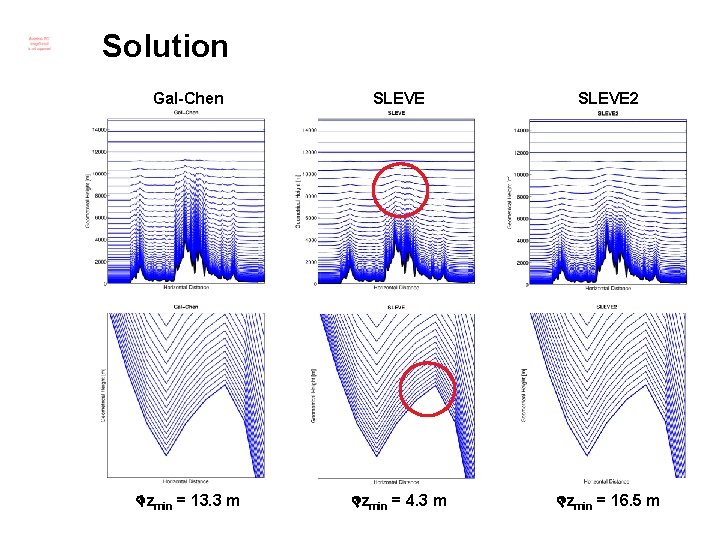
Solution Gal-Chen SLEVE 2 zmin = 13. 3 m zmin = 4. 3 m zmin = 16. 5 m

SLEVE 2 formulation • Gal-Chen coordinate • SLEVE 2 coordinate • Many parameters! How to choose?

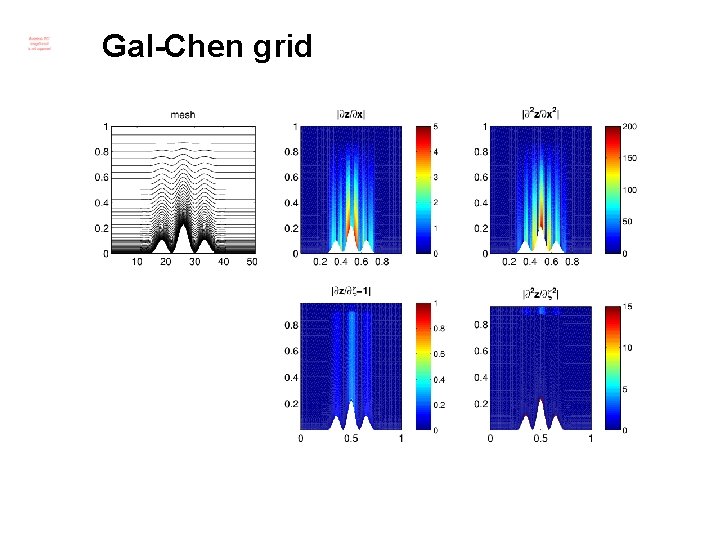
Criteria from numerics. . . • Local truncation error is a function of metric terms. . . • . . . and their derivatives

Gal-Chen grid

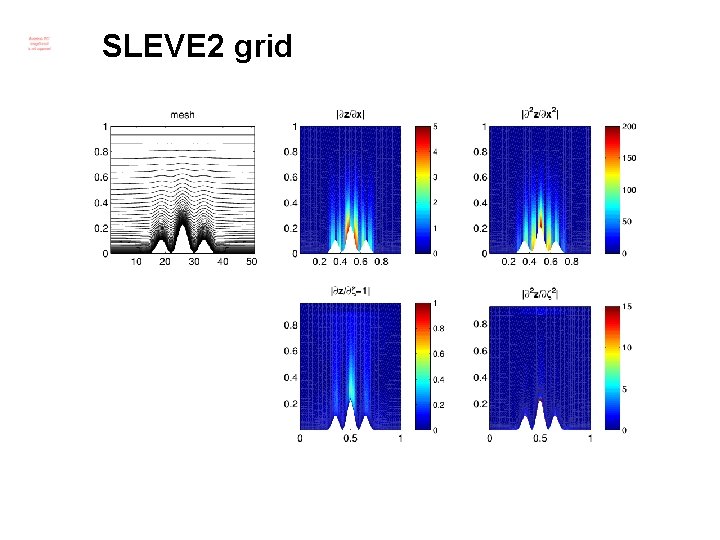
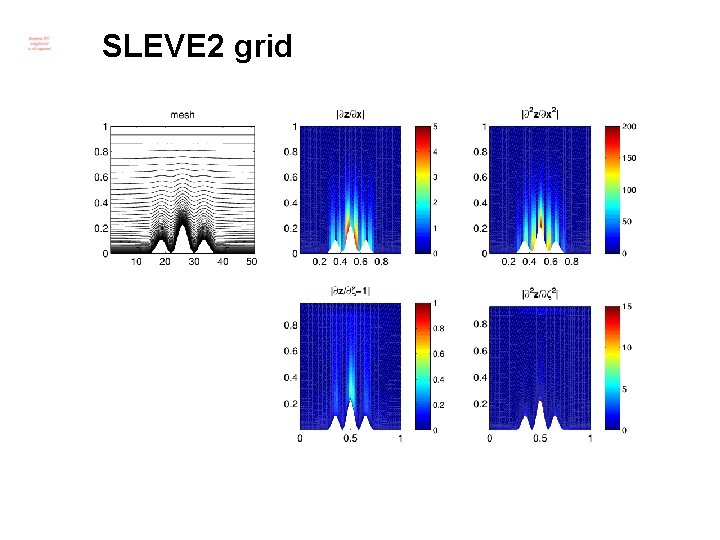
SLEVE 2 grid

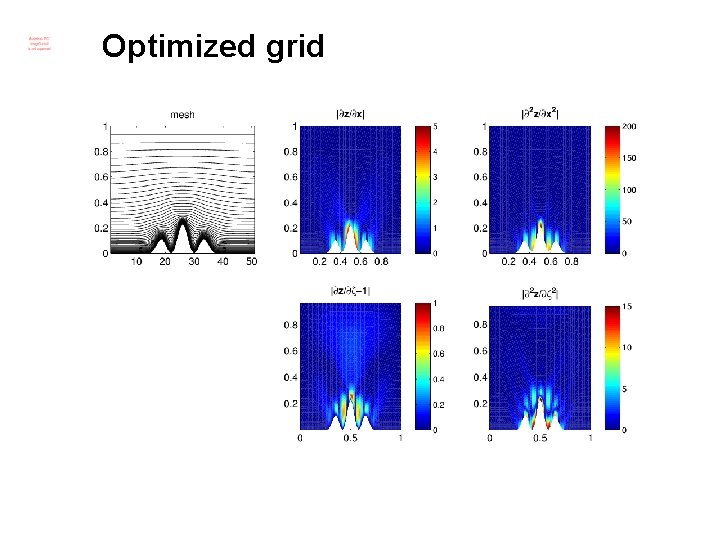
Optimal grid? • Optimize cost function • We have neglected cross-derivatives • Using n=2 for simplicity • Choose weights i inspired from SLEVE 2 values

Optimized grid

SLEVE 2 grid

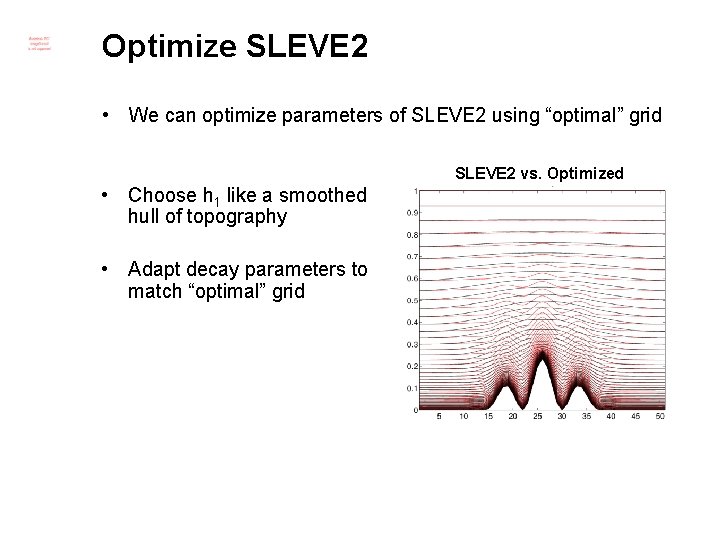
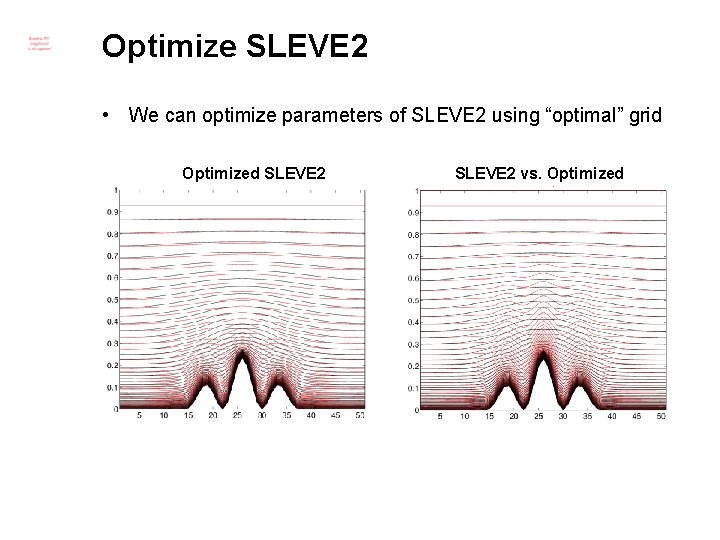
Optimize SLEVE 2 • We can optimize parameters of SLEVE 2 using “optimal” grid SLEVE 2 vs. Optimized • Choose h 1 like a smoothed hull of topography • Adapt decay parameters to match “optimal” grid

Optimize SLEVE 2 • We can optimize parameters of SLEVE 2 using “optimal” grid Optimized SLEVE 2 vs. Optimized

Conclusions • COSMO shows considerable truncation errors in presence of steep and high topography • Both for atmosphere at rest and constant advection test cases • Better vertical coordinate transformations (SLEVE 2) may reduce the amplitude at higher levels • But they have many parameters to choose and effects near the landsurface can be critical • Grid-optimization with numerically motivated cost function. . . • may be a tool to choose parameters intelligently • may assist in formulation of new vertical coordinates • also relies on some tuning

Outlook • Test optimized SLEVE 2 coordinate with idealized test cases • Implement optimized SLEVE 2 coordinate operationally • Investigate source of error for atmosphere at rest case? • Behaviour of COSMO with respect to specific grid deformations could help determine weight’s of cost function • Extend study to different time and space differencing scheme’s
 Federal department of home affairs fdha
Federal department of home affairs fdha Federal department of home affairs fdha
Federal department of home affairs fdha Federal department of home affairs fdha
Federal department of home affairs fdha Vha directive 1123
Vha directive 1123 Fdha loan
Fdha loan Lara renew nursing license
Lara renew nursing license Department of commerce and consumer affairs
Department of commerce and consumer affairs Department of local affairs
Department of local affairs Hhs office of population affairs
Hhs office of population affairs Ntust gym
Ntust gym Apply harvard
Apply harvard Pengertian home care
Pengertian home care Perbedaan home care dan home visit
Perbedaan home care dan home visit Mobile home exchange
Mobile home exchange Unit 1 home sweet home
Unit 1 home sweet home Come home come home jesus is calling
Come home come home jesus is calling Oak springs rv park
Oak springs rv park What did you say
What did you say André fougeron
André fougeron She said that, home economics stands for the ideal home.
She said that, home economics stands for the ideal home. Home sweet home: survive
Home sweet home: survive Back of the house department in a hotel
Back of the house department in a hotel Front office section and function
Front office section and function Front office department responsibilities
Front office department responsibilities Mlos in front office
Mlos in front office















































