ELECE 4810 Metamaterials and Nanophotonics D Exercise 2









- Slides: 19

ELEC-E 4810 Metamaterials and Nanophotonics D Exercise 2 - Solutions

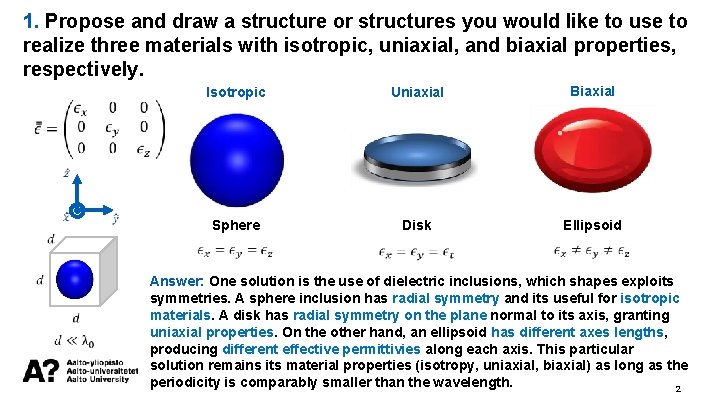
1. Propose and draw a structure or structures you would like to use to realize three materials with isotropic, uniaxial, and biaxial properties, respectively. Isotropic Uniaxial Biaxial Sphere Disk Ellipsoid Answer: One solution is the use of dielectric inclusions, which shapes exploits symmetries. A sphere inclusion has radial symmetry and its useful for isotropic materials. A disk has radial symmetry on the plane normal to its axis, granting uniaxial properties. On the other hand, an ellipsoid has different axes lengths, producing different effective permittivies along each axis. This particular solution remains its material properties (isotropy, uniaxial, biaxial) as long as the periodicity is comparably smaller than the wavelength. 2

3

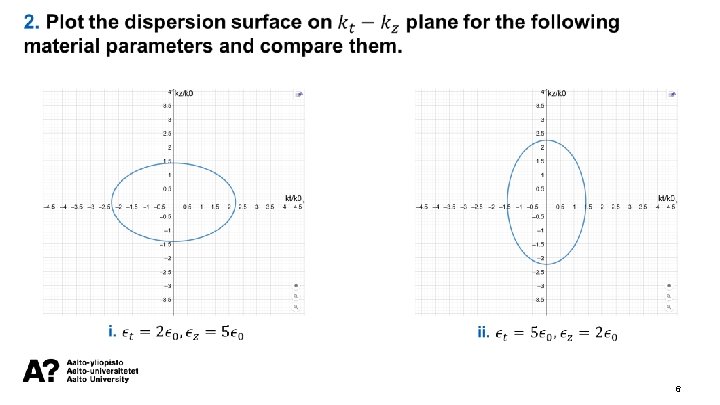
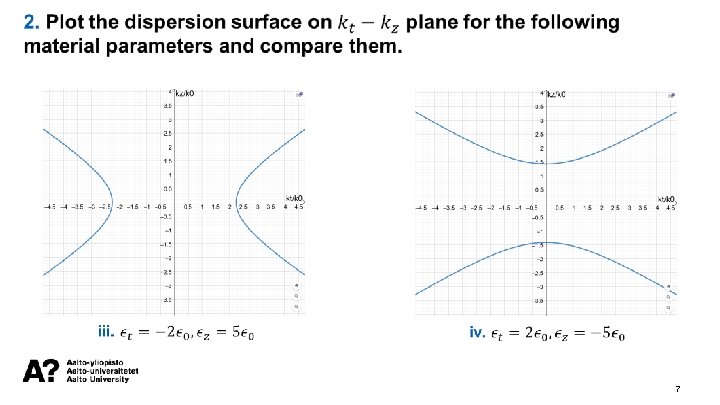
Dispersion diagrams What is the dispersion equation? Ordinary waves They define the eigenwaves, i. e. they give information how the waves propagate in the medium. Extraordinary waves Relation between the wavenumbers and the frequency 4

Dispersion diagrams 5

6

7

8

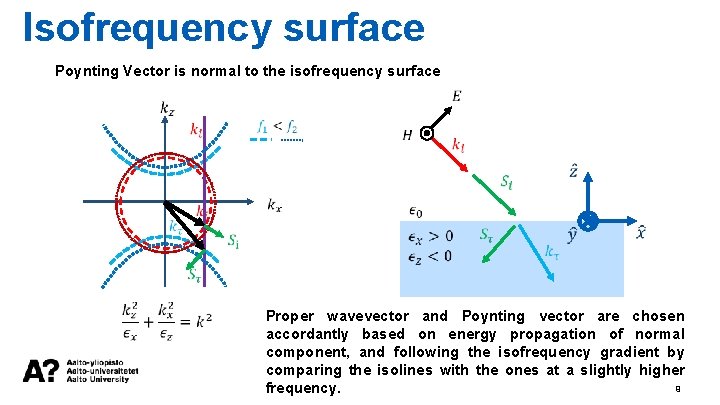
Isofrequency surface Poynting Vector is normal to the isofrequency surface Proper wavevector and Poynting vector are chosen accordantly based on energy propagation of normal component, and following the isofrequency gradient by comparing the isolines with the ones at a slightly higher 9 frequency.

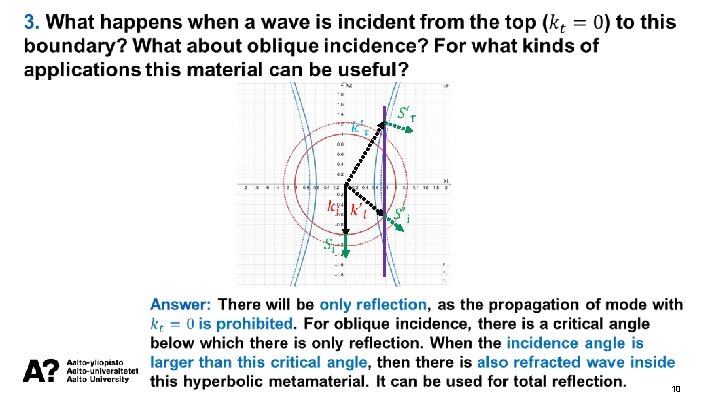
10

11

4. i. If the material has a non-linear response: Answer: This can be done by adding an additional non-linear component, for example 12

13

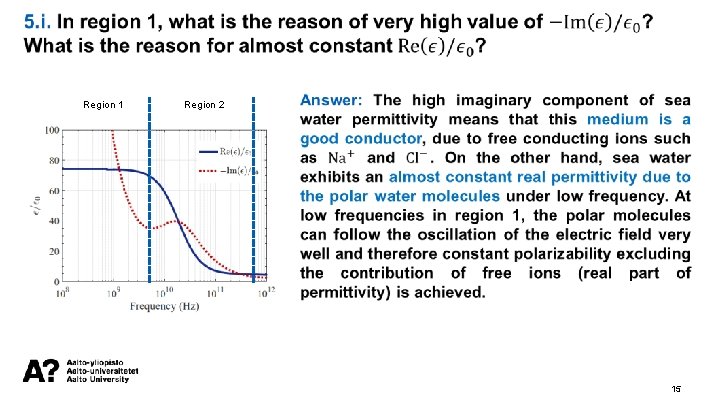
5. Look at the permittivity of seawater in the figure below and answer the following questions: Region 1 Region 3 Region 2 R. 4 R. 5 14

Region 1 Region 2 15

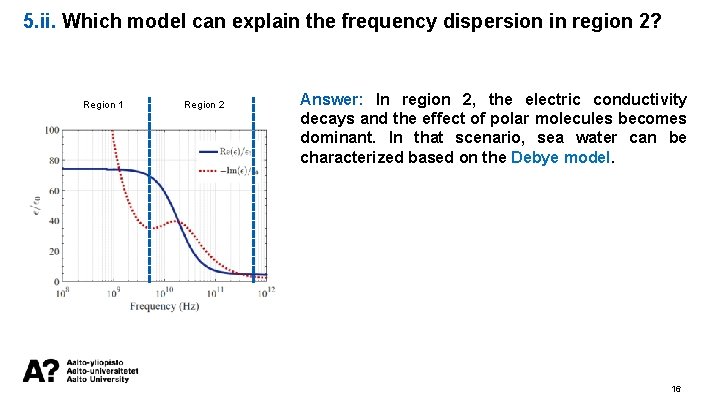
5. ii. Which model can explain the frequency dispersion in region 2? Region 1 Region 2 Answer: In region 2, the electric conductivity decays and the effect of polar molecules becomes dominant. In that scenario, sea water can be characterized based on the Debye model. 16

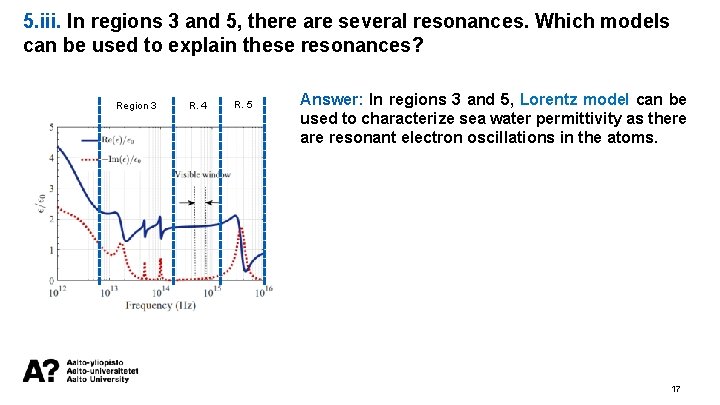
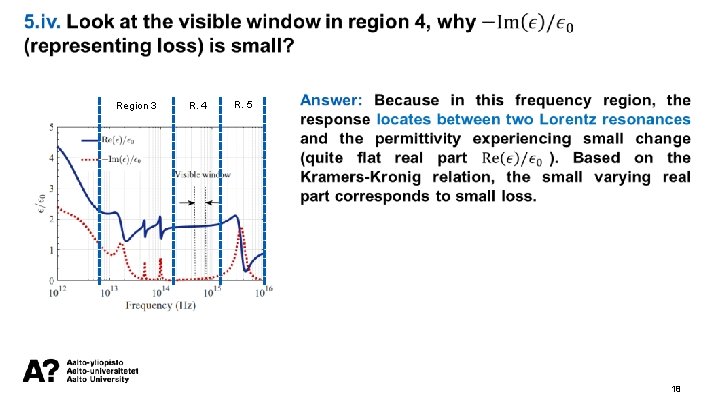
5. iii. In regions 3 and 5, there are several resonances. Which models can be used to explain these resonances? Region 3 R. 4 R. 5 Answer: In regions 3 and 5, Lorentz model can be used to characterize sea water permittivity as there are resonant electron oscillations in the atoms. 17

Region 3 R. 4 R. 5 18

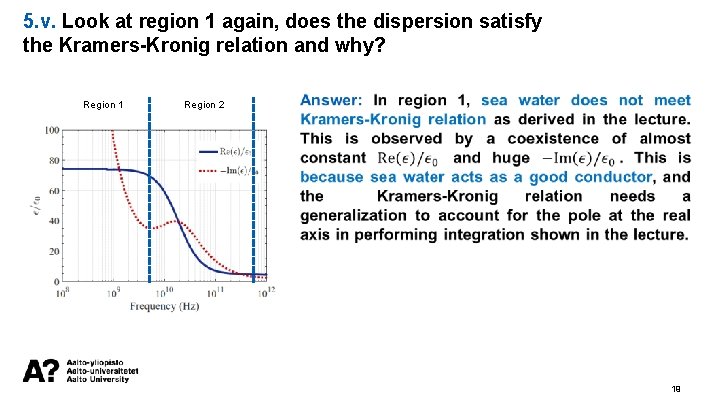
5. v. Look at region 1 again, does the dispersion satisfy the Kramers-Kronig relation and why? Region 1 Region 2 19
 Alexey belyanin
Alexey belyanin Applied nanophotonics
Applied nanophotonics Elen 4810
Elen 4810 Elen 4810
Elen 4810 Nanophotonics
Nanophotonics Sysc 4810
Sysc 4810 Lifelong fitness formula
Lifelong fitness formula Exercise past simple past continuous and past perfect
Exercise past simple past continuous and past perfect Ast levels and exercise
Ast levels and exercise Ib sehs topic 5
Ib sehs topic 5 Ib sports exercise and health science
Ib sports exercise and health science Appositive definition in literature
Appositive definition in literature Exercise physiology for health, fitness, and performance
Exercise physiology for health, fitness, and performance Hyperextension
Hyperextension Activity and exercise fundamentals of nursing
Activity and exercise fundamentals of nursing Textile machinery apush
Textile machinery apush Past simple and progressive exercises
Past simple and progressive exercises Physiology of sport and exercise 5th edition
Physiology of sport and exercise 5th edition Ib sports exercise and health science notes
Ib sports exercise and health science notes Ib sport exercise and health science
Ib sport exercise and health science





































