Ein Kartentrick und seine mathematischen Folgen KartentrickRahmen Gliederung

Ein Kartentrick und seine mathematischen Folgen Kartentrick/Rahmen

Gliederung ü Der Trick ü Das Mathematikseminar als Projektrahmen ü Der Projektablauf ü Die Ergebnisse ü Zusammenfassende Betrachtung ü Weiterführende Problemstellungen 1/13/2022 Kartentrick/Gliederung 2

Das Mathematikseminar ü I. Wahlkurs ü für interessierte Schüler. Innen (hier 6. - 8. Jgst. ) ü einstündig pro Woche ü Inhalte: ü Jahresthema (z. B. Mathematik und Spiele) ü Mathematikwettbewerbe (Mathematikolympiade; Känguru. . . ) 1/13/2022 Kartentrick/Rahmen R. Mertenbacher 3

Das Mathematikseminar Sterzing (Südtirol) ü II. Workshop ü Projektunterricht ü Wettbewerbstraining ü Ortserkundung 1/13/2022 Kartentrick/Rahmen R. Mertenbacher 4

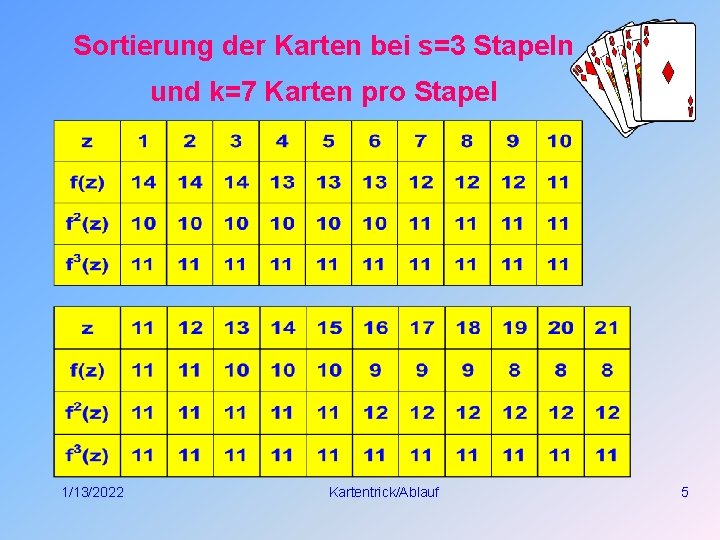
Sortierung der Karten bei s=3 Stapeln und k=7 Karten pro Stapel 1/13/2022 Kartentrick/Ablauf 5

Auftauchende Fragen (I) ü Geht der Trick auch mit einer anderen Karten - bzw. Stapelanzahl? ü Bleibt das Verfahren gleich? ü Auf welche Fixzahl stabilisiert sich jeweils das Verfahren? ü Wie viele Schritte sind nötig? 1/13/2022 Kartentrick/Ablauf 6

Bezeichnungen s = Stapelanzahl, ungerade, damit es einen mittleren Stapel gibt k = Kartenanzahl pro Stapel n = ks = Anzahl aller Karten z = Platznummer der Karte, die man sich merkt m = Anzahl der notwendigen Schritte bis der Trick beendet wird x = Fixzahl, d. h. Nummer des Platzes, auf dem letztlich alle Karten zu liegen kommen 1/13/2022 Kartentrick/Ablauf 7

Sortierung der Karten bei s=3 Stapeln und k=3 Karten pro Stapel 1/13/2022 Kartentrick/Ablauf 8

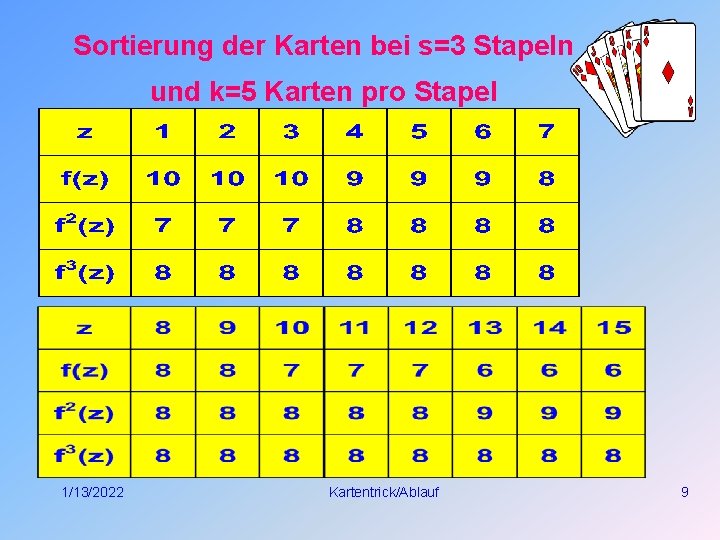
Sortierung der Karten bei s=3 Stapeln und k=5 Karten pro Stapel 1/13/2022 Kartentrick/Ablauf 9

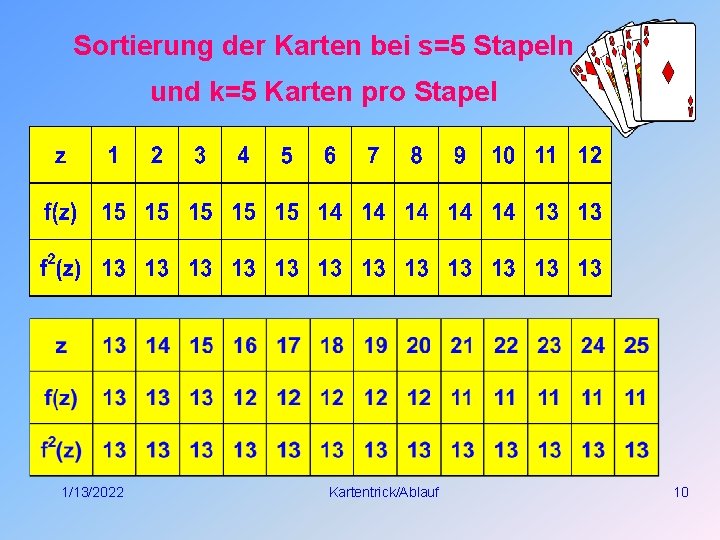
Sortierung der Karten bei s=5 Stapeln und k=5 Karten pro Stapel 1/13/2022 Kartentrick/Ablauf 10

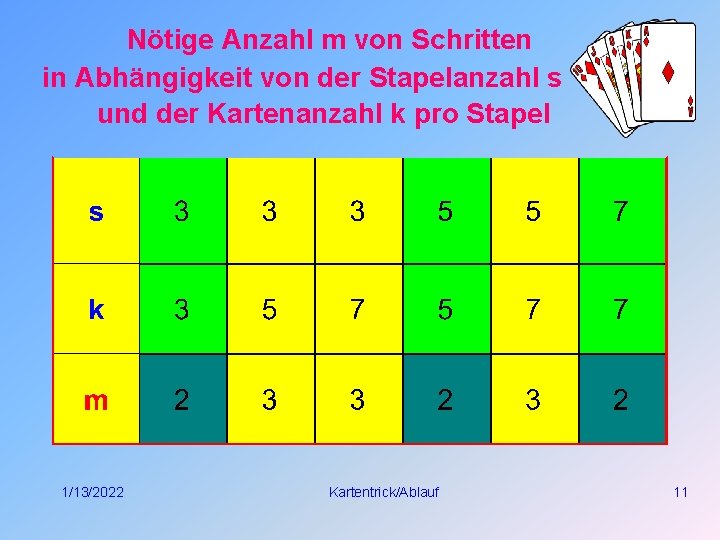
Nötige Anzahl m von Schritten in Abhängigkeit von der Stapelanzahl s und der Kartenanzahl k pro Stapel 1/13/2022 Kartentrick/Ablauf 11

Auftauchende Fragen (II) ü Muss k s sein? Vorsicht! ü Gilt immer x = 0, 5(sk + 1)? ü Ist m = 3, falls k > s und m = 2, falls k = s? Vorsicht! 1/13/2022 Kartentrick/Ablauf 12

Definition: <a> ist diejenige größte ganze Zahl, die kleiner a ist. Beispiele: <3, 5> = 3; <3> = 2; Bemerkung: <a> = [a] - [[a]: a] 1/13/2022 Kartentrick/Ablauf 13

Satz f(z) = 0, 5(s + 1)k - <z: s> für z {1; . . . ; n} 1/13/2022 Kartentrick/Ergebnisse 14

Hilfssatz Die Funktion mit der Gleichung f(z) = 0, 5(s + 1)k - <z: s>; z {1; . . . ; n} hat folgende Eigenschaften: a) f(x) = x für alle x = 0, 5(sk + 1) b) f(1) f(z) für alle z {1; . . . ; n} d) Für die Wertemenge W von f gilt: W = {0, 5(s - 1)k + 1; . . . ; 0, 5(s + 1)k} = = {0, 5(s - 1)k + 1; . . . ; 0, 5(s - 1)k + k} Daraus folgt: |W| = k c) f ist monoton fallend 1/13/2022 Kartentrick/Ergebnisse 15

Bemerkung 1 Ist s ungerade, i {1; 2; . . . ; s} und (z - i): s eine ganze Zahl, so gilt: (z - i): s = <z: s> 1/13/2022 Kartentrick/Ergebnisse 16

Bemerkung 2 Für ungerade k und s mit k 3 und s 3, sowie für p N gelten die Identitäten: a) <k: 2 + 1: 2 s> = (k - 1): 2 b) <1: s + (sp - k): 2> = (sp - k): 2 1/13/2022 Kartentrick/Ergebnisse 17

Hauptsatz Es sei n = sk ungerade mit den natürlichen Zahlen s 3 und k 3, außerdem sei f eine Funktion mit f: D = {1; . . . ; n} N z f(z) = 0, 5(s + 1)k - <z: s> Dann gilt: fm(z) = 0, 5(n + 1) für alle z D mit m = p+1, wobei p N so gewählt werden kann, dass sp - 1 < k sp. 1/13/2022 Kartentrick/Ergebnisse 18

Beispiel s = 11 Stapel k = 10001 Karten pro Stapel m=4+1=5 denn 1331 = 113 < 10001 < 114 = 14641 1/13/2022 Kartentrick/Ergebnisse 19

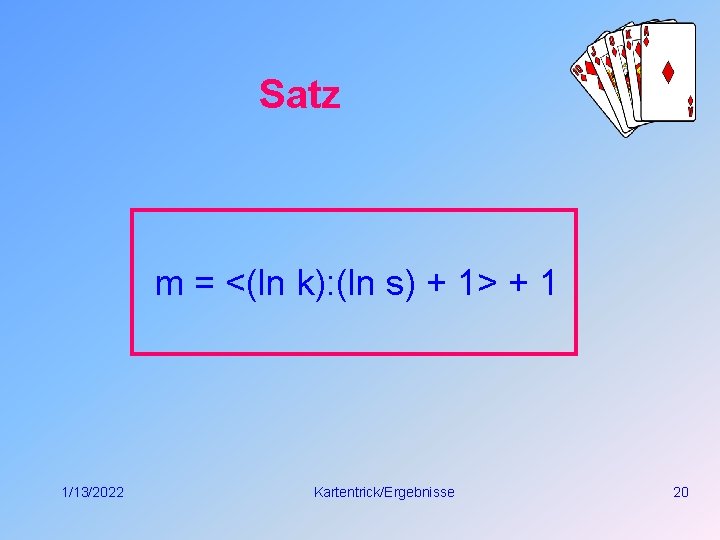
Satz m = <(ln k): (ln s) + 1> + 1 1/13/2022 Kartentrick/Ergebnisse 20

Vorgehensweise ü Problem in Zahlentabellen umsetzen! ü Erste Vermutungen anhand der Daten! Beweise? ü Gesetzmäßigkeiten bzw. Formeln ableiten! ü Größere Datenmengen mit PC-Unterstützung analysieren! ü Mathematisch exakte Beweise sind zu führen! 1/13/2022 Kartentrick/Zusammenfassung 21

Weitergehende Fragen ü Was passiert, wenn k gerade ist? ü Was passiert, wenn s gerade ist? ü Wie sieht das Verfahren aus, wenn nicht der mittlere Stapel gewählt wird? ü Gibt es auch ein Verfahren, wenn s nicht Teiler von n ist? 1/13/2022 Kartentrick/Weiterführung 22