Edge enhancement by linear and nonlinear filtering Dr

Edge enhancement by linear (and nonlinear) filtering Dr. Dileepan Joseph Dept. of Engineering Science University of Oxford, UK

Objectives n n Learn what edge enhancement is, why it is useful & how it differs from edge detection Define linear and nonlinear spatial filtering Design linear filters to either smoothen or sharpen the edges in an image and show the two operations are related Appreciate that human vision enhances edges using local operations

Edge enhancement n n The purpose of edge enhancement is to highlight fine detail in an image or to restore, at least partially, detail that has been blurred (either in error or as a consequence of a particular method of image acquisition) Applications of edge enhancement include electronic printing, medical imaging, industrial inspection, and autonomous target detection in smart weapons

Edge enhancement n n n Edge enhancement involves sharpening the outlines of objects and features with respect to their background Edge detection involves isolating the outlines of objects and features The former is easier to do than the latter

Spatial filtering n n n Image processing in the spatial domain may be expressed as g(x, y) = H{f(x, y)} where f is the input image, g is the output image, and H is an operator on f, defined over some neighbourhood of pixel (x, y)

Spatial filtering n n The neighbourhood of pixel (x, y), for image f, may be expressed as a column vector w(x, y) of pixel values e. g. Consider a 3 by 3 square neighbourhood centred on the pixel (x, y) of interest

Spatial filtering n A spatial filter H is linear if (and only if) q q n n H{a∙f(x, y)} = a∙H{f(x, y)} H{f 1(x, y)+f 2(x, y)} = H{f 1(x, y)}+H{f 2(x, y)} For any linear spatial filter H, we may write g(x, y) = h • w(x, y) where g is the output image, w is the neighbourhood vector of the input image f, and • is the inner product operator The column vector h is called a mask and it defines the properties of the linear filter

Spatial filtering n n It is easier to visualize linear spatial filtering as an inner product of h and w over the shape of the neighbourhood e. g. For a 3 by 3 square neighbourhood centred on the pixel (x, y) of interest g(x, y) = h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h 9 = h 1 w 1+h 2 w 2…+h 9 w 9 • w 1 w 2 w 3 w 4 w 5 w 6 w 7 w 8 w 9 f(x, y)

Smoothing filter n n To understand how to sharpen edges, we first consider how to smoothen them The simplest way to smoothen an image f is to use the neighbourhood average of pixel values to define the image g g(x, y) = 1/9 1/9 1/9 • w 1 w 2 w 3 w 4 w 5 w 6 w 7 w 8 w 9 f(x, y)

Smoothing filter n Middle region of the original image: 8 9 10 10 10 n 9 11 13 19 39 83 127 160 124 93 58 34 23 17 16 15 14 14 13 14 Middle region of the smoothed image: 9 10 11 14 20 35 48 54 53 47 52 58 59 56 49 57 59 58 53 41 33 23 19 16 16

Embossing filter n n Compared to the original image, edges in the smoothed image are slightly blurred Thus, the difference between the original and smooth images, which may be derived by spatial filtering, holds edge information − 1/9 g(x, y) = − 1/9 8/9 − 1/9 • w 1 w 2 w 3 w 4 w 5 w 6 w 7 w 8 w 9 f(x, y)

Embossing filter n Middle region of the original image: 8 9 10 10 10 n 9 11 13 19 39 83 127 160 124 93 58 34 23 17 16 15 14 14 13 14 Middle region of the embossed image: -1 -1 -1 -4 -10 -26 -37 -41 -34 -8 31 69 101 68 44 1 -25 -36 -25 -18 -9 -5 -3 -2

Sharpening filter n n The embossed image holds edge information over a uniform (zero) background Thus, the sum of the original and embossed images, which may be derived by spatial filtering, will reinforce edges of the former − 1/9 g(x, y) = − 1/9 17/9 − 1/9 • w 1 w 2 w 3 w 4 w 5 w 6 w 7 w 8 w 9 f(x, y)

Sharpening filter n Middle region of the original image: 8 9 10 10 10 n 9 11 13 19 39 83 127 160 124 93 58 34 23 17 16 15 14 14 13 14 Middle region of the sharpened image: 7 8 9 6 0 0 0 31 114 196 255 192 137 59 9 0 0 5 9 10 12

Edge enhancement n Without amplification: Emboss = Original − Smooth Sharp = Original + Emboss = 2∙Original − Smooth n With amplification A: Sharp = Original + A∙Emboss = (1+A)∙Original − A∙Smooth n e. g. Consider the mask h of a 3 by 3 square neighbourhood

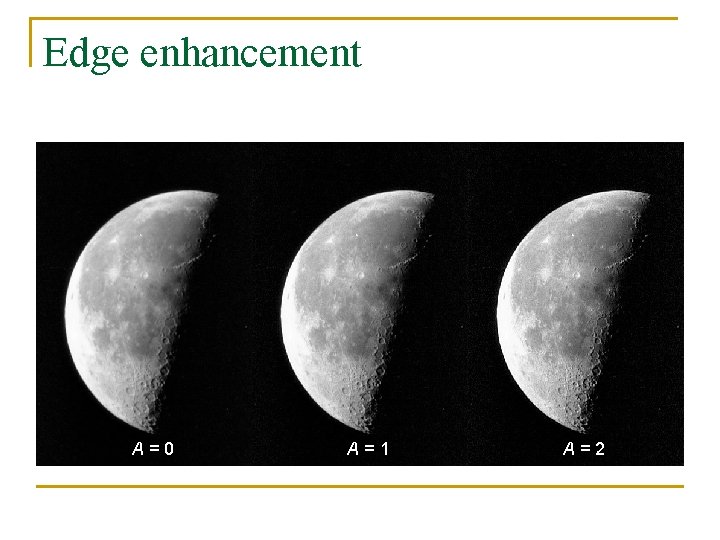
Edge enhancement A = 0 A = 1 A = 2

Mach Bands illusion n n This image has three sections: on the left, luminance is at a constant high; on the right, luminance is at a constant low; in the middle, it declines at a constant rate The thin bands seen on either side of the ramp (and named after their discoverer) are illusory

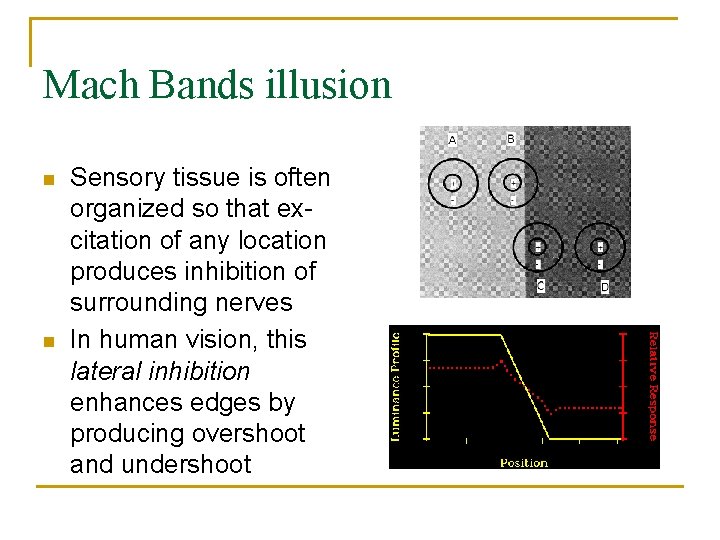
Mach Bands illusion n n Sensory tissue is often organized so that excitation of any location produces inhibition of surrounding nerves In human vision, this lateral inhibition enhances edges by producing overshoot and undershoot

Review n n n Edge enhancement involves sharpening the outlines of objects and features in an image with respect to their background Image processing in the spatial domain may be expressed as g(x, y) = H{f(x, y)} where f is the input image, g is the output image, and H is a linear or nonlinear operator on f, defined over some neighbourhood of pixel (x, y) Linear filtering may be expressed by an inner product of a mask and the neighbourhood

Review n n n Smoothing of edges may be achieved by neighbourhood averaging Sharpening of edges may be achieved by subtracting a multiple, A, of the neighbourhood average from a larger multiple, 1+A, of the neighbourhood centre The Mach Bands illusion may be understood in terms of edge enhancement by lateral inhibition in human vision

Resources n n Gonzales and Woods, Digital Image Processing, Second Edition, Prentice Hall, 2002 (get the first two chapters free from http: //www. imageprocessingbook. com/) Matlab Image Processing Toolbox http: //www. cquest. utoronto. ca/psych/psy 280 f/ ch 3/mb/mb. html (Mach Bands illusion) http: //www. siggraph. org/education/materials/ Hyper. Vis/vision/latinib. htm (lateral inhibition)