DISPERSI RELATIF KECONDONGAN KURTOSIS Presented by Astuti Mahardika

DISPERSI RELATIF, KECONDONGAN & KURTOSIS Presented by Astuti Mahardika, M. Pd 1

Dispersi Relatif • Ukuran dispersi absolut (jangkauan, simpangan rata-rata, simpangan kuartil, simpangan baku) hanya dapat mendeskripsikan variasi nilai pada satu kumpulan data bukan beberapa kumpulan data • Ukuran dispersi relatif dapat digunakan untuk membandingkan variasi nilai pada beberapa kumpulan data 2

Dispersi Relatif • Koefisien Variasi • Variasi Jangkauan • Variasi Simpangan Rata-rata • Variasi Kuartil 3

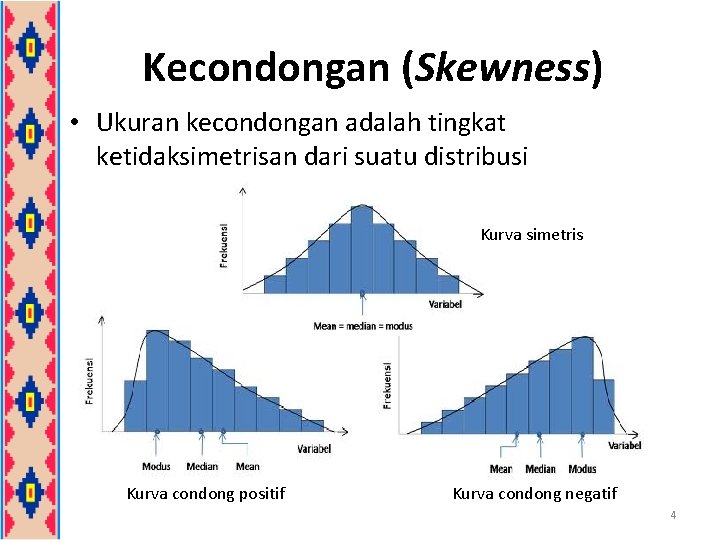
Kecondongan (Skewness) • Ukuran kecondongan adalah tingkat ketidaksimetrisan dari suatu distribusi Kurva simetris Kurva condong positif Kurva condong negatif 4

Kecondongan (Skewness) • Koefisien Kecondongan Pearson atau • Koefisien yang dihasilkan dari kedua rumus tersebut memiliki nilai yang hampir sama (dekat) karena rumus yang kedua dihasilkan dengan cara pendekatan bahwa 5

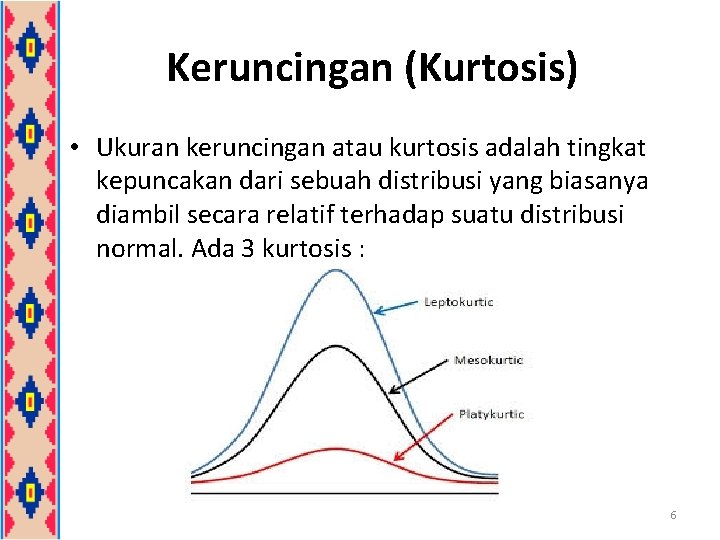
Keruncingan (Kurtosis) • Ukuran keruncingan atau kurtosis adalah tingkat kepuncakan dari sebuah distribusi yang biasanya diambil secara relatif terhadap suatu distribusi normal. Ada 3 kurtosis : 6

Keruncingan (Kurtosis) • Koefisien kurtosis dilambangkan 4 (alpha 4) • Kriteria distribusi: a. 4 < 3 maka distribusi platikurtik b. 4 = 3 maka distribusi mesokurtik c. 4 > 3 maka distribusi leptokurtik • Koefisien kurtosis: a. Data tunggal: b. Data kelompok 7

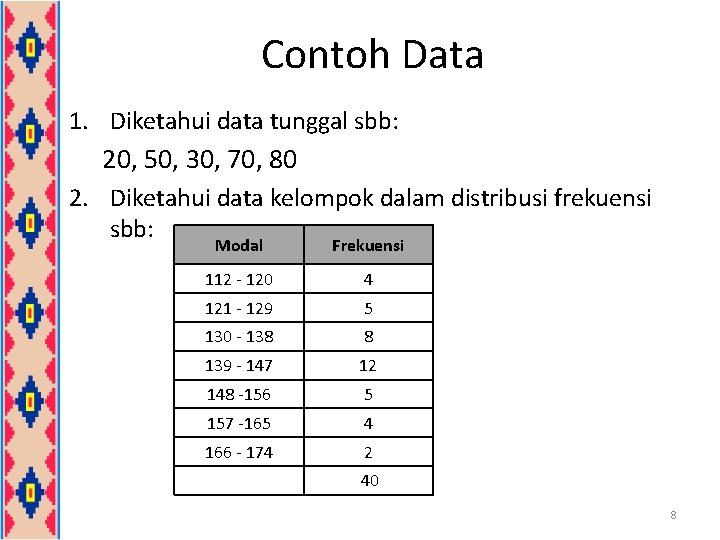
Contoh Data 1. Diketahui data tunggal sbb: 20, 50, 30, 70, 80 2. Diketahui data kelompok dalam distribusi frekuensi sbb: Modal Frekuensi 112 - 120 4 121 - 129 5 130 - 138 8 139 - 147 12 148 -156 5 157 -165 4 166 - 174 2 40 8

1. Diketahui data tunggal sbb: 20, 50, 30, 70, 80 20, 30, 50, 70, 80 Dari perhitungan pertemuan sebelumnya diperoleh : Mean = 50 , Me = 50, s = 25, 5 Berdasarkan koefisien kecondongannya termasuk dalam distribusi kurva simetris 9

1. Diketahui data tunggal sbb: 20, 50, 30, 70, 80 20, 30, 50, 70, 80 Dari perhitungan pertemuan sebelumnya diperoleh Mean = 50 , Me = 50, s = 25, 5 X X-X (X-X)4 20 -30 810000 30 -20 160000 50 0 0 70 20 160000 80 30 810000 Sigma 1940000 Berdasarkan koefien kurtosis disimpulkan bahwa termasuk kurva distribusi platikurtik 10

2. Data kelompok dalam distribusi frekuensi : Dari perhitungan pertemuan sebelumnya diketahui: mean = 140, 5 dan s = 14, 2 Modal Frekuensi • Dihitung dahulu Mo atau Me 112 - 120 4 • Kemudian cari sk dengan: 121 - 129 5 atau 130 - 138 8 139 - 147 12 148 -156 5 157 -165 4 166 - 174 2 40 • Simpulkan kecondongan kurva berdasarkan sk tersebut 11

2. Data kelompok dalam distribusi frekuensi : Dari perhitungan pertemuan sebelumnya diketahui: mean = 140, 5 dan s = 14, 2 Modal X Frekuensi 112 - 120 4 121 - 129 5 130 - 138 8 139 - 147 12 148 -156 5 157 -165 4 166 - 174 2 40 Dari hasil perhitungan tabel cari kemudian disimpulkan kategori kurtosisnya 12

13