Deriving the Range Equation Ground to Ground Launches

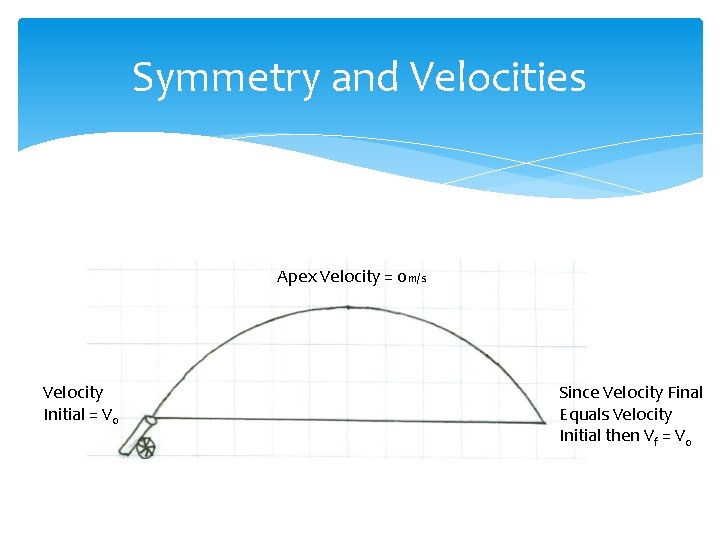
Deriving the Range Equation Ground to Ground Launches This works for ground to ground launches only. This derivation uses the principle of symmetry ( what goes up must come down) This derivation is based on the principle that the initial velocity going up will have a negative acceleration until it reaches the paths apex with a velocity of zero The projectile will then accelerate due to gravity until it reaches the ground at a velocity equal to the initial velocity.

Symmetry and Velocities Apex Velocity = 0 m/s Velocity Initial = V 0 Since Velocity Final Equals Velocity Initial then Vf = V 0

Velocity Vector Direction Changes or What Goes Up Must Come Down • In the picture below, the equal in magnitude and opposite in direction velocity vectors are shown as V 0 • The horizontal range is shown as ΔX • The angle of the launch (both assent and descent are shown as θ

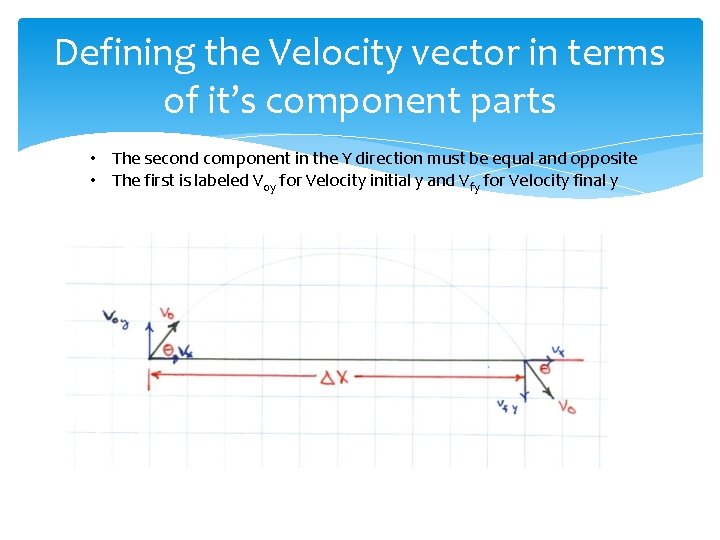
Defining the Velocity vector in terms of it’s component parts • If V 0 is treated as the resultant vector, It can be broken into it’s component parts as shown below in blue • Since horizontal velocity is constant then Vx initial = Vx final • There is never an acceleration in the X direction

Defining the Velocity vector in terms of it’s component parts • The second component in the Y direction must be equal and opposite • The first is labeled Voy for Velocity initial y and Vfy for Velocity final y

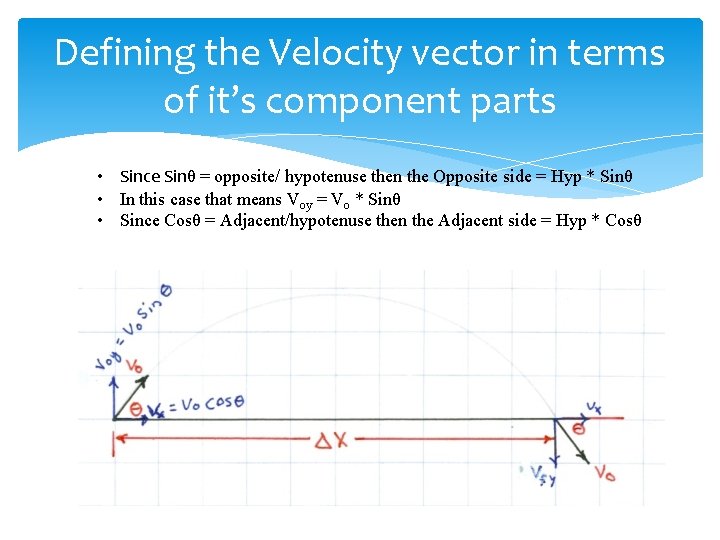
Defining the Velocity vector in terms of it’s component parts • Since Sinθ = opposite/ hypotenuse then the Opposite side = Hyp * Sinθ • In this case that means Voy = Vo * Sinθ • Since Cosθ = Adjacent/hypotenuse then the Adjacent side = Hyp * Cosθ

Defining the Velocity vector in terms of it’s component parts • Since Horizontal velocity is constant Vx final is the same as Vx initial • In other words Vx final is the same as saying Adjacent side = Hyp * Cosθ • Or Vx = V 0 Cos θ

Defining the Velocity vector in terms of it’s component parts • The Vertical velocity is equal in magnitude but opposite in direction • Vfy is the same as saying the negative of Opposite side = Hyp * Sinθ • Or Vfy = -V 0 Sin θ

Solving the problem The X direction Velocity = Distance / time Vx = Δx/ΔT Since Vx = V 0 Cosθ we can say V 0 Cosθ = Δx/ΔT Solving for time we can say ΔT = Δx/ V 0 Cosθ

Solving the problem The Y direction Typically when speaking of final velocity we have assumed an initial velocity of 0 m/s If that is true Final velocity is simply equal to Acceleration * change in time If our initial velocity is not zero we must add that to this equation and say Vfv = Vo + AΔT In our problem this means Vfv = Voy + AΔT Since Vfv is equal in magnitude but opposite in direction to V oy we can say – Voy = Voy + AΔT Going one step further since Voy = V 0 Sinθ We can substitute – V 0 Sinθ = V 0 Sinθ + AΔT

Combining Terms We now have – V 0 Sinθ = V 0 Sinθ + AΔT Subtract – V 0 Sinθ from both sides we get – 2 V 0 Sinθ = AΔT

Combining Equations From our X direction equation we can substitute for ΔT where ΔT = ΔX/ V 0 Cosθ So – 2 V 0 Sinθ = A(ΔX/ V 0 Cosθ) Now solve for ΔX the range ΔX = – 2 V 20 Sinθ Cosθ A

Trigonometry Identities From Trigonometry we remember 2 Sinθ Cos θ = Sin 2θ Therefore we can substitute and get ΔX = - V 20 Sin 2θ/A Where ΔX = the range

Final Formula The Initial Velocity (v 0) will always be a positive number When the opposite of a positive number is squared Example - V 20 The result is V 20 This leaves a final formula of ΔX = V 20 Sin 2θ/A Where ΔX = the range