Department of Mathematics Maheshtala college NewtonRaphson Iteration Presented

  • Slides: 21
Download presentation
Department of Mathematics Maheshtala college Newton-Raphson Iteration Presented by Ajijur Rahaman Mallick

Department of Mathematics Maheshtala college Newton-Raphson Iteration Presented by Ajijur Rahaman Mallick

Newton-Raphson Iteration It isn’t always possible to find iterative formulae of the type that

Newton-Raphson Iteration It isn’t always possible to find iterative formulae of the type that will find the solution of every equation. Another iterative method that is useful is called the Newton-Raphson method.

Newton-Raphson Iteration Suppose we want to find an approximate solution to the equation To

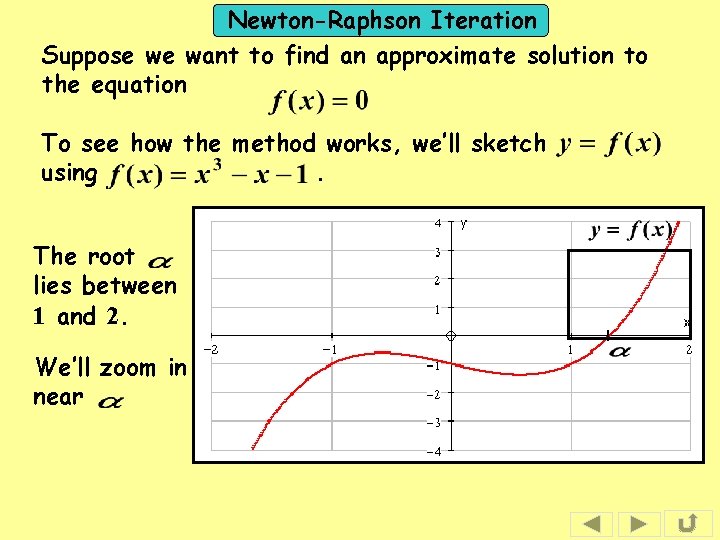
Newton-Raphson Iteration Suppose we want to find an approximate solution to the equation To see how the method works, we’ll sketch using. The root lies between 1 and 2. We’ll zoom in near

Newton-Raphson Iteration Suppose our first estimate is given by. We draw the tangent to

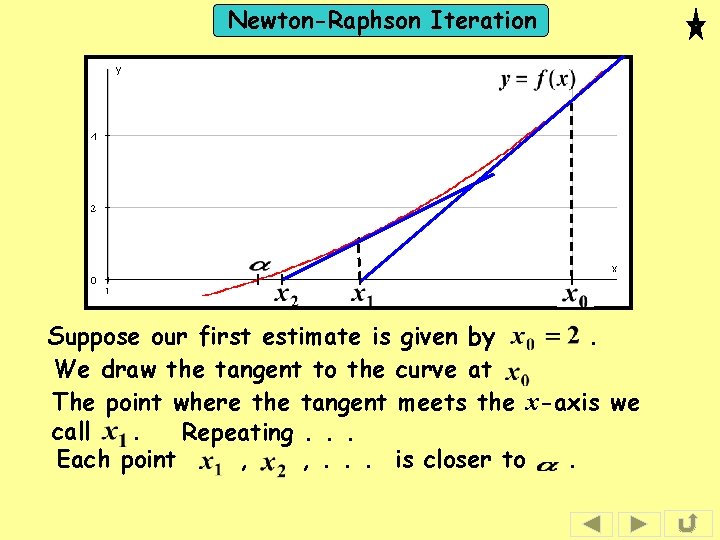
Newton-Raphson Iteration Suppose our first estimate is given by. We draw the tangent to the curve at The point where the tangent meets the x-axis we call. Repeating. . . Each point , , . . . is closer to.

Newton-Raphson Iteration To carry out the iteration we need to find the points where

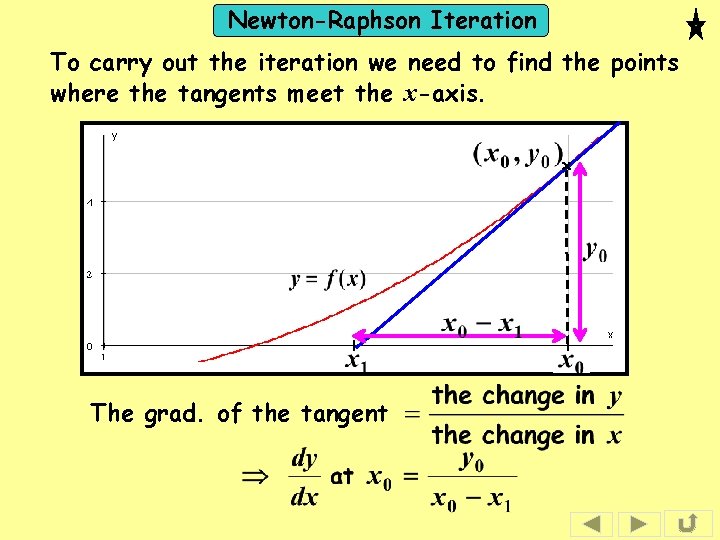
Newton-Raphson Iteration To carry out the iteration we need to find the points where the tangents meet the x-axis. x The grad. of the tangent

Newton-Raphson Iteration We have Using and we need to find and in the formula

Newton-Raphson Iteration We have Using and we need to find and in the formula isn’t very convenient, so, since we have and Then, Rearranging: .

Newton-Raphson Iteration So, We just need to alter the subscripts to find : Generalising

Newton-Raphson Iteration So, We just need to alter the subscripts to find : Generalising gives We don’t need a diagram to use this formula but we must know how to differentiate. Convergence is often very fast.

Newton-Raphson Iteration e. g. Use the Newton-Raphson method with to find the root of

Newton-Raphson Iteration e. g. Use the Newton-Raphson method with to find the root of the equation correct to 4 d. p. Solution: Let Differentiate: Using a calculator we need: Then,

Newton-Raphson Iteration SUMMARY To use the Newton-Raphson method to estimate a root of an

Newton-Raphson Iteration SUMMARY To use the Newton-Raphson method to estimate a root of an equation: Ø rearrange the equation into the form Ø differentiate Ø substitute to find and into the formula Ø choose a suitable starting value for Ø use a calculator to iterate Tip: It saves a lot of errors if, before you type the formula into your calculator, you write the formula with ANS replacing every x.

Exercise Newton-Raphson Iteration 1. (a) Use the Newton-Raphson method to estimate the root of

Exercise Newton-Raphson Iteration 1. (a) Use the Newton-Raphson method to estimate the root of the following equation to 6 d. p. using the starting value given: (b) What happens if you use ? (c) Use your calculator or a graph plotter to sketch the graph of. (d) What is special about the graph at and why does it explain the answer to (b) ? 2. Use the Newton-Raphson method to estimate one root of to 4 d. p. using

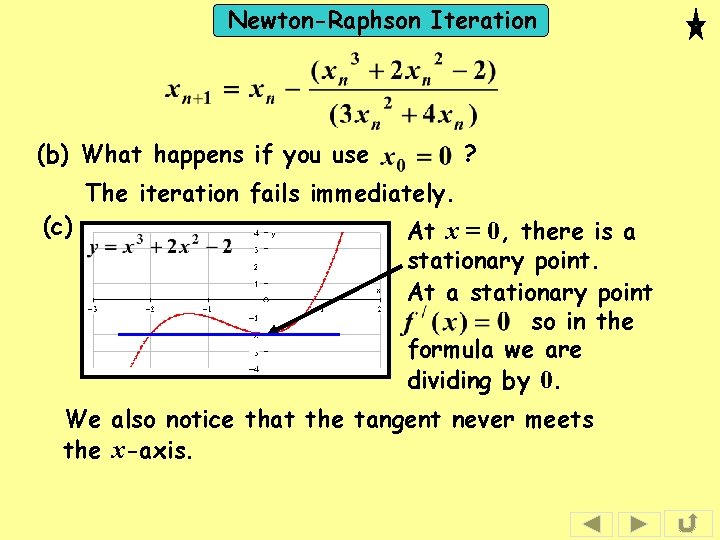
Newton-Raphson Iteration (a) Solution: Let

Newton-Raphson Iteration (a) Solution: Let

Newton-Raphson Iteration (b) What happens if you use (c) ? The iteration fails immediately.

Newton-Raphson Iteration (b) What happens if you use (c) ? The iteration fails immediately. At x = 0, there is a stationary point. At a stationary point so in the formula we are dividing by 0. We also notice that the tangent never meets the x-axis.

Newton-Raphson Iteration 2. Use the Newton-Raphson method to estimate one root of to 4

Newton-Raphson Iteration 2. Use the Newton-Raphson method to estimate one root of to 4 d. p. using Solution: Let Radians!

Newton-Raphson Iteration The Newton-Raphson method will fail if Ø i. e. at a stationary

Newton-Raphson Iteration The Newton-Raphson method will fail if Ø i. e. at a stationary point It will also sometimes fail to give the expected root if the initial value is close to a stationary point. Can you draw a graph to show what could happen in this case? This is one example.

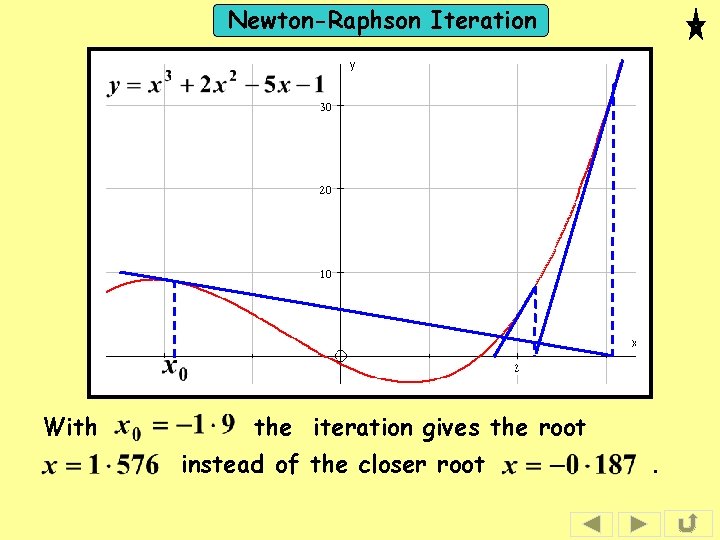
Newton-Raphson Iteration With the iteration gives the root instead of the closer root .

Newton-Raphson Iteration With the iteration gives the root instead of the closer root .

Newton-Raphson Iteration

Newton-Raphson Iteration

Newton-Raphson Iteration The following slides contain repeats of information on earlier slides, shown without

Newton-Raphson Iteration The following slides contain repeats of information on earlier slides, shown without colour, so that they can be printed and photocopied. For most purposes the slides can be printed as “Handouts” with up to 6 slides per sheet.

Newton-Raphson Iteration It isn’t always possible to find iterative formulae of the type that

Newton-Raphson Iteration It isn’t always possible to find iterative formulae of the type that will find the solution of every equation. Another iterative method that is useful is called the Newton-Raphson method.

Newton-Raphson Iteration SUMMARY To use the Newton-Raphson method to estimate a root of an

Newton-Raphson Iteration SUMMARY To use the Newton-Raphson method to estimate a root of an equation: Ø rearrange the equation into the form Ø differentiate Ø substitute to find and into the formula Ø choose a suitable starting value for Ø use a calculator to iterate Tip: It saves a lot of errors if, before you type the formula into your calculator, you write the formula with ANS replacing every x.

Newton-Raphson Iteration e. g. Use the Newton-Raphson method with to find the root of

Newton-Raphson Iteration e. g. Use the Newton-Raphson method with to find the root of the equation correct to 4 d. p. Solution: Let Differentiate: Using a calculator we need: Then,

Newton-Raphson Iteration The Newton-Raphson method will fail if Ø i. e. at a stationary

Newton-Raphson Iteration The Newton-Raphson method will fail if Ø i. e. at a stationary point It will also sometimes fail if the initial value is close to a stationary point.

Department of Mathematics Maheshtala College Rolles Theorem andDepartment of Mathematics Maheshtala College Rolles Theorem and
Department of Mathematics Maheshtala College Subgroups and CyclicDepartment of Mathematics Maheshtala College Subgroups and Cyclic
DEPARTMENT OF MATHEMATICS Maheshtala College Systems of LinearDEPARTMENT OF MATHEMATICS Maheshtala College Systems of Linear
NewtonRaphson Method 1 NewtonRaphson Method Figure 1 GeometricalNewtonRaphson Method 1 NewtonRaphson Method Figure 1 Geometrical
NewtonRaphson Method http numericalmethods eng usf edu NewtonRaphsonNewtonRaphson Method http numericalmethods eng usf edu NewtonRaphson
Processes Sujata Ray Dey Maheshtala College Computer ScienceProcesses Sujata Ray Dey Maheshtala College Computer Science
T76 4115 Iteration demo T76 4115 Iteration DemoT76 4115 Iteration demo T76 4115 Iteration Demo
11 iteration ALI Accelerated Lambda Iteration Variable Eddington11 iteration ALI Accelerated Lambda Iteration Variable Eddington
T76 4115 Iteration demo T76 4115 Iteration DemoT76 4115 Iteration demo T76 4115 Iteration Demo
Iteration Chapters 6 7 Iteration in LISP unlikeIteration Chapters 6 7 Iteration in LISP unlike
Java iteration statements Iteration statements are statements whichJava iteration statements Iteration statements are statements which
Iteration 2 GRASP MORE PATTERNS xuyingxiao126 com ITERATIONIteration 2 GRASP MORE PATTERNS xuyingxiao126 com ITERATION
T76 4115 Iteration Demo Apollo Crew PP IterationT76 4115 Iteration Demo Apollo Crew PP Iteration
Iteration Chapter 21 Iteration Repetition 2 Looping ViaIteration Chapter 21 Iteration Repetition 2 Looping Via
T76 4115 Iteration demo T76 4115 Iteration DemoT76 4115 Iteration demo T76 4115 Iteration Demo
Sprint Review Iteration Meeting ddmonthyyyy Your name IterationSprint Review Iteration Meeting ddmonthyyyy Your name Iteration
Loop Statements Iteration Iteration o A portion ofLoop Statements Iteration Iteration o A portion of
Chapter 6 Iteration Chapter 6 Iteration 1 ChapterChapter 6 Iteration Chapter 6 Iteration 1 Chapter
Elaboration Iteration 3 popo Elaboration Iteration 3 BasicsElaboration Iteration 3 popo Elaboration Iteration 3 Basics
Iteration Statements Iteration Statements Loop structures allows aIteration Statements Iteration Statements Loop structures allows a