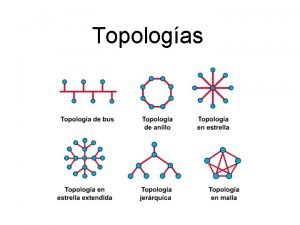
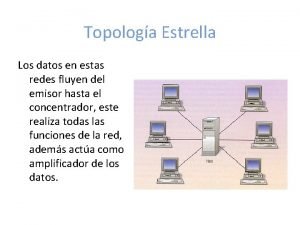
Departamento de Geometra y Topologa Facultad de Ciencias

Departamento de Geometría y Topología Facultad de Ciencias Matemáticas Universidad Complutense de Madrid APLICACIONES DE LA TEORIA DE MORSE Y DE LA CIRUGIA AL ESTUDIO DE HIPERSUPERFICIES Y VARIEDADES DE DIMENSION BAJA Memoria presentada por Pedro María González Manchón para optar al grado de Doctor en Ciencias Matemáticas Dirigida por el Profesor D. Enrique Outerelo Domínguez Departamento de Geometría y Topología Facultad de Ciencias Matemáticas Universidad Complutense de Madrid, Junio de 1. 996

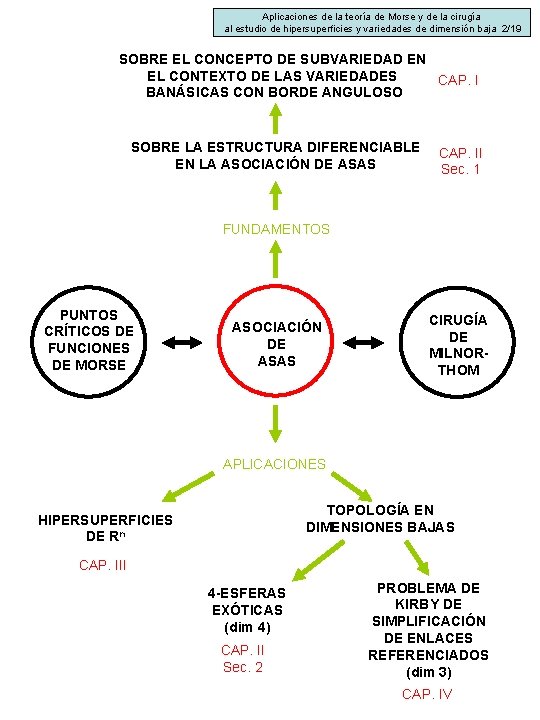
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 2/19 SOBRE EL CONCEPTO DE SUBVARIEDAD EN EL CONTEXTO DE LAS VARIEDADES CAP. I BANÁSICAS CON BORDE ANGULOSO SOBRE LA ESTRUCTURA DIFERENCIABLE EN LA ASOCIACIÓN DE ASAS CAP. II Sec. 1 FUNDAMENTOS PUNTOS CRÍTICOS DE FUNCIONES DE MORSE ASOCIACIÓN DE ASAS CIRUGÍA DE MILNORTHOM APLICACIONES TOPOLOGÍA EN DIMENSIONES BAJAS HIPERSUPERFICIES DE Rn CAP. III 4 -ESFERAS EXÓTICAS (dim 4) CAP. II Sec. 2 PROBLEMA DE KIRBY DE SIMPLIFICACIÓN DE ENLACES REFERENCIADOS (dim 3) CAP. IV

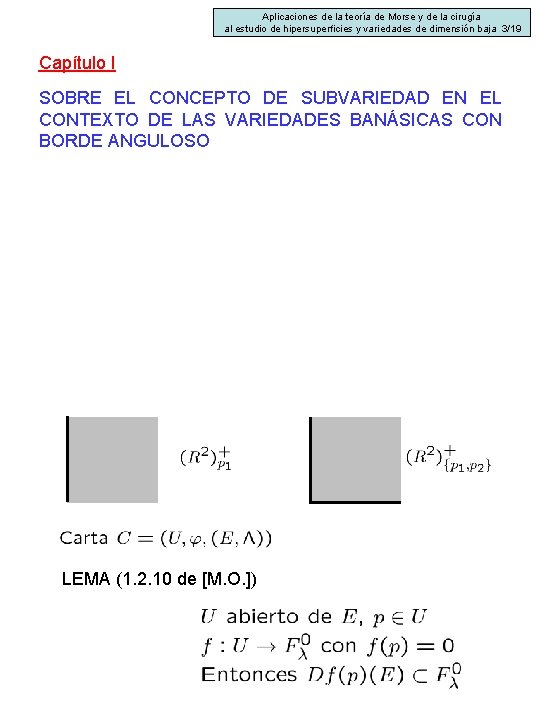
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 3/19 Capítulo I SOBRE EL CONCEPTO DE SUBVARIEDAD EN EL CONTEXTO DE LAS VARIEDADES BANÁSICAS CON BORDE ANGULOSO LEMA (1. 2. 10 de [M. O. ])

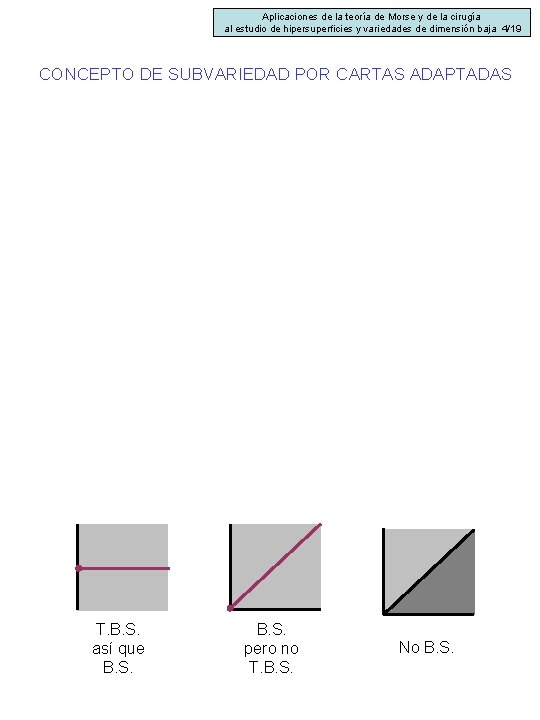
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 4/19 CONCEPTO DE SUBVARIEDAD POR CARTAS ADAPTADAS T. B. S. así que B. S. pero no T. B. S. No B. S.

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 5/19 OBJECIONES A LA DEFINICIÓN - EL PROBLEMA DE LA TRANSITIVIDAD: - EL PROBLEMA DE LA BUENA INMERSIÓN: Sumergir en cuadrantes de Espacios de Banach como subvariedad bien situada. - EL PROBLEMA DE LA TRANSVERSALIDAD: Z ½ Y subvariedad. f : X ! Y transversal a Z. Pero f-1(Z) no es, en general, subvariedad de X. - LA INTERSECCIÓN DE SUBVARIEDADES TRANSVERSALES NO SIEMPRE ES UNA SUBVARIEDAD. - EL PROBLEMA DE LA GRÁFICA: Para asegurar que la gráfica de f : X ! Y diferenciable sea subvariedad de X £ Y es necesario exigir Y = ; .

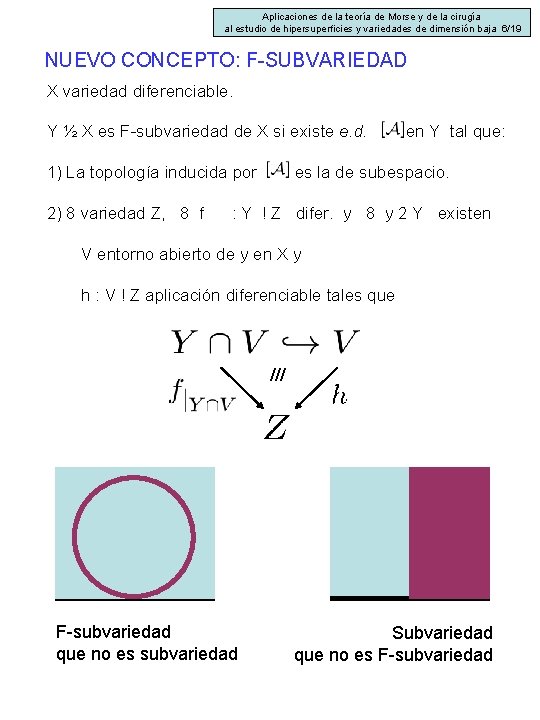
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 6/19 NUEVO CONCEPTO: F-SUBVARIEDAD X variedad diferenciable. Y ½ X es F-subvariedad de X si existe e. d. 1) La topología inducida por 2) 8 variedad Z, 8 f en Y tal que: es la de subespacio. : Y ! Z difer. y 8 y 2 Y existen V entorno abierto de y en X y h : V ! Z aplicación diferenciable tales que /// F-subvariedad que no es subvariedad Subvariedad que no es F-subvariedad

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 7/19 VENTAJAS-NATURALIDAD DE LA NUEVA DEFINICIÓN - NO REQUIERE CARTAS: Produce enunciados de sencilla formulación. - ES EL CONCEPTO DUAL DE SUMERSIÓN: Una F-inmersión es localmente la sección de una sumersión. - NOCIÓN DOTADA DE SENTIDO FÍSICO: es exacta. - SE HAN OBTENIDO LOS RESULTADOS ESPERADOS Y CON LA ANTIGUA DEFINICIÓN NO CONSEGUIDOS: Se resuelven positivamente los problemas de transitividad, transversalidad e intersección de subvariedades transversales, gráfica de la función e inmersión bien situada.

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 8/19 LA CARENCIA DE CARTAS ADAPTADAS CONDUCE A PRUEBAS ‘DISTINTAS’ Teorema 1. 9 f : X ! Y diferenciable y x 2 X. Suponemos: 1) f preserva el borde localmente en x. 2) f preserva el índice de los vectores interiores en x. Entonces f es inmersión en x si y sólo si f es F-inmersión en x. Teorema 2. 17 Sub. T. B. S. , F-sub. T. B. S. Teorema 2. 18 Sub. B. S. ) F-sub. Teorema 2. 23 Localmente toda F-subvariedad es a la vez subvariedad y F-subvariedad si agrandamos la variedad ambiente adecuadamente. Teorema 4. 7 La imagen inversa de una F-subvariedad por una aplicación transversal a ésta es siempre una F-subvariedad. Ejemplo 3. 3 La imagen inversa de una F-subvariedad por una aplicación que es sumersión en todo punto de la imagen inversa no es necesariamente una F-subvariedad.

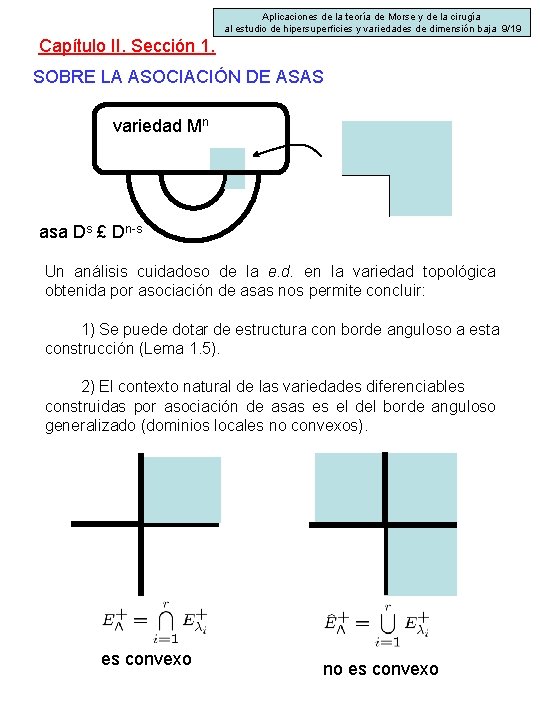
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 9/19 Capítulo II. Sección 1. SOBRE LA ASOCIACIÓN DE ASAS variedad Mn asa Ds £ Dn-s Un análisis cuidadoso de la e. d. en la variedad topológica obtenida por asociación de asas nos permite concluir: 1) Se puede dotar de estructura con borde anguloso a esta construcción (Lema 1. 5). 2) El contexto natural de las variedades diferenciables construidas por asociación de asas es el del borde anguloso generalizado (dominios locales no convexos). es convexo no es convexo

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 10/19 Capítulo II. Sección 2. ASAS Y 4 -ESFERAS EXÓTICAS Teorema 2. 1 Si M es una esfera exótica de dimensión cuatro, existe un número natural k tal que M se obtiene de la suma conexa de k copias de S 2 £ S 2 mediante k cirugías de tipo (3, 2).

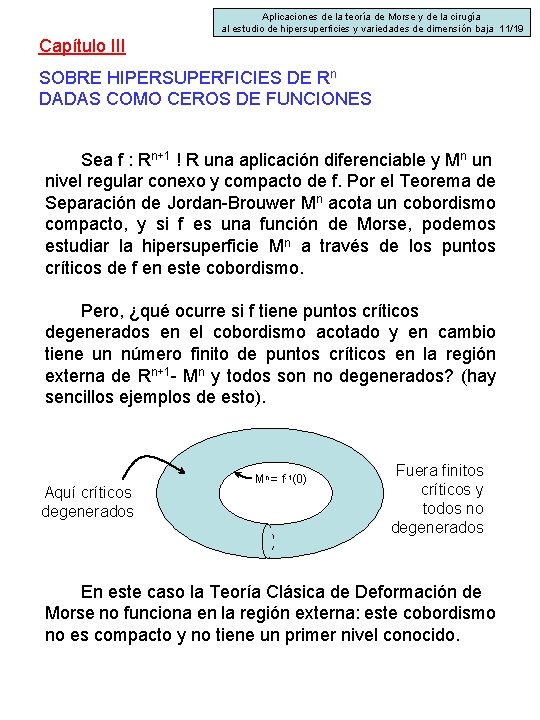
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 11/19 Capítulo III SOBRE HIPERSUPERFICIES DE Rn DADAS COMO CEROS DE FUNCIONES Sea f : Rn+1 ! R una aplicación diferenciable y Mn un nivel regular conexo y compacto de f. Por el Teorema de Separación de Jordan-Brouwer Mn acota un cobordismo compacto, y si f es una función de Morse, podemos estudiar la hipersuperficie Mn a través de los puntos críticos de f en este cobordismo. Pero, ¿qué ocurre si f tiene puntos críticos degenerados en el cobordismo acotado y en cambio tiene un número finito de puntos críticos en la región externa de Rn+1 - Mn y todos son no degenerados? (hay sencillos ejemplos de esto). Aquí críticos degenerados Mn = f-1(0) Fuera finitos críticos y todos no degenerados En este caso la Teoría Clásica de Deformación de Morse no funciona en la región externa: este cobordismo no es compacto y no tiene un primer nivel conocido.

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 12/19 Proposición 1. 12 (Aplicaciones Propias) f : Rn+1 ! R continua de fibras compactas y no acotada superiormente (n 2 N). Entonces f es propia. Teorema 1. 13 Para toda Mn hipersuperficie compacta de Rn+1 existe f: Rn+1 ! R de clase infinita, propia y de Morse con C(f) finito, Mn = f-1(0) y 0 valor regular de f. Teorema 2. 1 Mn = f -1(0) hipersuperficie compacta y conexa de Rn+1. f : Rn+1 ! R de Morse con 0 valor regular de f. Suponemos f de fibras compactas o Palais-Smale. Entonces, si f no tiene puntos críticos en la componente conexa no acotada de Rn+1 - Mn, se verifica que: i) Mn es una 3 -esfera de homotopía si n = 3. ii) Mn es homeomorfa a S 4 si n = 4. iii) Mn es difeomorfa a Sn si n ¸ 5 ó n = 2. Lema 2. 4 (Conexión de fibras) f : Rn+1 ! R diferenciable de fibras compactas (n 2 N). 2 R valor regular de f y cota superior de f(C(f)). Entonces f-1( ) es conexo (tal vez vacío).

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 13/19 Lema 2. 4 ) + Teorema 2. 1 INFORMACIÓN DE LA HIPERSUPERFICIE A PARTIOR DE LOS PUNTOS CRÍTICOS EN LA REGIÓN EXTERIOR Corolario 2. 5 S superficie conexa de R 3 nivel regular de una función f: R 3 ! R propia. Entonces, si f tiene un único punto crítico “afuera” y es no degenerado, S es un toro. Ejemplo 2. 6 Sea g : R 3 ! R la aplicación polinómica dada por Entonces g-1(0) es un toro. Corolario 2. 8 Mn hipersuperficie compacta conexa de Rn+1 con n ¸ 5. Entonces Mn Sn si y sólo si existe f : Rn+1 ! R C 1 de fibras compactas, Mn = f-1(0), 0 es valor regular de f y f no tiene puntos críticos en la región no acotada.

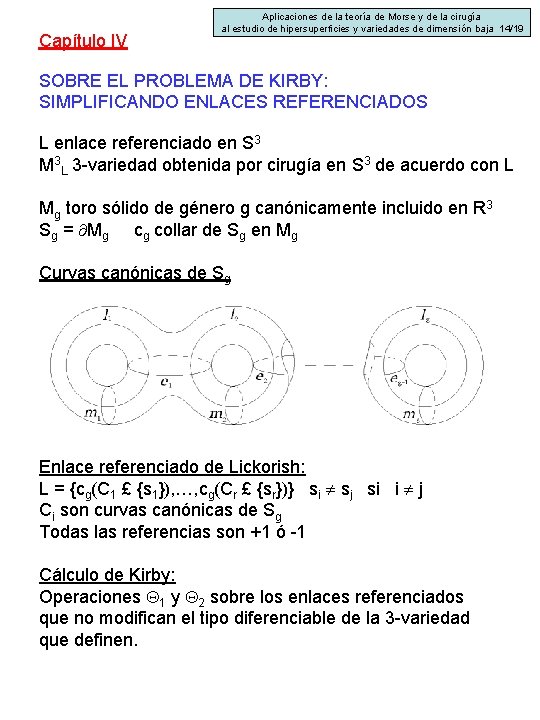
Capítulo IV Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 14/19 SOBRE EL PROBLEMA DE KIRBY: SIMPLIFICANDO ENLACES REFERENCIADOS L enlace referenciado en S 3 M 3 L 3 -variedad obtenida por cirugía en S 3 de acuerdo con L Mg toro sólido de género g canónicamente incluido en R 3 Sg = Mg cg collar de Sg en Mg Curvas canónicas de Sg Enlace referenciado de Lickorish: L = {cg(C 1 £ {s 1}), …, cg(Cr £ {sr})} si sj si i j Ci son curvas canónicas de Sg Todas las referencias son +1 ó -1 Cálculo de Kirby: Operaciones 1 y 2 sobre los enlaces referenciados que no modifican el tipo diferenciable de la 3 -variedad que definen.

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 15/19 Teorema Fundamental de la Cirugía en 3 -variedades (R. W. B. Lickorish, 1960 -1962 -1964) Toda 3 -variedad es M 3 L para algún enlace referenciado L de Lickorish. Teorema del Cálculo (R. C. Kirby, 1978) ML 3 ¼ M 3 L’ si y sólo si L’ se obtiene de L mediante las operaciones 1 y 2. PLANTEAMIENTO DEL PROBLEMA (Kirby, 1978 -1990) - ¿Qué debemos entender por enlace “canónico” o “minimal” para una 3 -variedad? - Construir un algoritmo para pasar de un enlace referenciado arbitrario a uno canónico que defina la misma 3 -variedad.

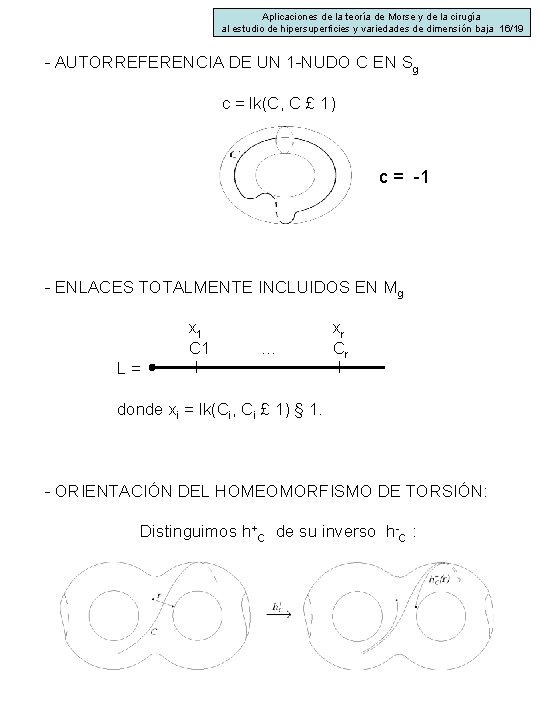
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 16/19 - AUTORREFERENCIA DE UN 1 -NUDO C EN Sg c = lk(C, C £ 1) c = -1 - ENLACES TOTALMENTE INCLUIDOS EN Mg x 1 C 1 … L= xr Cr donde xi = lk(Ci, Ci £ 1) § 1. - ORIENTACIÓN DEL HOMEOMORFISMO DE TORSIÓN: Distinguimos h+C de su inverso h-C :

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 17/19 EL CONCEPTO DE AUTORREFERENCIA EN EL TEOREMA DE LICKORISH Lema 2. 12 Sean B un 1 -nudo en Sg, un signo, y e : A = { rei 2 C / 1 · r · 2, 2 R } ! Sg una inmersión topológica preservando la orientación con e(S 13/2) = B. Sea W = cg(im(e) £ [n, n+1]) para cierto n 2 N. Entonces W es un toro sólido incluido en Int Mg, la aplicación : M g - Int. W ! Mg – Int. W definida por está bien definida, es homeomorfismo, ( W) = W y |Sg = h B. Además si ( ) es el meridiano de W, entonces es una longitud de W tal que lk( , W) = lk(B, B £ 1) + donde W = cg(B £ {n + 1/2}) es el ánima de W.

Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 18/19 Corolario 2. 13 C 1, … , Cr 1 -nudos en Sg. 1, …, r signos. Entonces Mg [ h Mg ¼ ML 3 donde y L es el enlace referenciado totalmente incluido en Mg L= 1 1 m 1 l 1 … 1 1 mg lg c 1 - 1 cr - r C 1 … Cr siendo c i = lk(C i, C i £ 1) la autorreferencia de cada Ci. Ejemplo 2. 14 Los siguientes enlaces referenciados definen la misma 3 -variedad: Corolario 2. 15 Existe un algoritmo que transforma en enlace de Lickorish cualquier enlace totalmente incluido en Mg.

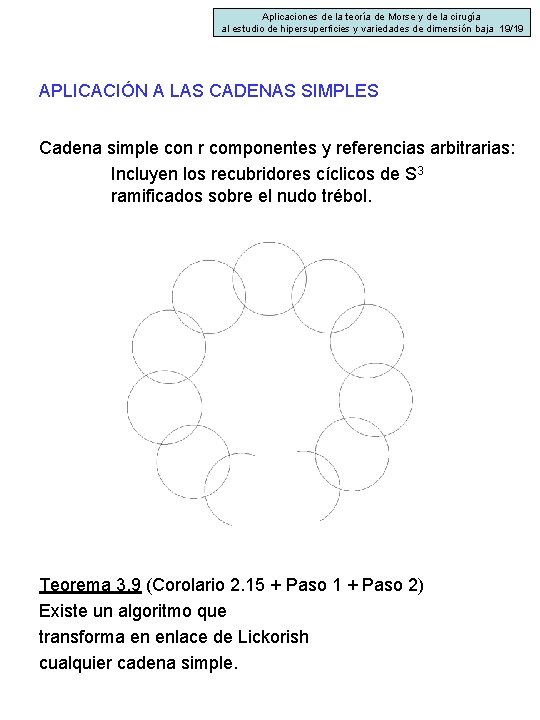
Aplicaciones de la teoría de Morse y de la cirugía al estudio de hipersuperficies y variedades de dimensión baja 19/19 APLICACIÓN A LAS CADENAS SIMPLES Cadena simple con r componentes y referencias arbitrarias: Incluyen los recubridores cíclicos de S 3 ramificados sobre el nudo trébol. Teorema 3. 9 (Corolario 2. 15 + Paso 1 + Paso 2) Existe un algoritmo que transforma en enlace de Lickorish cualquier cadena simple.