Dealing with Nuisances Principled and Ad Hoc Methods

Dealing with Nuisances: Principled and Ad Hoc Methods Xiao-Li Meng Department of Statistics, Harvard University Joint work with Jingchen Liu (and CHASC) 9/25/2021 Harvard University 1

Dealing with Nuisance Parameters Bringing in a little “Bee”: Posterior Predictive Assessment n Giving up a bit of power: Using an alternative (or a “working” alternative) n Being further away from the big “Bee”: Profiling via moments n 9/25/2021 Harvard University 2

A Simple Spectral Model n n A source spectrum with two components: a continuum modeled by a power law E- , and an emission line modeled as a Gaussian profile with a total flux F. The expected observed flux Fj from the source within an energy bin Ej for a “perfect” instrument is given by n where d. Ej is the energy width of bin j, and j is the Gaussian proportion in bin j. If the exact energy is observed, then the distribution follows n Reference: Protassov et al (2002) 9/25/2021 Harvard University 3

Hypothesis Testing – Notation n n n Likelihood L( |x) = f(x| ), = 0[ 1, 0 1=; Null Hypothesis H 0: 2 0 Alternative Hypothesis HA: 2 1 Critical region: C ) Reject null hypothesis if x 2 C. Type I error: P(X 2 C | 2 0) – False negative rate Type II error: P(X 2 Cc | 2 A) – False positive rate Power function: p( ) = P(X 2 C | ) Hypothesis testing of size : p( ) · , 8 2 0 9/25/2021 Harvard University 4

Hypothesis Testing – Likelihood Ratio Test n n n Uniformly most powerful (UPM) test: the most powerful test among all the tests with size Likelihood ratio test (LRT): C(c) = {x : LR(x) > c} In a simple null hypothesis case, if the UMP test exists, it is likelihood ratio test. 9/25/2021 Harvard University 5

Seeking Pivotal Quantity n n Hypothesis testing of size : max 2 P(X 2 C | ) = , hard 0 to maximize. Ideally, we seek a pivotal quantity: T(X) -- its distribution is completely known under the null 0 Then type I error P(T(X)>t| ) = , 8 2 0, Easy to control type I error, but typically it is very hard to find a useful/powerful pivotal quantity. 9/25/2021 Harvard University 6

Posterior Predictive Assessment n n n n p-value = P(T(X) > T(x)| 0), In the presence of nuisance parameter , under the null, the p-value will be a function of , p( ) = P(T(X) > T(x) | ). Posterior predictive p-value: ppp=E(p( ) | x) = s p( ) f( | x) d , where f( | x) is the posterior density of . That is, the p-value is calculated under the posterior predictive distribution: f(Xrep|x) = s f(Xrep| 0, ) f( | x) d Casting doubt on the null hypothesis/model if a ppp is extreme. Can use realized discrepancy D(X, ): p( ) = P(D(X , ) > D(x, ) | ). Can assess the entire posterior distribution of p( ). References: Rubin (1984), Meng (1994), Gelman, Meng and Stern (1996) 9/25/2021 Harvard University 7

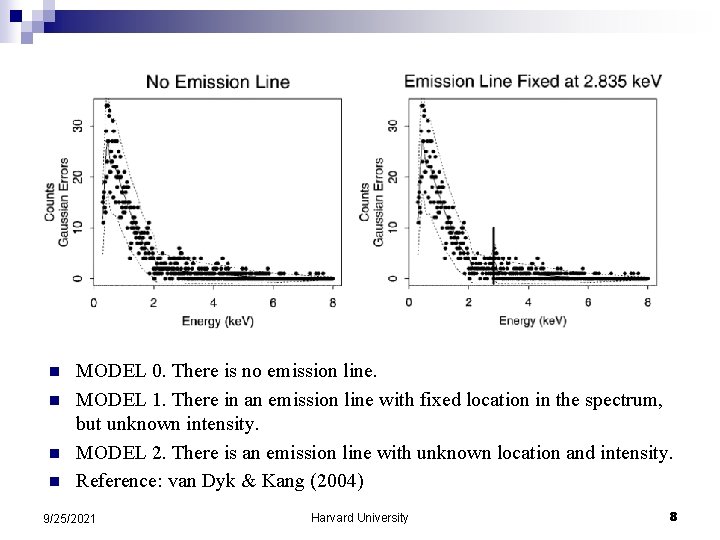
n n MODEL 0. There is no emission line. MODEL 1. There in an emission line with fixed location in the spectrum, but unknown intensity. MODEL 2. There is an emission line with unknown location and intensity. Reference: van Dyk & Kang (2004) 9/25/2021 Harvard University 8

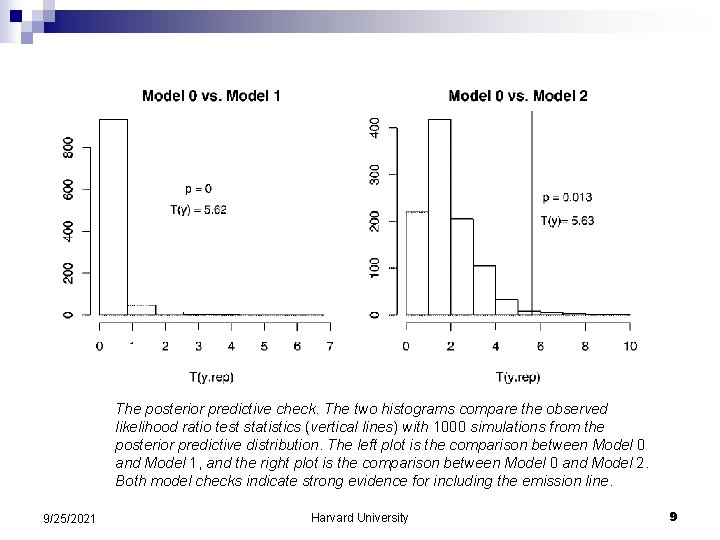
The posterior predictive check. The two histograms compare the observed likelihood ratio test statistics (vertical lines) with 1000 simulations from the posterior predictive distribution. The left plot is the comparison between Model 0 and Model 1, and the right plot is the comparison between Model 0 and Model 2. Both model checks indicate strong evidence for including the emission line. 9/25/2021 Harvard University 9

Mixture Model - Testing p = 0 n Hypothesis testing of mixture model n Particularly, f(x | ) / x- , g(x | , ) = (x| , ) n n (To avoid singularity at the 0, when > 1, we need to truncate the density away from 0. Without losing generality, we assume x > 1. ) LR is not a pivotal quantity under this model. But if we use a different model for the g component, then we can construct a LR test that is a pivotal quantity. Let y = log (x) and = 1 / ( - 1), then we can model 9/25/2021 Harvard University 10

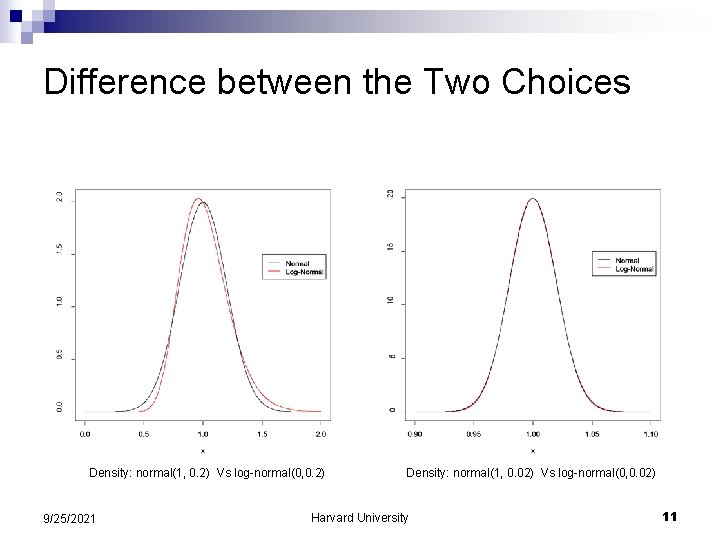
Difference between the Two Choices Density: normal(1, 0. 2) Vs log-normal(0, 0. 2) 9/25/2021 Density: normal(1, 0. 02) Vs log-normal(0, 0. 02) Harvard University 11

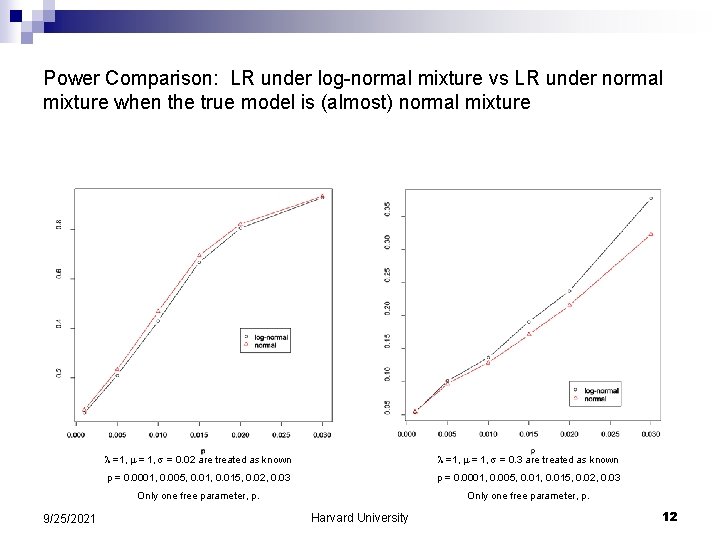
Power Comparison: LR under log-normal mixture vs LR under normal mixture when the true model is (almost) normal mixture 9/25/2021 =1, = 0. 02 are treated as known =1, = 0. 3 are treated as known p = 0. 0001, 0. 005, 0. 01, 0. 015, 0. 02, 0. 03 Only one free parameter, p. Harvard University 12

Likelihood Ratio Test and Pivotal Quantity n n H 0: p = 0, HA: p > 0 The LRT is pivotal quantity, i. e. , the distribution of likelihood ratio is free of . The maximization can be done via the EM algorithm by viewing the subgroup membership as missing data. 9/25/2021 Harvard University 13

Expectation-Maximization Algorithm

Multiple Modes log Likelihood of given that = 1, = 0. 02, p = 0. 01, the sample size is 500 9/25/2021 Harvard University 15

A “Profiled” Likelihood Ratio Test n “Profile likelihood” via moment n Lp( p, , | y) can be maximized via numerical optimization method (the correct likelihood was harder to maximize without using EM). Let’s define critical region C( c ) = {y | LRp(y) > c} n 9/25/2021 Harvard University 16

A Sketch of Proof 9/25/2021 Harvard University 17

Demonstrating a pivot: QQ-plot of LRs when = 1 vs = 10 Profile Likelihood 9/25/2021 EM Harvard University 18

Distribution of 2 log (LR )’s under the null hypothesis Profile Likelihood 9/25/2021 EM: Starting from E( | y)= 0. 5 Harvard University 19

Power Comparison: “Profile” LRT vs “EM” LRT 9/25/2021 Harvard University 20

References n n n Gelman, A. , Meng, X. L. , and Stern, H. (1996). Posterior predictive assessment of model fitness via realized discrepancies (with discussions). Statistica Sinica, 6, 733 -807 Meng, X. L. (1994). Posterior predictive p-values. Ann. Stat. 22: 1142 1160. Protassov, R. , van Dyk, D. A. , Connors, A. , Kashyap, V. L. , and Siemiginowska, A. (2002) Statistics: Handle with Care, Detecting Multiple Model Components with the Likelihood Ratio Test. The Astrophysical Journal, 571: 545– 559 Rubin, DB (1984). Bayesianly justifiable and relevant frequency calculations for the applied statistician. Annals of Statistics, 12(4), 1151– 1172 van Dyk, D. A. , and Kang, H. (2004). Highly Structured Models for Spectral Analysis in High-Energy Astrophysics. Statistical Science, 9, no. 2, 275– 293 9/25/2021 Harvard University 21

Topic “B” reinstated: How to measure “ego”? n How to classify professions by such “ego” measures? n Finding the most powerful test for testing n Ego_Particle Physicists > Ego_Astrophysicists> Ego_Statisticians 9/25/2021 Harvard University 22