D E ZEGOUR Ecole Suprieure dInformatique INTRODUCTION LA

D. E ZEGOUR Ecole Supérieure d’Informatique INTRODUCTION À LA THÉORIE DE LA COMPLEXITÉ

Théorie de la complexité Introduction générale Comment une solution est complexe, difficile ? Plusieurs manières de mesurer la complexité d’une solution : Facile / difficile à l’ exprimer Facile / difficile à traiter (exécuter) en temps /espace Autres mesures importantes : Energie, Communications L’étude de la complexité a pour but de quantifier ses mesures.

Théorie de la complexité Introduction générale L’étude de la complexité a débuté avec l’invention des ordinateurs commerciaux (1950 à 1960) - processeurs étaient lents et les mémoires beaucoup plus chères qu’aujourd’hui - il était très important de concevoir des algorithmes efficaces. De nos jours, reste un problème d’actualité et très ouvert. Discipline très importante.

Théorie de la complexité Introduction générale Point de départ : formalisation du concept d’algorithme. Complexité étudié a travers un modèle de calcul. Machine de Turing (cependant, il existe d’autres modèles) Ces machines correspondent à la classification des grammaires (langages ) selon Chomsky, (Ex : Machine Turing (Type 0) , langages de programmation (type 2) , … ) Domaine en informatique : conception et analyse des algorithmes (proposé par Knuth)

Théorie de la complexité Introduction générale Problèmes centraux étudiés dans la théorie de la complexité : • Pour une quantité de ressources donnée ou pour un type de ressource, quels sont les problèmes qu’on peut résoudre et ceux qu’on ne peut pas résoudre? • Quelle est la relation entre les problèmes exigeant essentiellement la même quantité de ressource ? sont t-ils équivalents dans un certain sens? • Quelle est le lien entre les différents type de ressources ? Avec plus de temps consommé, peut-on réduire l’espace ou vice versa ?

Théorie de la complexité Introduction générale La dernière force du fameux papier de Turing était de démontrer rigoureusement que plusieurs problèmes fondamentaux de la logique ne peuvent pas être résolu par des algorithmes La théorie de la complexité vise à montrer des résultats similaires pour beaucoup d’autres problèmes quand les ressources sont limitées. De tels problèmes insolubles bien que "mauvaises nouvelles" dans plusieurs domaines peuvent avoir des bénéfices pratiques. Dans ce cas les heuristiques sont utilisées.

Théorie de la complexité Problèmes solubles / Problèmes non solubles Il ya des problèmes pour lesquels on connait des réponses. - Etant donné un polynôme P quelconque, ayant un nombre quelconque de variables, est-ce que P admet des racines entières ? (Dixième problème de Hilbert) La réponse est NON. - Etant donné une formule F quelconque de la logique propositionnelle, estce que F est satisfiable (Il existe une combinaison de valeurs pour les variables propositionnelles de F pour laquelle F est vraie) ? La réponse est OUI. - Même question que ci-dessus, mais avec les formules de la logique du premier ordre. La réponse est NON.

Théorie de la complexité Problèmes solubles / Problèmes non solubles Il ya des problèmes pour lesquels on ne connait pas de réponses. Problème de Fermat ( il ya 3 siècles) reste toujours d’actualité En entrée : n En sortie les triplets (x, y, z) entiers tels que xn + yn = zn Si n=2, on a une solution x= 3, y= 4 , et z=5 Si n>2, on ne sait pas s’il ya des solutions entières.

Théorie de la complexité Problème de Fermat comme un programme

Théorie de la complexité Problèmes solubles / Problèmes non solubles Il ya des problèmes pour lesquels on ne connait pas de réponses. Fameux problème : version arithmétique de SAT. Etant donné une équation polynomiale à plusieurs variables, comme x 3 yz + 2 y 4 z 2 - 7 xy 5 z = 6; Existe-il des valeurs pour x, y et z qui rendent l’équation satisfaite ? Il n y a pas d’algorithme qui résout ce problème ( ni polynomial, ni exponentiel, ou pire ) Le premier problème insoluble (LEQUEL? )a été découvert en 1936 par Alan M. Turing, alors qu’il était étudiant de Mathématique ( il n’ y avait ni ordinateur ni langage de programmation!)

Théorie de la complexité Problèmes traitables / Problèmes non traitables Parmi les problèmes solubles - Quels sont les problèmes qu'un ordinateur peut traiter ? - Quels sont les problèmes qu'un ordinateur ne peut pas traiter ? Dans le cas de problèmes traitables : - Est ce que le temps (espace) pris par l'exécution est acceptable ? - Est-ce que les méthodes approchées peuvent être utilisées ? Les machines ont des limites théoriques : elles ne peuvent pas résoudre TOUS les problèmes. Néanmoins, elles en résolvent un grand nombre !

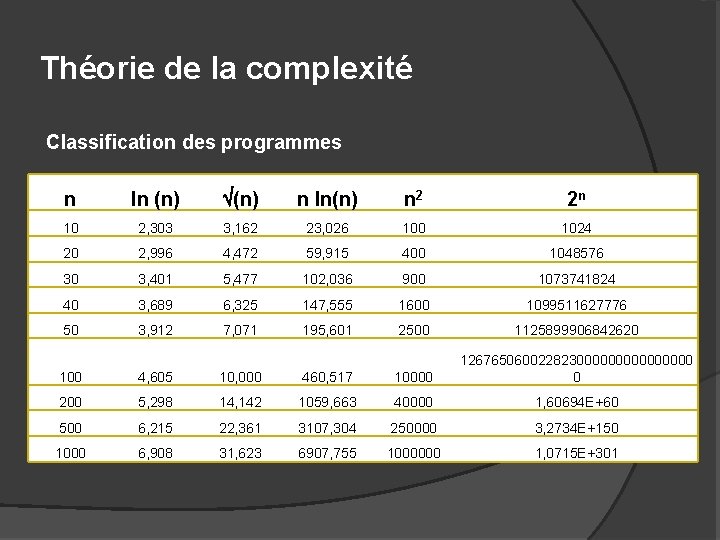
Théorie de la complexité Classification des programmes O(1): Temps d’exécution indépendant de la taille du problème n. O(ln(n)): un grand problème est résolu par sa décomposition en sous problème de taille plus petite. (Logarithmique) O(n): chaque élément du problème n exige un petit traitement (Linéaire) O(n × ln(n)): Un problème est divisé en petits sous problèmes. On résout chaque sous problème à part et on combine les solutions(Linéaire logarithmique) O(n 2): le problème nécessite le traitement de toutes les paires d’éléments. (Quadratique) O(2 n): Temps exponentiel. A éviter. Caractéristiques des méthodes “Essayer toutes les possibilités". (Exponentielle).

Théorie de la complexité Classification des programmes n ln (n) n ln(n) n 2 2 n 10 2, 303 3, 162 23, 026 100 1024 20 2, 996 4, 472 59, 915 400 1048576 30 3, 401 5, 477 102, 036 900 1073741824 40 3, 689 6, 325 147, 555 1600 1099511627776 50 3, 912 7, 071 195, 601 2500 1125899906842620 100 4, 605 10, 000 460, 517 10000 12676506002282300000000 0 200 5, 298 14, 142 1059, 663 40000 1, 60694 E+60 500 6, 215 22, 361 3107, 304 250000 3, 2734 E+150 1000 6, 908 31, 623 6907, 755 1000000 1, 0715 E+301

Théorie de la complexité Classification des programmes ( si chaque étape prend 10 -3 ms ) ln (n) n ln(n) n 2 2 n 0, 1 s 4, 605 ms 10 ms 0, 46 s 10 s 40196936841331500000 siècles 0, 2 s 5, 298 ms 14, 142 ms 1, 059 s 40 s 5, 09557 E+47 siècles n 10 20 30 40 50 500 1000

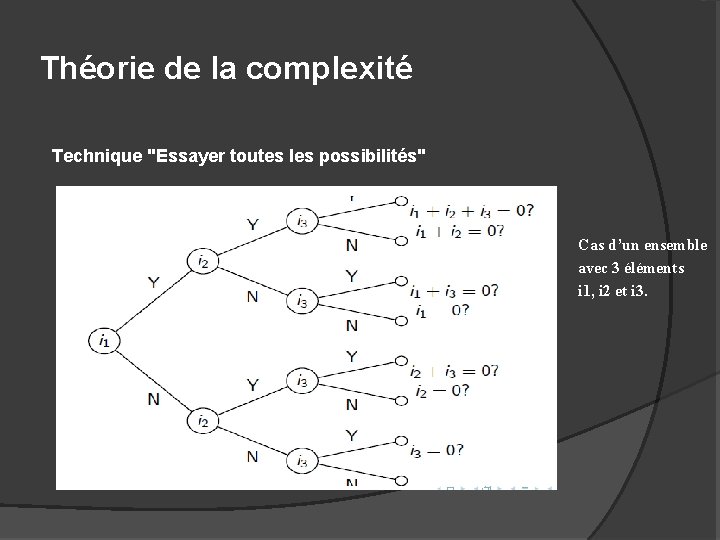
Théorie de la complexité Technique "Essayer toutes les possibilités" Exemple 1: (The subset-sum problem (SSP)) Etant donné un ensemble d’entiers S = {i 1, i 2, . . . , in}, est-ce qu’il existe un sous ensemble A de S tel que la somme de ses éléments est égale à 0? Exemple, y a t-il un sous enemble de {− 2, − 3, 15, 14, 7, − 10} avec une somme égale à 0? Réponse : OUI car “{− 2, − 3, − 10, 15} est un candidat ( facile à vérifier) Si on vous demande de trouver, ce n’est pas évident

Théorie de la complexité Technique "Essayer toutes les possibilités" Cas d’un ensemble avec 3 éléments i 1, i 2 et i 3.

Théorie de la complexité Technique "Essayer toutes les possibilités" Si S = {i 1, i 2, . . . , in} Complexité: - Pour chaque entier, il ya deux choix. Comme il ya n entiers, il ya 2 n branches. Pour chaque branche, on fait au plus n additions, Donc la complexité est O(n × 2 n).

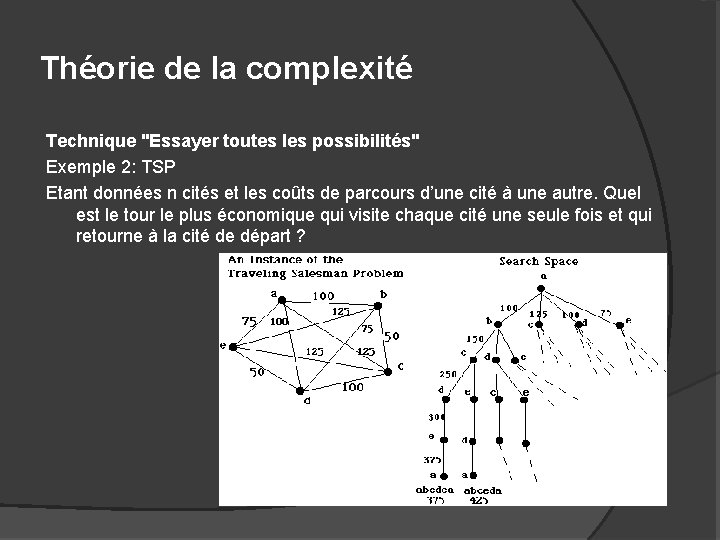
Théorie de la complexité Technique "Essayer toutes les possibilités" Exemple 2: TSP Etant données n cités et les coûts de parcours d’une cité à une autre. Quel est le tour le plus économique qui visite chaque cité une seule fois et qui retourne à la cité de départ ?

Théorie de la complexité Technique "Essayer toutes les possibilités" Complexité: Une branche = une séquence de n cités. Nombre de branches différentes? A chaque étape k on peut choisir parmi n − k cités. Donc le nombre de branches est = (n − 1) × (n − 2) · · · × 1 = (n − 1)!. Complexité : O((n − 1)!). Algorithme (hyper-)exponential n! = O((n/2)n))

Théorie de la complexité Modèle de calcul et complexité L’étude de la calculabilité (décidabilité) nécessite l’utilisation d’un modèle théorique qui soit indépendant du langage et de l’ordinateur Exemple de modèle : machine de Turing caractérise tout ce qui est calculable Mathématicien anglais Alan Turing (machine conçue en 1936) (Turing est aussi célèbre pour avoir décodé les messages des nazis pendant la seconde guerre mondiale, et pour avoir inspiré le logo de la firme Apple). Autres modèles : Lambda calcul, Machines à registres, Circuit logique, Fonctions récursives, etc.

Théorie de la complexité Principe de Church-Turing "Tout ce qui peut être calculé, peut l’être par une machine de Turing" Simple affirmation (jamais mise en défaut) Tout ce qui peut être calculé = ce qui peut être obtenu par une machine (au sens large) en un temps fini.