CSC 778 Optical Networking Rudra Dutta Fall 2007

CSC 778 - Optical Networking Rudra Dutta, Fall 2007 NP-Completeness, Optimization, in Network Design Copyright Rudra Dutta, NCSU, Fall, 2007

Complexity and Optimization l Most “problems” are NOT “solvable” Others are merely hard to solve – This includes many practically interesting problems – l Sometimes solutions are not just costly, but. . . – l Optimization techniques allow modeling such problems – l Difficult or impossible to express Sometimes provide “good” if not “perfect” solutions Bottom-line: part of the language of complex network design, must understand Copyright Rudra Dutta, NCSU, Fall, 2007 2

Complexity Theory, NP-Completeness Copyright Rudra Dutta, NCSU, Fall, 2007

Algorithms Information representation by bits l Algorithms as manipulators of bits l Abstract manipulations of abstract data types l – Not specific to machine architecture etc. Copyright Rudra Dutta, NCSU, Fall, 2007 4

Asymptotic Complexity l Complexity - number of elemental steps required What is a step? – Worst case, average case? – Naturally, problem instances of bigger “size” can reasonably take more steps l Asymptotic - beyond a certain “size” f, g: N N f is O(g) iff N, c: f(n) c g(n) n N g is (f) f is (g) iff f is O(g) and (g) l Copyright Rudra Dutta, NCSU, Fall, 2007 5

Languages Alphabet - a finite set of symbols (S) l String - finite ordered list of symbols from S l – l The empty string is denoted by e Universe of strings S* – All strings of length k - Sk Concatenation, suffix, prefix, substring l Language - a subset of S* l Characteristic function c. L l Examples on S = {0, 1} l L = {00, 01, 10, 11} = S 2 – L = {x ends with a single 0 after one or more 1’s} – Copyright Rudra Dutta, NCSU, Fall, 2007 6

Infinite Sets and Computability Function, domain, co-domain, range l Surjective (onto) l – l Range = co-domain Injective (one-to-one) – Distinct elements mapped to distinct elements Bijective: both l Bijection allows comparison of infinite set sizes l |N| = |E| = |O| = 0 , countable infinity – Q = N x N, 0. 0 = 0 – Diagonalization argument : R is not countable – 2 N is not countable - most functions not computable – Copyright Rudra Dutta, NCSU, Fall, 2007 7

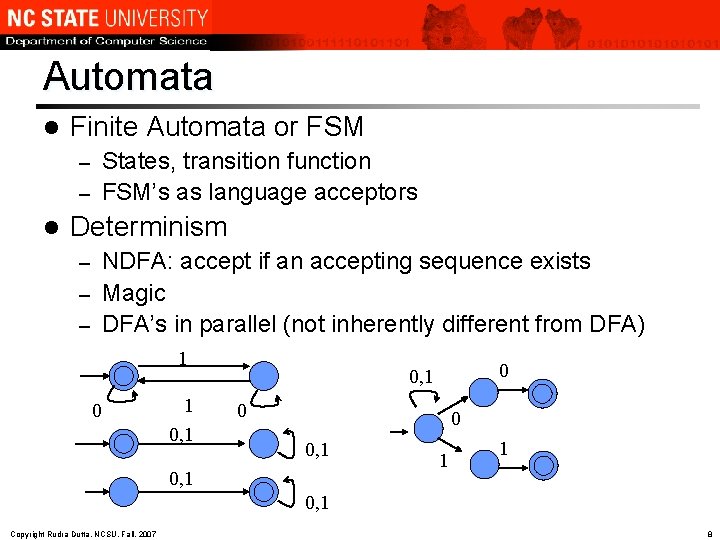
Automata l Finite Automata or FSM States, transition function – FSM’s as language acceptors – l Determinism NDFA: accept if an accepting sequence exists – Magic – DFA’s in parallel (not inherently different from DFA) – 1 0, 1 0 0 0, 1 1 1 0, 1 Copyright Rudra Dutta, NCSU, Fall, 2007 8

Computational Models l A language (or function) is a problem – l Regular expressions and regular languages – l Program computes desirable quantity for each instance of a problem - decision or optimization Shown to be equivalent to finite automata The Halting Problem A diagonalization argument on programs – Assume such a program exists – Make another which stops only if it returns “yes” – l Universal models of computation – Several now known, (polynomial) equivalent Copyright Rudra Dutta, NCSU, Fall, 2007 9

Turing Machines l Turing machine is quite convenient Concept of “steps” and “space” are obvious – Difference in scale with practical computers – l Reads problem on tape, ends with solution Non-determinism does not increase power – Multiple tapes do not increase power – l Acceptors and enumerators Finite-state control Copyright Rudra Dutta, NCSU, Fall, 2007 10

Computability l Primitive Recursive functions Zero, Succ, Pick – Build other functions by: – Substitution l Primitive recursion: f(0) = x, f(i + 1) = h(i, f(i)) l l PR functions are computable, but computable functions that are not PR exist – l Diagonalization Partial Recursive functions Not defined for all input - avoid diagonalization – µ-recursion or minimization: find minimum (extra) argument that makes another function return zero – Copyright Rudra Dutta, NCSU, Fall, 2007 11

Function Classes All partial functions total partial recursive not total primitive recursive Copyright Rudra Dutta, NCSU, Fall, 2007 12

Further on Computability Recursive and R. E. sets l Rice’s Theorem l Reductions, classes of reduction l Hardness, easiness, completeness l Copyright Rudra Dutta, NCSU, Fall, 2007 13

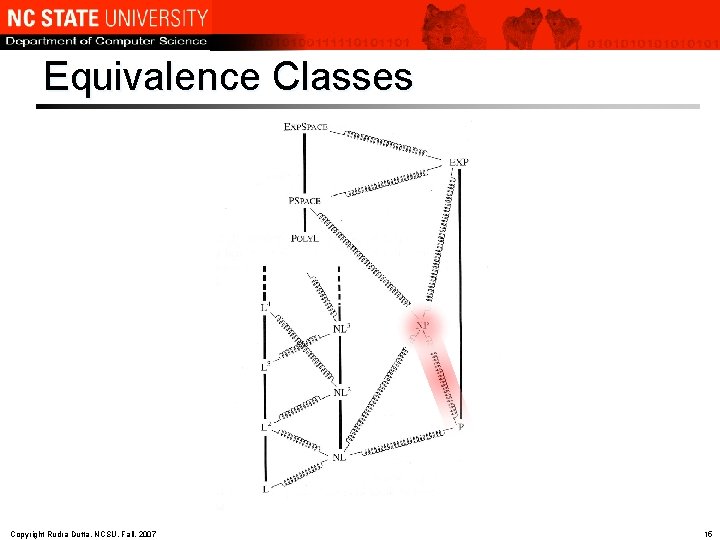
Classes and Reductions Some problems are equivalent to others l Others are “at least as difficult as” l Concept of reduction l – l More explanatory names: “equivalence” or “transformability” Different kinds of reduction Generic versus specific – Turing versus many-to-one – l Reductions allow equivalence classes to be built – But finding first complete problem (generic) could be difficult Copyright Rudra Dutta, NCSU, Fall, 2007 14

Equivalence Classes Copyright Rudra Dutta, NCSU, Fall, 2007 15

Cook’s Theorem l Satisfiability is NP-Complete A collection of Boolean clauses – Problem: Decide whether truth assignment satisfying all the clauses exists – l Given an instance of a decision problem in NP, an instance of Satisfiability can be produced in polynomial time, which is satisfiable iff the original instance is a “yes” instance Copyright Rudra Dutta, NCSU, Fall, 2007 16

Many-to-One Reductions First show problem at hand is in NP l Pick a known NPC problem to reduce from l All instances of the problem must be amenable to reduction – If not, danger of picking tractable subset – l Define a function to transform instance into instance of target Must be polynomial procedure – Need not reach all instances of target – Hence many-to-one, not one-to-one or onto – l Special case: restriction – Of problem space, not solution method Copyright Rudra Dutta, NCSU, Fall, 2007 17

Decision and Optimization Most problems can be stated in either of two versions l Generally interchangable l Proof of computational complexity class with one is often taken as proof for another – Complexity proofs attempted for decision versions – l Decision - quantified yes-no question – l “Can you finish your shopping within x dollars? ” Optimization - best-of-class question – “How few dollars can you finish your shopping within? ” Copyright Rudra Dutta, NCSU, Fall, 2007 18

Well Known NPC Problems l Three-satisfiability Each clause has exactly three literals – 1 in 3 Sat – NAE 3 Sat – l l l Max. Cut Partition Exact Cover by 3 -sets Chromatic number Knapsack Bin-packing Copyright Rudra Dutta, NCSU, Fall, 2007 19

An Example Knapsack: Given a set of elements, a positive integer size and value for each, a positive integer size upper bound and value lower bound, does a subset meeting the bounds exist? l Partition: Given a set of elements, each with a positive integer size such that the sum of all sizes is an even number, can the set by partitioned into two subsets such that the sum of elements in each subset is equal? l Restriction: In Knapsack, allow only instances where the sum of all sizes is a multiple of 2, size equals value for each element, and bounds are each equal to half the sum of sizes l Copyright Rudra Dutta, NCSU, Fall, 2007 20

Approximations Practically, very close may be as good as there l “Close” is defined as fraction of or difference from the optimal objective value l – Must be constant An approximation to an NPC problem which is in P is quite valuable l May be possible to customize the algorithm to obtain any desired approximation ratio l – l Polynomial Time Approximation Scheme However, many problems are NP-approximable Copyright Rudra Dutta, NCSU, Fall, 2007 21

Networking Context Many network design problems are complex l It is important to know whether optimal solutions may be tractably attempted l If not, approximations/heuristics may be attempted l NPC reduction method may provide an insight into profitable heuristic methods l Copyright Rudra Dutta, NCSU, Fall, 2007 22

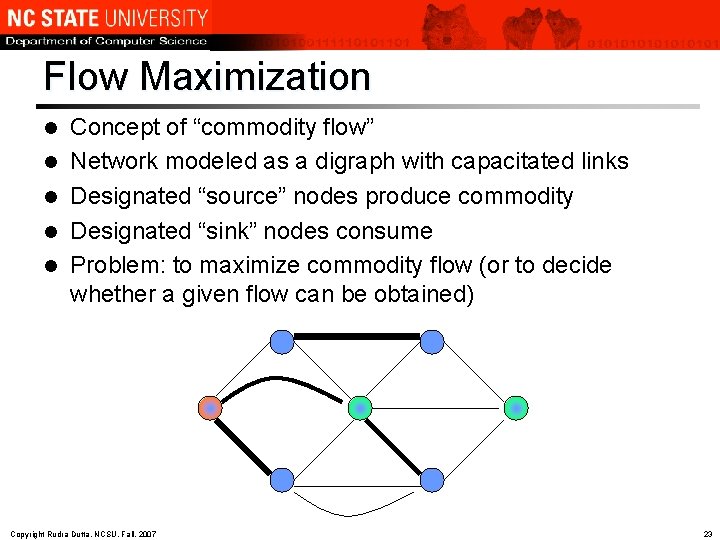
Flow Maximization l l l Concept of “commodity flow” Network modeled as a digraph with capacitated links Designated “source” nodes produce commodity Designated “sink” nodes consume Problem: to maximize commodity flow (or to decide whether a given flow can be obtained) Copyright Rudra Dutta, NCSU, Fall, 2007 23

Flow Augmentation Algorithm l Max-flow Min-cut theorem The maximal amount of flow is equal to the capacity of a minimal cut – Formalization of the concept of bottleneck – Equivalent: no augmenting path can be found in the residual network l Residual - update capacity by subtracting flow l – May create positive capacity links out of zero capacity links (reverse flow) Augmenting path - path with positive capacity l Iterate to get maximum flow l Copyright Rudra Dutta, NCSU, Fall, 2007 24

Minimum Cost 1 -Commodity Flow l More practical problem Every link has cost as well as capacity – Posed with integer cost, supply/demand, capacity – Total supply equals total demand – l Question: can a given flow to/from s-/d-nodes be achieved within a given cost bound? – l Feasibility can be checked using max-flow approach Polynomial problem Several known polynomial time algorithms – Capacity scaling algorithm, e. g. – Simpler version: successive shortest path algorithm – l – Not strictly polynomial Refer to excerpt from Ahuja, Magnanti, Orlin Copyright Rudra Dutta, NCSU, Fall, 2007 25

Successive Shortest Path Mass balance: amounts of incoming of outgoing flow balance to total source or sink requirement of a node (zero if it is neither source nor sink) l Pseudoflow: flow function which obeys nonnegativity and capacity, but not mass balance l – Imbalance of a node: difference in flow in and out, corrected by supply/demand Potential: a value maintained for each node l Keep a pseudoflow and a potential vector, both initially zero l Initially all imbalances are equal to supply l Copyright Rudra Dutta, NCSU, Fall, 2007 26

Successive Shortest Path Choose a node k with excess and a node l with deficit l Calculate shortest path distances from k to all other nodes l Use edge costs corrected by node potential differences as costs – Update node potentials, reducing by shortest path cost from k – l Choose a particular path from k to l – l Augment the pseudoflow as much as possible, not exceeding capacity of any link or imbalance of k or l Repeat until no imbalance exists Copyright Rudra Dutta, NCSU, Fall, 2007 27

Multi-Commodity Flow Capacitated, cost-weighted digraph, as before l Now there are distinct “commodities” l – l Producers and consumers for each commodity must be matched, cannot be interchanged In particular, every node may generate a unique commodity for every other node – N x (N-1) distinct commodities Question: can a given set of commodity flows to/from s-/d-nodes be achieved within a given cost bound? l Significantly more difficult l In fact, NP-complete l Optimization version often of practical interest l Copyright Rudra Dutta, NCSU, Fall, 2007 28

Optimization Copyright Rudra Dutta, NCSU, Fall, 2007

Optimization Another name for minimization or maximization l Usually used when quantity (function) is l Built of complex combinations of variables – Does not vary smoothly like “normal” functions – l Conceptual difficulty in describing the problem Basic entities may be many, of different kinds – Consider the multi-commodity flow problem – Or the simpler version we attempted in class – Contrast with, say, Traveling Salesman Problem – Copyright Rudra Dutta, NCSU, Fall, 2007 30

Elements l Parameters Given input values, constant for a given instance – The list of weights and values in Knapsack, e. g. – l Variables Required output values in solution – List of “yes/no” answers for each object – l Constraints Reflection of characteristics of real-life problem – “Knapsack cannot hold more than 50 lb and remain intact” – l Objective Definition of quantity to be maximized or minimized – Total value of objects tagged “yes” in answer – Copyright Rudra Dutta, NCSU, Fall, 2007 31

Static Optimization Distinct from dynamic or stochastic optimization l Mathematical programming problems l Minimize F(x) – Subject to x S – l l l x is the variable vector S represents constraints (with parameters) F() is the objective function S is a (feasible) solution set or optimization space If S is empty the problem is infeasible We are often interested in the specific class of ((Mixed) Integer ) Linear Programming problems Copyright Rudra Dutta, NCSU, Fall, 2007 32

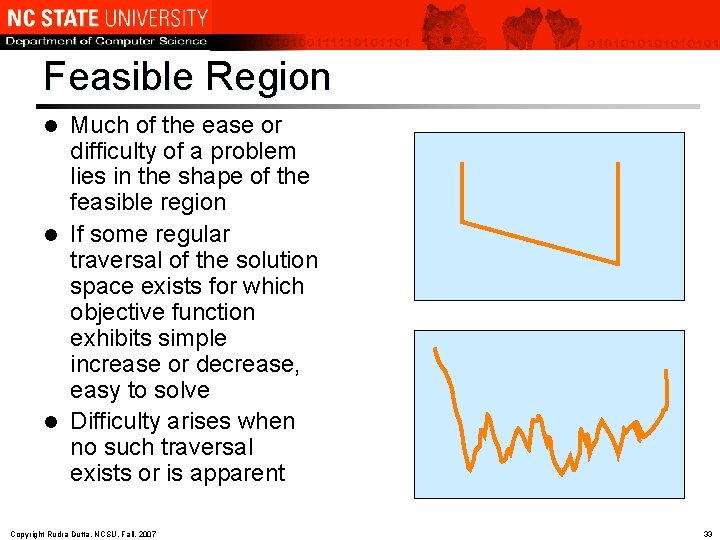
Feasible Region Much of the ease or difficulty of a problem lies in the shape of the feasible region l If some regular traversal of the solution space exists for which objective function exhibits simple increase or decrease, easy to solve l Difficulty arises when no such traversal exists or is apparent l Copyright Rudra Dutta, NCSU, Fall, 2007 33

Convexity l S is convex if for all points x, y S, the whole segment joining x and y belongs to S – l {ax + (1 - a) y : 0 a 1} S A function f on S is a convex function if x, y S, a [0, 1] – f (ax + (1 - a) y) af (x) + (1 - a) f (y) – Concavity, strictly convex (concave) l If F and S are both convex, such problems have nice properties and are easier to solve l Discrete analogue to convexity l Pareto optimal - for multiple objectives Fi, a solution such that no other exists l – At least as good for all, and better for at least one objective Copyright Rudra Dutta, NCSU, Fall, 2007 34

Gradient and Differentiability l Gradient - generalization of derivative – Vector of partial (directional) derivatives – l If a point is a local minimum, gradient is zero at that point – l For convex functions, an interior point which is a local minimum is also a global minimum Hessian - square matrix of second order partial derivatives – If Hessian is PSD at an interior gradient zero point, that point is locally optimal Copyright Rudra Dutta, NCSU, Fall, 2007 35

Interior and Border Optima Copyright Rudra Dutta, NCSU, Fall, 2007 36

Karush-Kuhn-Tucker Conditions l Often local minima are attained at border points, not interior points – Must be characterized by other means l Let S be defined by (all hi and gj differentiable): l Then multipliers m (unconstrained sign) and l (nonnegative) exist such that: Copyright Rudra Dutta, NCSU, Fall, 2007 37

Further Concepts l l l Perturbation - sensitivity Gradient descent - numerical methods Duality Subgradient Maximization Relaxation Copyright Rudra Dutta, NCSU, Fall, 2007 38

Relaxation l Removing some constraints - relaxing Makes the solution space larger – But may make the problem “easier” – Provides bound on optimal objective of original – l Removing integer constraints – l LP is possible to solve, so beneficial if linear system Lagrangian relaxation – – – Solving the dual of the given problem Convert one or more or all the constraints into “violation costs” in objective For given multipliers, often easy to solve Now optimize new cost get values for multipliers Results regarding the “duality gap”, “complementary slack” Copyright Rudra Dutta, NCSU, Fall, 2007 39

Duality and Lagrangian Primal: Lagrangian Function: Dual Problem: Copyright Rudra Dutta, NCSU, Fall, 2007 40

Example: Knapsack l Consider the knapsack instance {(8, 16), (9, 20), (5, 12), (4, 10)} (value, weight) – Weight bound 42, optimization version – l Optimization formulation: Maximize 8 x 1 + 9 x 2 + 5 x 3 + 4 x 4 – S. t. 16 x 1 + 20 x 2 + 12 x 3 + 10 x 4 ≤ 42 – xi {0, 1} i – Not obvious (in general NPC, as we know) l But remove the inequality constraint l Now trivial, set all xi = 1 – Clearly a bound, but not a very good one – Next? – Copyright Rudra Dutta, NCSU, Fall, 2007 41

Example: Knapsack (contd. ) l Now consider the following problem: to maximize: 8 x 1 + 9 x 2 + 5 x 3 + 4 x 4 + l (42 - 16 x 1 - 20 x 2 - 12 x 3 - 10 x 4) – Each xi still required to be from {0, 1} – l For any given l, this is likely to be much easier In general, eliminate constraints one by one into “violation cost” – Unique approach: eliminate all constraints except bounds – Specifically, all inequality constraints – Reduced to equality problem: hence “Lagrangian” – l Now the overall problem is one of choosing l so as to minimize this cost – l Likely to be amenable to numerical search Example adapted from CMU webpage, Michael Trick Copyright Rudra Dutta, NCSU, Fall, 2007 42

(Integer) Linear Programs l Linear - all constraints can be posed as only linear combinations of variables – For long complexity was open - thought NPI l – Comparatively recently resolved to be polynomial Simplex is exponential but usually runs faster If the polyhedron of feasible region has extreme points, and an optimal exists, an extreme optimal exists l Strictly polynomial methods (elliptical, interior points) exist l l Integer - all (pure) or some (mixed) variables are constrained to be integers Jump in practical difficulty level - NPC – Branch-and-bound, dynamic programing, … – l Relaxation of integer constraints is an obvious way to solve practically Need to round off solutions – But if integer constraints are binary, not a good method – In general binary problems are harder and “best” formulations are not easy to characterize – Copyright Rudra Dutta, NCSU, Fall, 2007 43

Network Context l Many networking problems are linear programs Commodity flow problems – Objective function sometimes poses problems – Integer constraints often appear – We are interested not only in optimal value, but also actual solution l Practically, solving ILP is not a good approach l However, domain specific knowledge may allow specific relaxation or other approach l Copyright Rudra Dutta, NCSU, Fall, 2007 44

Multi-Commodity Flow Formulation l Parameters – – – l n : number of nodes i A : set of all links (i, j) uij : bitrate of link cij : cost per bit on link bkl : traffic demand from node k to node l j Variables – l l k xklij : traffic from k to l using link from i to j Goal: minimize total cost Source: Bertsimas and Tsitsilkis Copyright Rudra Dutta, NCSU, Fall, 2007 45

Multi-Commodity Flow Formulation i Copyright Rudra Dutta, NCSU, Fall, 2007 46

Node-Link and Link-Path Two ways of formulating the same thing l Node-link - nodes, links are entities of interest l Focus on traffic demand to and from nodes, on links – Bridging variable - demand between nodes on links – Like previous example – l Link-path - links, paths are entities of interest Demand is still between nodes – For each given demand node pair, list all paths – Assign variable to path traffic flow (implicitly identifies demand) – For each link, sum up path flow variables, and constrain with capacities – Copyright Rudra Dutta, NCSU, Fall, 2007 47

Programming Assignment Implement the flow augmentation algorithm for single-commodity flow maximization l Implement the successive shortest path algorithm for minimum-cost commodity flow l Realize the ILP formulation for multi-commodity flow in CPLEX l Copyright Rudra Dutta, NCSU, Fall, 2007 48