CS 5321 Numerical Optimization 02 10302020 Fundamental of

CS 5321 Numerical Optimization 02 10/30/2020 Fundamental of Unconstrained Optimization 1

What is a solution? l l A point x* is a global minimizer if f (x*) f (x) for all x. A point x* is a local minimizer if there is a neighborhood N of x* such that f (x*) f (x) for all x N. 10/30/2020 2

Necessary conditions l If x* is a local minimizer of f and 2 f exists and is continuously differentiable in an open neighborhood of x*, then f (x*) = 0 and 2 f (x*) is positive semidefinite l 10/30/2020 x* is called a stationary point if f (x*) = 0. 3

Convexity l l When f is convex, any local minimizer x* is a global minimizer of f. In addition, if f is differentiable, then any stationary point x* is a global minimizer of f. 10/30/2020 4

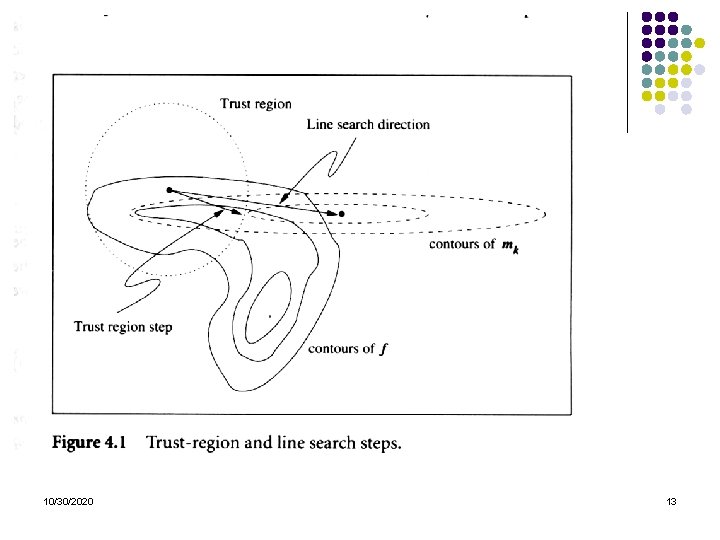
Two strategies Line search method (chap 3) 1. Given a point xk, find a descent direction pk. Find the step length αk to minimize f (xk+αkpk) Next point xk+1= xk+ αkpk. a) b) c) Trust region method (chap 4) 2. a) b) c) 10/30/2020 For a function f, construct a model function mk. Define a trust region R(xk) inside which f ≈ mk. Solve the minimization problem: minpmk(xk+p) where p lies inside R(xk) 5

Methods to find descent directions for line search l Method 1: the steepest descent method l l l Method 2: the Newton’s method l l l First order approximation Linear convergence (global convergence) Second order approximation Quadratic convergence (local convergence) Method 3: the conjugate gradient method (chap 5) 10/30/2020 6

The steepest descent method l The steepest descent method (first order approx) l l From the Taylor’s expansion, f (x k + p) ¼ f (x k ) + p. T r f (x k ) To minimize , such that p = ¡ r f (x k )=kr f (x k )k l 10/30/2020 kpk = 1 p. T r f (x k ) = kpkkr f (x k )k cosµ Because Minimization is at cos =− 1 7

The Newton’s method l The Newton’s method (second order approx) l l l Assume the Hessian is positive definite From the Taylor’s expansion, f (x k + p) ¼ f (x k ) + p. T r f (x k ) + 1 p. T r 2 f (x k )p 2 r f (x k + p) = 0 The minimization of f (xk+p) is at l l 10/30/2020 Note p is the variable. f (xk), 2 f (xk) are constants. r f (x k + p) ¼ r f (x k ) + r 2 f (x k )p = 0 Newton’s direction is p. N = ¡ (r 2 f (x k )) ¡ 1 r f (x k ) 8

p. N = ¡ (r 2 f (x k )) ¡ 1 r f (x k ) Substitute f (x k + p) ¼ f (x k ) + p. T r f (x k ) + f (x k + p. N ) (x k )p 1 N T 2 (p ) r f (x k )p. N 2 f (x k ) ¡ r f (x k ) T (r 2 f (x k )) ¡ 1 r f (x k ) + 1 r f (x k ) T (r 2 f (x k )) ¡ 1 r f (x k ) 2 1 f (x k ) ¡ r f (x k ) T (r 2 f (x k )) ¡ 1 r f (x k ) 2 f (x k ) ¼ f (x k ) + (p. N ) T r f (x k ) + = = · 10/30/2020 1 p. T r 2 f 2 to 9

Variations of Newton’s method l The Hessian matrix may be indefinite, illconditioned, or even singular. l l The computation of Hessian is expensive l l Modified Newton’s methods. (chap 3) Quasi-Newton methods (chap 6) The inverse of Hessian is expensive l 10/30/2020 Inexact Newton’s method (chap 7) 10

The conjugate gradient method l The current search direction pk is a linear combination of previous search direction pk-1 and current gradient pk = ¡ r f (x k ) + ¯k pk ¡ l 1 Scalar k is given such that pk and pk-1 are conjugate. 10/30/2020 11

Models for trust-region method l Linear model: l Quadratic model: f (x k + p) ¼ f (x k ) + p. T r f (x k ) + l 10/30/2020 1 p. T r 2 f 2 (x k )p All variations of Newton’s method can be applied. 12

10/30/2020 13