COMP 4200 Expert Systems Dr Christel Kemke Department

COMP 4200: Expert Systems Dr. Christel Kemke Department of Computer Science University of Manitoba © C. Kemke Inexact Reasoning 1

Inexact Reasoning References: Jackson, Chapter 19, Truth Maintenance Systems Giarratano and Riley, Chapters 4 and 5 Luger and Stubblefield 'Artificial Intelligence', Addison. Wesley, 2002, Chapter 7 © C. Kemke Inexact Reasoning 2

Knowledge & Inexact Reasoning inexact knowledge (truth of not clear) incomplete knowledge (lack of knowledge about ) defaults, beliefs (assumption about truth of ) contradictory knowledge ( true and false) vague knowledge (truth of not 0/1) © C. Kemke Inexact Reasoning 3

Inexact Reasoning CF Theory - uncertainty about facts and conclusions Fuzzy - vagueness truth not 0 or 1 but graded (membership fct. ) Truth Maintenance - beliefs, defaults assumptions about facts, can be revised Probability Theory - likelihood of events statistical model of knowledge © C. Kemke Inexact Reasoning 4

Inexact Reasoning not necessary. . . NOT necessary when assuming: complete knowledge about the "world" no contradictory facts or rules everything is either true or false This corresponds formally to a complete consistent theory in First-Order Logic, i. e. everything you have to model is contained in theory, i. e. your theory or domain model is complete facts are true or false (assuming your rules are true) your sets of facts and rules contain no contradiction (are consistent) © C. Kemke Inexact Reasoning 5

Exact Reasoning: Theories in First-Order Predicate Logic Theory (Knowledge Base) given as a set of well-formed formulae. Formulae include facts like mother (Mary, Peter) and rules like mother (x, y) child (y, x) Reasoning based on applying rules of inference of first-order predicate logic, like Modus Ponens: p, p q q If p and p q given then q can be inferred (proven) © C. Kemke Inexact Reasoning 6

Forms of Inexact Knowledge uncertainty (truth not clear) incomplete knowledge (lack of knowledge) assume P is true, as long as there is no counter-evidence (i. e. that ¬P is true) assume P is true with Certainty Factor contradictory knowledge (true and false) P true or false not known ( defaults) defaults, beliefs (assumptions about truth) probabilistic models, multi-valued logic (true, false, don't know, . . . ), certainty factor theory inconsistent fact base; somehow P and ¬P true vague knowledge (truth value not 0/1; not crisp sets) © C. Kemke graded truth; fuzzy sets Inexact Reasoning 7

Inexact Knowledge - Example Person A walks on Campus towards the bus stop. A few hundred yards away A sees someone and is quite sure that it's his next-door neighbor B who usually goes by car to the University. A screams B's name. Q: Which forms of inexact knowledge and reasoning are involved here? default - A wants to take a bus belief, (un)certainty - it's the neighbor B probability, default, uncertainty - the neighbor goes home by car default - A wants to get a lift default - A wants to go home © C. Kemke Inexact Reasoning 8

Examples of Inexact Knowledge Person A walks on Campus towards the bus stop. A few hundred yards away A sees someone and is quite sure that it's his nextdoor neighbor B who usually goes by car to the University. A screams B's name. Fuzzy - a few hundred yards define a mapping from "#hundreds" to 'few', 'many', . . . not uncertain or incomplete but graded, vague Probabilistic - the neighbor usually goes by car probability based on measure of how often he takes car; calculates always p(F) = 1 - p(¬F) Belief - it's his next-door neighbor B "reasoned assumption", assumed to be true Default - A wants to take a bus assumption based on commonsense knowledge © C. Kemke Inexact Reasoning 9

Dealing with Inexact Knowledge Methods for representing and handling: 1. incomplete knowledge: defaults, beliefs Ø Truth Maintenance Systems (TMS); non-monotonic reasoning 2. contradictory knowledge: contradictory facts or different conclusions, based on defaults or beliefs Ø TMS, Certainty Factors, . . . , multi-valued logics 3. uncertain knowledge: hypotheses, statistics Ø Certainty Factors, Probability Theory 4. vague knowledge: "graded" truth Ø Fuzzy, rough sets 5. inexact knowledge and reasoning Ø © C. Kemke involves 1 -4; clear 0/1 truth value cannot be assigned Inexact Reasoning 10

Truth Maintenance Systems © C. Kemke Inexact Reasoning 11

Truth Maintenance Necessary when changes in the fact-base lead to inconsistency / incorrectness among the facts non-monotonic reasoning A Truth Maintenance System tries to adjust the Knowledge Base or Fact Base upon changes to keep it consistent and correct. A TMS uses dependencies among facts to keep track of conclusions and allow revision / retraction of facts and conclusions. © C. Kemke Inexact Reasoning 12

Non-monotonic Reasoning non-monotonic reasoning § The set of currently valid (believed) facts does NOT increase monotonically. § Adding a new fact might lead to an inconsistency which requires the removal of one of the contradictory facts. § Thus, the set of true (or: believed as true) facts can shrink and grow with reasoning. § This is why it’s called “non-monotonic reasoning”. § In classical logic (first-order predicate logic) this does not happen. Once a fact is asserted, it’s forever true. © C. Kemke Inexact Reasoning 13

Non-monotonic Reasoning - Example: non-monotonic reasoning Your are a student, it's 8 am , you are in bed. You slip out of your dreams and think: Today is Sunday. No classes today. l don't have to get up. You go back to sleep. You wake up again. It's 9: 30 am now and it is slowly coming to your mind: Today is Tuesday. What an unpleasant surprise. P 1 = today-is-Tuesday P 3 = have-class-at-10 am P 5 = have-to-get-up © C. Kemke P 2 = today-is-Sunday P 4 = no-classes P 6 = can-stay-in-bed Inexact Reasoning 14

Non-monotonic Reasoning - Example P 1 = today-is-Tuesday P 3 = have-class-at-10 am P 5 = have-to-get-up P 1 P 3 P 5 P 2 P 4 P 6 P 2 = today-is-Sunday P 4 = no-classes P 6 = can-stay-in-bed Assume: P 1 and P 2, P 3 and P 4, P 5 and P 6 are mutually exclusive, i. e. P 1 P 2, P 3 P 4, P 5 P 6 assume P 2; conclude P 1 ; P 4 ; P 3 ; P 6 ; P 5 assume P 1; conclude P 2 ; P 3 ; P 4 ; P 5 ; P 6 © C. Kemke Inexact Reasoning 15

Truth Maintenance Theories TMS are often based on dependency-directed backtracking to the point in reasoning where a wrong assumption was used. Mc. Allester (1978, 1980) “propositional constraint propagation” employs a dependency network which reflects the justification of conclusions of new facts Doyle (1979) justification based Truth Maintenance System © C. Kemke Inexact Reasoning 16

Truth Maintenance Theories - Mc. Allester “propositional constraint propagation” § network representing conclusions, where § proposition-nodes are connected if one of the nodes is a reason for concluding the other node. Example: p q (p q) If p is known to be true, q can be concluded. Connections from p and p q to q mean that p and p q are reasons to conclude p. © C. Kemke Inexact Reasoning 17

Truth Maintenance Theories - Mc. Allester (1980) proposition-nodes are connected if one of the nodes is a reason for concluding the other node (simplified version). Example: Connections from p and p q to combination and then to q represent justification for q p q p © C. Kemke p q p q Inexact Reasoning 18

Truth Maintenance Theories - Doyle (1979) deals with beliefs as justified assumptions. As long as there is no contra-evidence for a fact (belief) we can assume that it is true. INp facts which support P; OUTp facts which prevent P. Distinguishes: Premises - always true (INp = OUTp = ) Deductions - derived (INp ; OUTp = ) Assumptions – depends (INp = ; OUTp ) © C. Kemke Inexact Reasoning 19

Truth Maintenance Theories - Doyle (1979) As long as there is no contra-evidence for a fact (belief) we can assume that it is true. Theory is based on the concept of Support-Lists (SL). A Support-List of a Fact (Belief) P specifies Facts (Beliefs) which support the conclusion of the Fact P or prevent its conclusion. The TMS maintains and updates the set of current Facts/Beliefs if changes occur. Uses justification networks, similar to Mc. Allester’s dependency networks. © C. Kemke Inexact Reasoning 20

Truth Maintenance in CLIPS 1 logical connection between condition- and action-part of a rule if logical-part of condition is not true anymore, consequence-fact in action-part is retracted (defrule fire-reaction (logical (fire-present)) => (assert (alarm-on))) When fire-present is true, alarm-on can be concluded. When fire-present is retracted, alarm-on will also be retracted. © C. Kemke Inexact Reasoning 21

Truth Maintenance in CLIPS 2 Dependencies (dependents <fact-index>) prints all current facts which depend on the indexed fact (are concluded from that fact) (dependencies <fact-index>) prints all current facts on which the indexed fact depends (from which the indexed fact can was concluded) dependents of fire-present alarm-on dependencies of fire-present none © C. Kemke Inexact Reasoning 22

Certainty Factor Theory © C. Kemke Inexact Reasoning 23

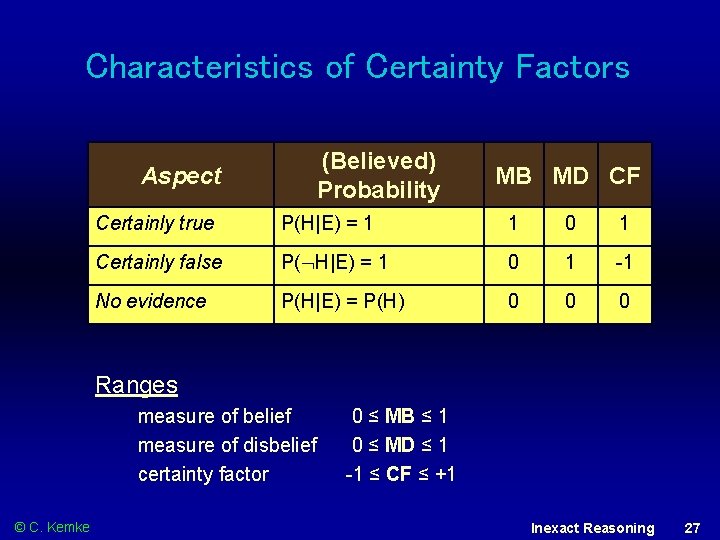
Certainty Factor Theory Certainty Factor CF of Hypothesis H ranges between -1 (denial of H) and +1 (confirmation of H) allows the ranking of hypotheses Based on measures of belief MB and disbelief MD MB is expressing the belief that H is true MD is expressing the belief that H is not true MB is not 1 -MD - it’s not like probabilities Experts determine values for MB, MD of H based on given evidence E subjective © C. Kemke Inexact Reasoning 24

Stanford Certainty Factor Theory Ø Certainty Factor CF of Hypothesis H is based on difference between Measure of Belief MB and Measure of Disbelief MD in hypothesis H, given evidence E. Certainty Factor of hypothesis H given evidence E: CF (H|E) = MB(H|E) – MD(H|E) Ø Ø -1 CF(H) 1 Can integrate different experts’ assessments. Basis to combine support/rejection for H within one rule and using different rules. © C. Kemke Inexact Reasoning 25

Stanford Certainty Factor Theory Remember the base rule for Certainty Factor CF (H|E) : CF (H|E) = MB(H|E) – MD(H|E) -1 CF(H) 1 Integrate Certainty Factors into reasoning. CF-value for H calculated using CFs of premises P in rule CF(H) = CF(P 1 and P 2) = min (CF(P 1), CF(P 2)) CF(H) = CF(P 1 or P 2) = max (CF(P 1), CF(P 2)) CF-value for H combined from different rules, experts, . . . CF(H) = CF 1 + CF 2 – CF 1∙ CF 2 if both CF 1, CF 2 > 0 CF(H) = CF 1 + CF 2 + CF 1∙ CF 2 if both CF 1, CF 2 0 CF(H) = CF 1 + CF 2 else 1 – min ( |CF 1|, |CF 2| ) © C. Kemke Inexact Reasoning 26

Characteristics of Certainty Factors (Believed) Probability Aspect MB MD CF Certainly true P(H|E) = 1 1 0 1 Certainly false P( H|E) = 1 0 1 -1 No evidence P(H|E) = P(H) 0 0 0 Ranges measure of belief measure of disbelief certainty factor © C. Kemke 0 ≤ MB ≤ 1 0 ≤ MD ≤ 1 -1 ≤ CF ≤ +1 Inexact Reasoning 27

Probability Theory © C. Kemke Inexact Reasoning 28

Basics of Probability Theory mathematical approach to process uncertain information sample space (event) set: S = {x 1, x 2, …, xn} collection of all possible events probability p(xi) is likelihood that the event xi S occurs non-negative values in [0, 1] total probability of the sample space is 1, p(xi , xi S) = 1 experimental probability subjective probability (CF Theories, like Dempster-Shafer, . . . ) © C. Kemke based on the frequency of events based on expert assessment Inexact Reasoning 29

Compound Probabilities for independent events do not affect each other in any way example: cards and events “hearts” and “queen” joint probability of independent events A and B P(A B) = |A B| / |S| = P(A) * P(B) where |S| is the number of elements in S union probability of independent events A and B P(A B) = P(A) + P(B) - P(A) * P (B) Situation in which either event occurs. Subtract probability of their accidental co-occurrence - P(A B) is already included in P(A)+P(B) and would otherwise be counted twice. © C. Kemke Inexact Reasoning 30

Compound Probabilities For mutually exclusive events can not occur together at the same time Examples: one dice and events “ 1” and “ 6”; one coin and events “heads” and “tail” joint probability of two different events A and B P(A B) = 0 Throw dice and show both “ 1” and “ 6” cannot happen. union probability of two events A and B P(A B) = P(A) + P(B) Throw coin and show either “heads” or “tail”. This is also called “special addition”. © C. Kemke Inexact Reasoning 31

Conditional Probabilities describes dependent events affect each other in some way Example: Throw dice twice; second throw has to give larger value than first throw. conditional probability of event A given that event B has already occurred P(A|B) = P(A B) / P(B) example: B = throw(x); A = throw(y>x) See next slide. © C. Kemke Inexact Reasoning 32

Conditional Probabilities Example: B = throw(x); A = throw(y>x) P(A|B) = P(throw x and then throw y with y>x) P(A|B) = P(A B) / P(B) P(A B) = P(throw x) P(throw y, y>x) = 1/6 (6 -x)) If x=5 then P(A B) = 1/6 (6 -5) = 1/36 If x=1 then P(A B) = 1/6 5 = 5/36 P(B) = P(throw x) = 1/6 P(A|B) = P(A B) / P(B) If x=1 then P(A|B) = 5/36*6 = 5/6 0. 8. . . If x=5 then P(A|B) = 5/36*1 = 5/36 0. 14 © C. Kemke Inexact Reasoning 33

Bayesian Approaches derive the probability of a cause given a symptom has gained importance recently due to advances in efficiency more computational power available better methods especially useful in diagnostic systems medicine, computer help systems inverse or a posteriori probability © C. Kemke inverse to conditional probability of an earlier event given that a later one occurred Inexact Reasoning 34

Bayes’ Rule for Single Event single hypothesis H, single event E P(H | E) = (P(E | H) * P(H)) / P(E) or P(H © C. Kemke | E) = (P(E | H) * P(H) / (P(E | H) * P(H) + P(E | H) * P( H) ) Inexact Reasoning 35

Example © C. Kemke Inexact Reasoning 36

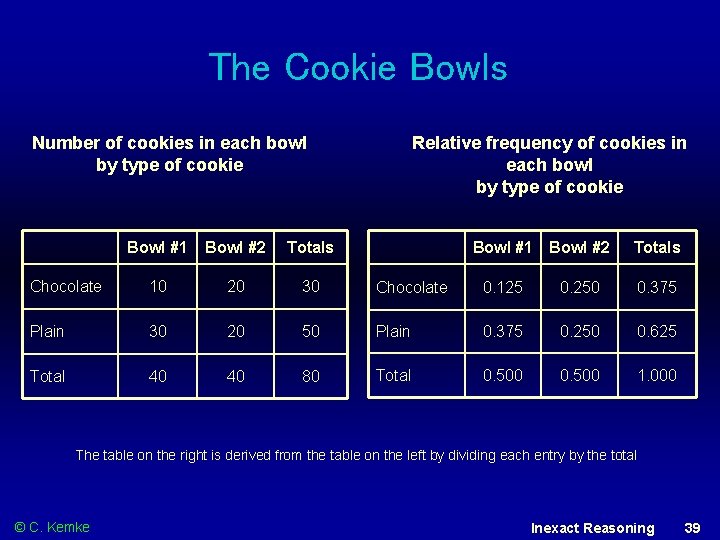
Fred and the Cookie Bowls Suppose there are two bowls full of cookies. Bowl #1 has 10 chocolate chip cookies and 30 plain cookies, while bowl #2 has 20 of each. Fred picks a bowl at random, and then picks a cookie at random. We may assume there is no reason to believe Fred treats one bowl differently from another, likewise for the cookies. The cookie turns out to be a plain one. How probable is it that Fred picked it out of bowl #1? From: http: //en. wikipedia. org/wiki/Bayes'_theorem © C. Kemke Inexact Reasoning 37

The Cookie Bowl Problem “What’s the probability that Fred picked bowl #1, given that he has a plain cookie? ” Event A is that Fred picked bowl #1. Event B is that Fred picked a plain cookie. Compute P(A|B). We need: P(A) - the probability that Fred picked bowl #1 regardless of any other information. Since Fred is treating both bowls equally, it is 0. 5. P(B) is the probability of getting a plain cookie regardless of any information on the bowls. It is computed as the sum of the probability of getting a plain cookie from a bowl multiplied by the probability of selecting this bowl. We know that the probability of getting a plain cookie from bowl #1 is 0. 75, and the probability of getting one from bowl #2 is 0. 5. Since Fred is treating both bowls equally the probability of selecting any one of the bowls is 0. 5 (see next slide). Thus, the probability of getting a plain cookie overall is 0. 75× 0. 5 + 0. 5× 0. 5 = 0. 625. P(B|A) is the probability of getting a plain cookie given that Fred has selected bowl #1. From the problem statement, we know this is 0. 75, since 30 out of 40 cookies in bowl #1 are plain. © C. Kemke Inexact Reasoning 38

The Cookie Bowls Number of cookies in each bowl by type of cookie Bowl #1 Bowl #2 Totals Chocolate 10 20 30 Plain 30 20 Total 40 40 Relative frequency of cookies in each bowl by type of cookie Bowl #1 Bowl #2 Totals Chocolate 0. 125 0. 250 0. 375 50 Plain 0. 375 0. 250 0. 625 80 Total 0. 500 1. 000 The table on the right is derived from the table on the left by dividing each entry by the total © C. Kemke Inexact Reasoning 39

Fred and the Cookie Bowl Given all this information, we can compute the probability of Fred having selected bowl #1 (event A) given that he got a plain cookie (event B), as such: As we expected, it is more than half. http: //en. wikipedia. org/wiki/Bayes'_theorem © C. Kemke Inexact Reasoning 40

Fuzzy Set Theory © C. Kemke Inexact Reasoning 41

Fuzzy Set Theory (Zadeh) Aimed to model and formalize "vague" Natural Language terms and expressions. Example: Peter is relatively tall. Define a set of fuzzy sets (predicates or categories), like tall, small. Each fuzzy subset has an associated membership function mapping (exact) domain values into a (graded) membership value. tall would be one fuzzy subset defined by such a function which takes the height (e. g. in inches) as input, and determines a fuzzy membership-value (between 0 and 1) for tall and small as output. © C. Kemke Inexact Reasoning 42

Fuzzy Set Membership Function If Peter is 6' high, and the fuzzy membership value of tall for 6' is 0. 9, then Peter is quite tall. © C. Kemke Inexact Reasoning 43

Review Inexact Reasoning © C. Kemke uncertain reasoning – uncertainty about facts and/or rules – CF Theory vagueness – truth not 0 or 1 - Fuzzy sets and Fuzzy logic beliefs, defaults – assumptions about truth, can be revised – non-monotonic reasoning, Truth Maintenance System likelihood of event – statistical model of knowledge Probability Theory Inexact Reasoning 44

Other Forms of Representing and Reasoning with Inexact Knowledge © C. Kemke Logics Explicit modeling of Belief- and Knows. Operators in Modal Logic or Autoepistemic Logic. Probabilistic Reasoning Bayes’ Theory Dempster-Shafer Theory Inexact Reasoning 45

© C. Kemke Inexact Reasoning 46