Classical Mechanics PHYS 2006 Tim Freegarde 2020 21

Classical Mechanics PHYS 2006 Tim Freegarde 2020 -21 Forum 08

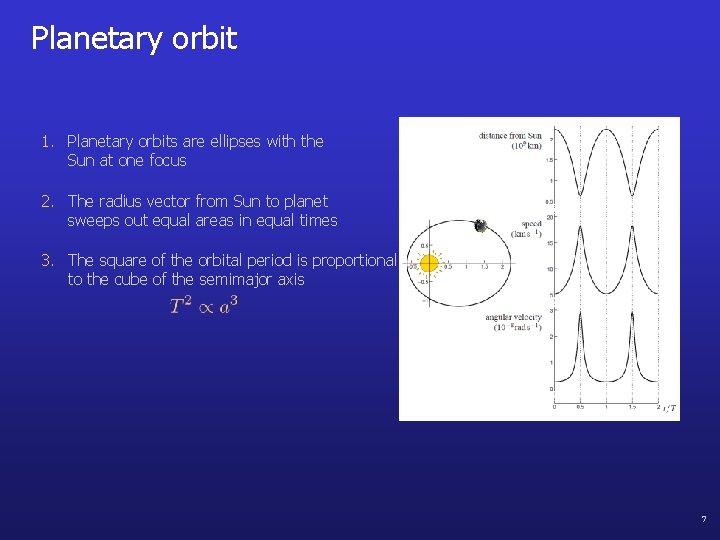
How to approach Kepler orbit problems 1. Planetary orbits are ellipses with the Sun at one focus 2. The radius vector from Sun to planet sweeps out equal areas in equal times 3. The square of the orbital period is proportional to the cube of the semimajor axis • Sun / C of M is at focus, not centre, of ellipse • at aphelion and perihelion, • conservation of energy • conservation of angular momentum • Johannes Kepler (1571 -1630) 2

Elliptical orbit • eccentricity • constant • semi latus rectum • polar equation • Cartesian equation • semimajor axis • semiminor axis • total energy 3

2015/16 exam, B 4 4

2015/16 exam, B 4 5

2015/16 exam, B 4 6

Planetary orbit 1. Planetary orbits are ellipses with the Sun at one focus 2. The radius vector from Sun to planet sweeps out equal areas in equal times 3. The square of the orbital period is proportional to the cube of the semimajor axis 7

Newton’s law of Universal Gravitation • Exact analogy of Coulomb electrostatic interaction • gravitational force between two masses and • gravitational field • gravitational potential • a spherically-symmetric mass distribution has the same external field as a point mass of equal magnitude at the sphere’s centre • inertial mass = gravitational mass 8

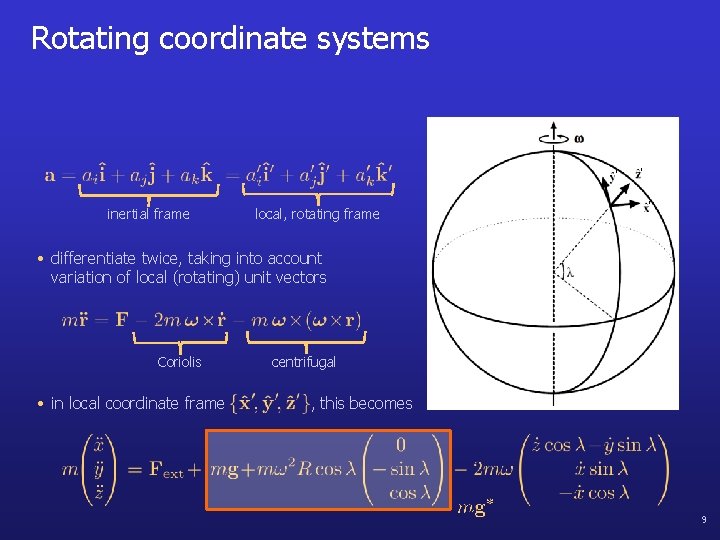
Rotating coordinate systems ' inertial frame local, rotating frame ' ' • differentiate twice, taking into account variation of local (rotating) unit vectors Coriolis • in local coordinate frame centrifugal , this becomes 9

Coriolis effect: free-fall 10

Cannon shell 11

Cannon shell 12

Cannon shell 13

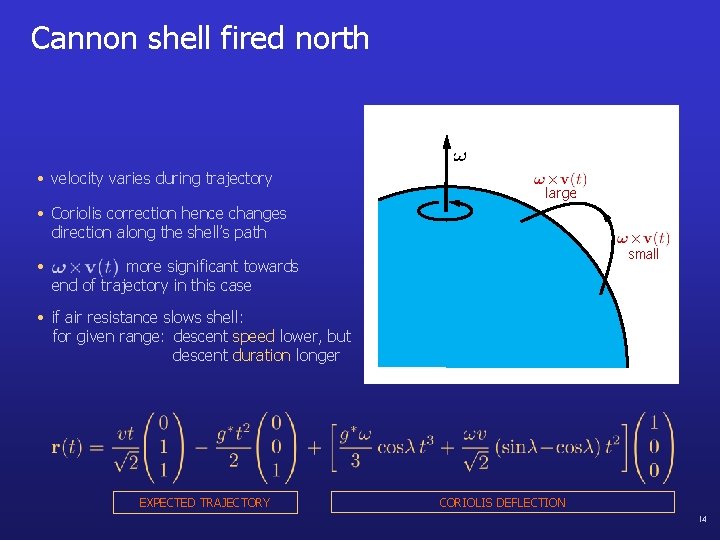
Cannon shell fired north • velocity varies during trajectory large • Coriolis correction hence changes direction along the shell’s path • small more significant towards end of trajectory in this case • if air resistance slows shell: for given range: descent speed lower, but descent duration longer EXPECTED TRAJECTORY CORIOLIS DEFLECTION 14

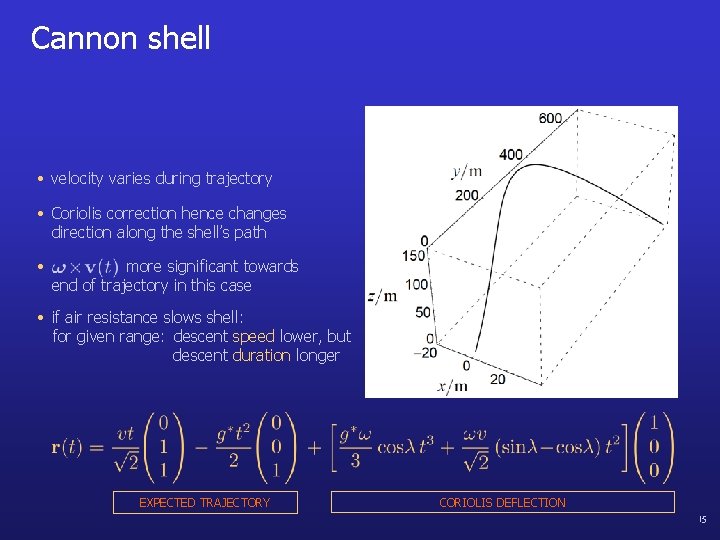
Cannon shell • velocity varies during trajectory • Coriolis correction hence changes direction along the shell’s path • more significant towards end of trajectory in this case • if air resistance slows shell: for given range: descent speed lower, but descent duration longer EXPECTED TRAJECTORY CORIOLIS DEFLECTION 15

Cannon shell • velocity varies during trajectory • Coriolis correction hence changes direction along the shell’s path • more significant towards end of trajectory in this case • if air resistance slows shell: for given range: descent speed lower, but descent duration longer EXPECTED TRAJECTORY CORIOLIS DEFLECTION 16

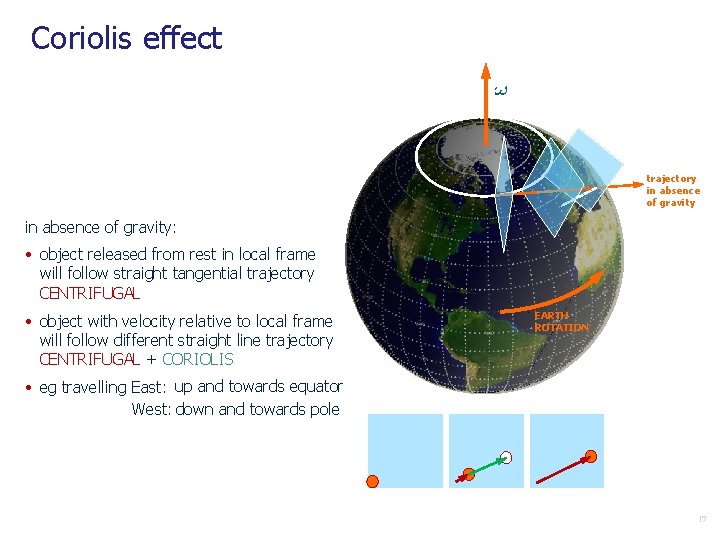
Coriolis effect trajectory in absence of gravity: • object released from rest in local frame will follow straight tangential trajectory CENTRIFUGAL • object with velocity relative to local frame will follow different straight line trajectory CENTRIFUGAL + CORIOLIS EARTH ROTATION • eg travelling East: up and towards equator West: down and towards pole 17

Classical Mechanics PHYS 2006 Tim Freegarde