Treatment of Uncertainties PHYS 244 and PHYS 246

Treatment of Uncertainties PHYS 244 and PHYS 246 Uncertainty 1

Types of Uncertainties Random Uncertainties: result from the randomness of measuring instruments. They can be dealt with by making repeated measurements and averaging. One can calculate the standard deviation of the data to estimate the uncertainty. Systematic Uncertainties: result from a flaw or limitation in the instrument or measurement technique. Systematic uncertainties will always have the same sign. For example, if a meter stick is too short, it will always produce results that are too long. Uncertainty 2

Accuracy vs. Precision Accurate: means correct. An accurate measurement correctly reflects the size of the thing being measured. Precise: repeatable, reliable, getting the same measurement each time. A measurement can be precise but not accurate. Uncertainty 3

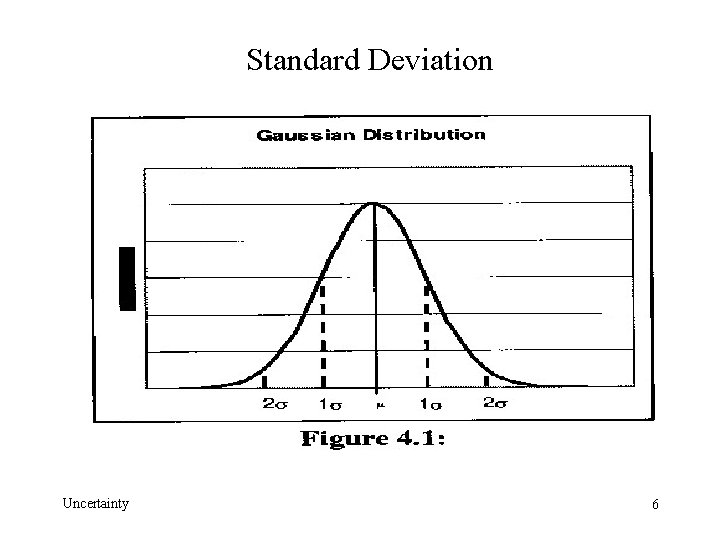
Standard Deviation The average or mean of a set of data is The formula for the standard deviation given below is the one used by Microsoft Excel. It is best when there is a small set of measurements. The version in the book divides by N instead of N-1. Unless you are told to use the above function, you may use the Excel function ‘=stdev(B 2: B 10)’ Uncertainty 4

Absolute and Percent Uncertainties If x = 99 m ± 5 m then the 5 m is referred to as an absolute uncertainty and the symbol σx (sigma) is used to refer to it. You may also need to calculate a percent uncertainty ( %σx): Please do not write a percent uncertainty as a decimal ( 0. 05) because the reader will not be able to distinguish it from an absolute uncertainty. Uncertainty 5

Standard Deviation Uncertainty 6

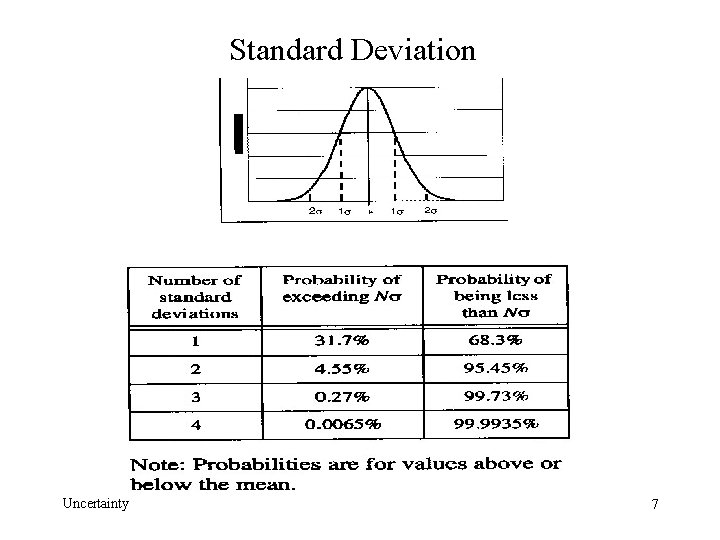
Standard Deviation Uncertainty 7

Expressing Results in terms of the number of σ • In this course we will use σ to represent the uncertainty in a measurement no matter how that uncertainty is determined • You are expected to express agreement or disagreement between experiment and the accepted value in terms of a multiple of σ. • For example if a laboratory measurement the acceleration due to gravity resulted in g = 9. 2 ± 0. 2 m / s 2 you would say that the results differed by 3σ from the accepted value and this is a major disagreement • To calculate Nσ Uncertainty 8

Propagation of Uncertainties with Addition or Subtraction If z = x + y or z = x – y then the absolute uncertainty in z is given by Example: Uncertainty 9

Propagation of Uncertainties with Multiplication or Division If z = x y or z = x / y then the percent uncertainty in z is given by Example: Uncertainty 10

Propagation of Uncertainties in mixed calculations If a calculation is a mixture of operations, you propagate uncertainties in the same order that you perform the calculations. Uncertainty 11

Uncertainty resulting from averaging N measurements If the uncertainty in a single measurement of x is statistical, then you can reduce this uncertainty by making N measurements and averaging. Example: A single measurement of x yields x = 12. 0 ± 1. 0, so you decide to make 10 measurements and average. In this case N = 10 and σx = 1. 0, so the uncertainty in the average is This is not true for systematic uncertainties- if your meter stick is too short, you don’t gain anything by repeated measurements. Uncertainty 12

Special Rule: Uncertainty when a number is multiplied by a constant Example: If x = 12 ± 1. 0 = 12. 0 ± 8. 3 % and z = 2 x, then z = 24. 0 ± 8. 3 % or z = 24 ± 2. It should be noted that you would get the same result by multiplying 2 (12 ± 1. 0)= 24 ± 2. This is actually a special case of the rule for multiplication and division. You can simply assume that the uncertainty in the constant is just zero and get the result given above. Uncertainty 13

Uncertainty when a number is raised to a power If z = xn then %σz = n ( % σx ) Example: If z = 12 ± 1. 0 = 12. 0 ± 8. 3 % then Uncertainty 14

Uncertainty when calculation involves a special function For a special function, you add and subtract the uncertainties from the value and calculate the function for each case. Then plug these numbers into the function. Example: If θ = 120 ± 2. 00 sin(140) = 0. 242 sin(120) = 0. 208 sin(100) = 0. 174 0. 034 And thus sin(120 ± 20 ) = 0. 208 ± 0. 034 Uncertainty 15

Percent Difference Calculating the percent difference is a useful way to compare experimental results with the accepted value, but it is not a substitute for a real uncertainty estimate. Example: Calculate the percent difference if a measurement of g resulted in 9. 4 m / s 2. Uncertainty 16