Relativistic Classical Mechanics XIX century crisis in physics

























































- Slides: 65

Relativistic Classical Mechanics

XIX century crisis in physics: some facts • Maxwell: equations of electromagnetism are not invariant under Galilean transformations • Michelson and Morley: the speed of light is the same in all inertial systems James Clerk Maxwell (1831 -1879) Albert Abraham Michelson (1852 – 1931) Edward Williams Morley (1838 – 1923)

Postulates of the special theory • 1) The laws of physics are the same to all inertial observers • 2) The speed of light is the same to all inertial observers • Formulation of physics that explicitly incorporates these two postulates is called covariant • The space and time comprise a single entity: spacetieme • A point in spacetime is called event • Metric of spacetime is non-Euclidean 7. 1

Tensors • Tensor of rank n is a collection of elements grouped through a set of n indices • Scalar is a tensor of rank 0 • Vector is a tensor of rank 1 • Matrix is a tensor of rank 2 • Etc. • Tensor product of two tensors of ranks m and n is a tensor of rank (m + n) • Sum over a coincidental index in a tensor product of two tensors of ranks m and n is a tensor of rank (m + + n – 2) 7. 5

Tensors • Tensor product of two vectors is a matrix • Sum over a coincidental index in a tensor product of two tensors of ranks 1 and 1 (two vectors) is a tensor of rank 1 + 1 – 2 = 0 (scalar): scalar product of two vectors • Sum over a coincidental index in a tensor product of two tensors of ranks 2 and 1 (a matrix and a vector) is a tensor of rank 2 + 1 – 2 = 1 (vector) • Sum over a coincidental index in a tensor product of two tensors of ranks 2 and 2 (two matrices) is a tensor of rank 2 + 2 – 2 = 2 (matrix) 7. 5

Metrics, covariant and contravariant vectors • Vectors, which describe physical quantities, are called contravariant vectors and are marked with superscripts instead of a subscripts • For a given space of dimension N, we introduce a concept of a metric – N x N matrix uniquely defining the symmetry of the space (marked with subscripts) • Sum over a coincidental index in a product of a metric and a contravariant vecor is a covariant vector or a 1 -form (marked with subscripts) • Magnitude: square root of the scalar product of a contravariant vector and its covariant counterpart 7. 4 7. 5

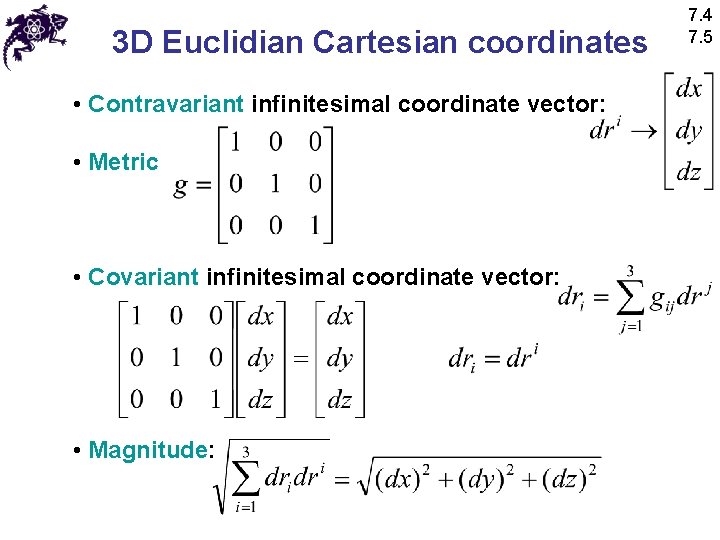
3 D Euclidian Cartesian coordinates • Contravariant infinitesimal coordinate vector: • Metric • Covariant infinitesimal coordinate vector: • Magnitude: 7. 4 7. 5

3 D Euclidian spherical coordinates • Contravariant infinitesimal coordinate vector: • Metric • Covariant infinitesimal coordinate vector: • Magnitude: 7. 4 7. 5

Hilbert space of quantum-mechanical wavefunctions • Contravariant vector (ket): • Covariant vector (bra): • Magnitude: David Hilbert (1862 – 1943) • Metric: 7. 4 7. 5

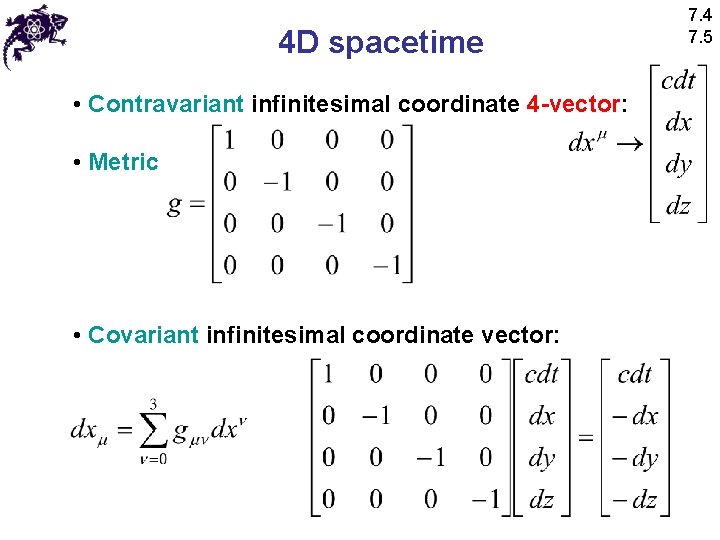
4 D spacetime • Contravariant infinitesimal coordinate 4 -vector: • Metric • Covariant infinitesimal coordinate vector: 7. 4 7. 5

4 D spacetime • Magnitude: • This magnitude is called differential interval • Interval (magnitude of a 4 -vector connecting two events in spacetime): • Interval should be the same in all inertial reference frames • The simplest set of transformations that preserve the invariance of the interval relative to a transition from one inertial reference frame to another: Lorentz transformations 7. 4 7. 5

7. 2 Lorentz transformations • We consider two inertial reference frames S and S’; relative velocity as measured in S is v : • Then Lorentz transformations are: • Lorentz transformations can be written in a matrix form Hendrik Antoon Lorentz (1853 – 1928)

Lorentz transformations 7. 2

Lorentz transformations • If the reference frame S‘ moves parallel to the x axis of the reference frame S: • If two events happen at the same location in S: • Time dilation 7. 2

Lorentz transformations • If the reference frame S‘ moves parallel to the x axis of the reference frame S: • If two events happen at the same time in S: • Length contraction 7. 2

Velocity addition • If the reference frame S‘ moves parallel to the x axis of the reference frame S: • If the reference frame S‘‘ moves parallel to the x axis of the reference frame S‘: 7. 3

Velocity addition 7. 3 • The Lorentz transformation from the reference frame S to the reference frame S‘‘: • On the other hand:

Four-velocity 7. 4 • Proper time is time measured in the system where the clock is at rest • For an object moving relative to a laboratory system, we define a contravariant vector of four-velocity:

Four-velocity • Magnitude of four-velocity 7. 4

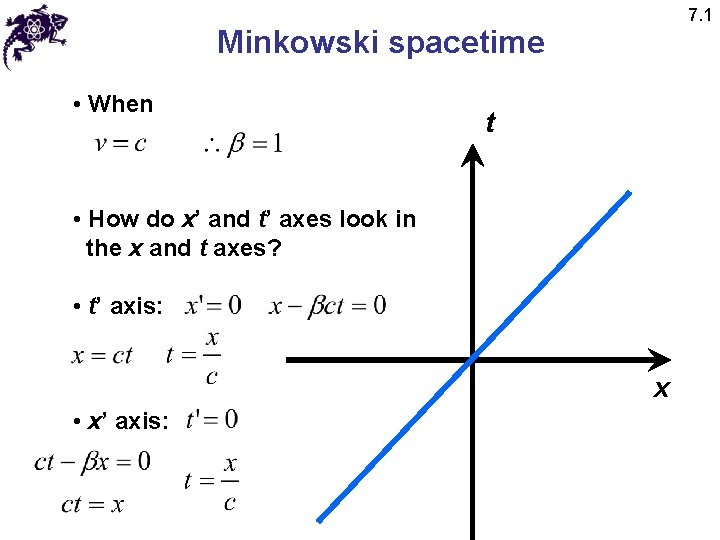
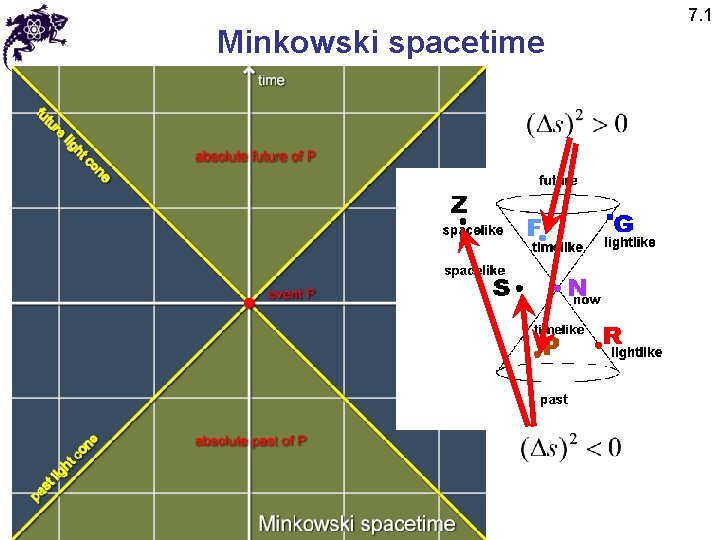
7. 1 Minkowski spacetime • Lorentz transformations for parallel axes: t t’ • How do x’ and t’ axes look in the x and t axes? Hermann Minkowski (1864 - 1909) x’ • t’ axis: x • x’ axis:

7. 1 Minkowski spacetime • When t • How do x’ and t’ axes look in the x and t axes? • t’ axis: x • x’ axis:

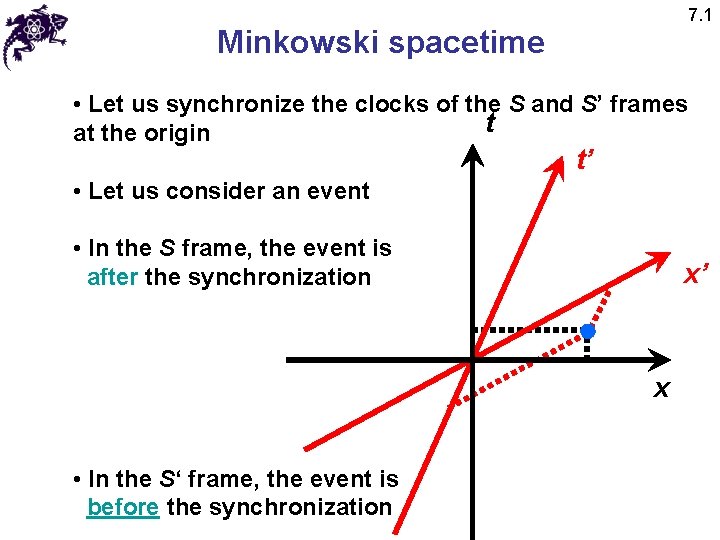
7. 1 Minkowski spacetime • Let us synchronize the clocks of the S and S’ frames t at the origin t’ • Let us consider an event • In the S frame, the event is to the right of the origin x’ x • In the S‘ frame, the event is to the left of the origin

7. 1 Minkowski spacetime • Let us synchronize the clocks of the S and S’ frames t at the origin t’ • Let us consider an event • In the S frame, the event is after the synchronization x’ x • In the S‘ frame, the event is before the synchronization

Minkowski spacetime 7. 1

Four-momentum 7. 4 • For an object moving relative to a laboratory system, we define a contravariant vector of four-momentum: • Magnitude of four-momentum

Four-momentum • Rest-mass: mass measured in the system where the object is at rest • For a moving object: • The equation has units of energy squared • If the object is at rest 7. 4

Four-momentum 7. 4

Four-momentum • Rest-mass energy: energy of a free object at rest – an essentially relativistic result • For slow objects: • For free relativistic objects, we introduce therefore the kinetic energy as 7. 4

Non-covariant Lagrangian formulation of relativistic mechanics • As a starting point, we will try to find a noncovariant Lagrangian formulation (the time variable is still separate) • The equations of motion should look like 7. 9

Non-covariant Lagrangian formulation of relativistic mechanics • For an electromagnetic potential, the Lagrangian is similar • The equations of motion should look like • Recall our derivations in “Lagrangian Formalism”: 7. 9

Non-covariant Lagrangian formulation of relativistic mechanics • Example: 1 D relativistic motion in a linear potential • The equations of motion: • Acceleration is hyperbolic, not parabolic 7. 9

Useful results

Non-covariant Hamiltonian formulation of relativistic mechanics • We start with a non-covariant Lagrangian: • Applying a standard procedure • Hamiltonian equals the total energy of the object 7. 9 8. 4

Non-covariant Hamiltonian formulation of relativistic mechanics • We have to express the Hamiltonian as a function of momenta and coordinates: 7. 9 8. 4

More on symmetries • Full time derivative of a Lagrangian: • Form the Euler-Lagrange equations: • If

Non-covariant Hamiltonian formulation of relativistic mechanics • Example: 1 D relativistic harmonic oscillator • The Lagrangian is not an explicit function of time • The quadrature involves elliptic integrals 7. 9 8. 4

Covariant Lagrangian formulation of relativistic mechanics: plan A 7. 10 • So far, our canonical formulations were not Lorentzinvariant – all the relationships were derived in a specific inertial reference frame • We have to incorporate the time variable as one of the coordinates of the spacetime • We need to introduce an invariant parameter, describing the progress of the system in configuration space: • Then

Covariant Lagrangian formulation of relativistic mechanics: plan A 7. 10 • Equations of motion • We need to find Lagrangians producing equations of motion for the observable behavior • First approach: use previously found Lagrangians and replace time and velocities according to the rule:

Covariant Lagrangian formulation of relativistic mechanics: plan A 7. 10 • Then • So, we can assume that • Attention: regardless of the functional dependence, the new Lagrangian is a homogeneous function of the generalized velocities in the first degree:

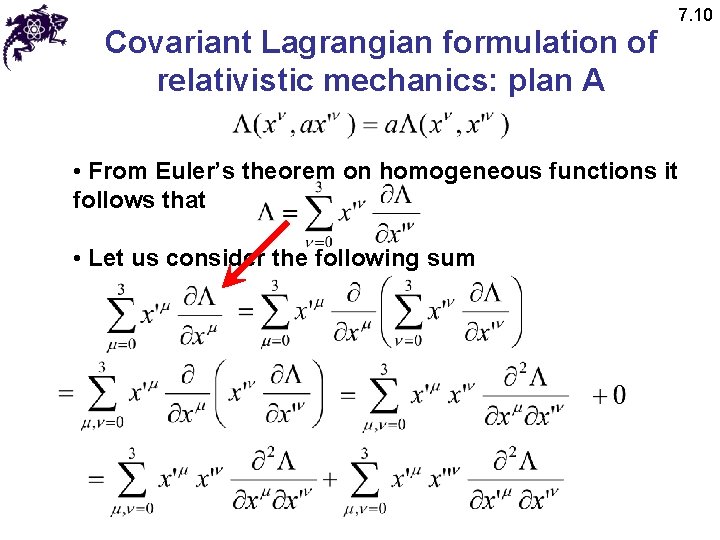
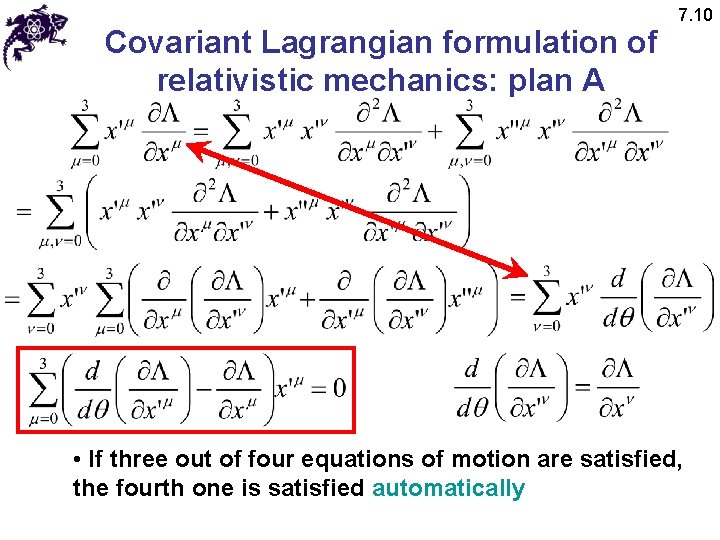
Covariant Lagrangian formulation of relativistic mechanics: plan A 7. 10 • From Euler’s theorem on homogeneous functions it follows that • Let us consider the following sum

Covariant Lagrangian formulation of relativistic mechanics: plan A 7. 10 • If three out of four equations of motion are satisfied, the fourth one is satisfied automatically

Example: a free particle • We start with a non-covariant Lagrangian 7. 10

Example: a free particle • Equations of motion 7. 10

Example: a free particle • Equations of motion of a free relativistic particle 7. 10

Covariant Lagrangian formulation of relativistic mechanics: plan B • Instead of an arbitrary invariant parameter, we can use proper time • However • Thus, components of the four-velocity are not independent: they belong to three-dimensional manifold (hypersphere) in a 4 D space • Therefore, such Lagrangian formulation has an inherent constraint • We will impose this constraint only after obtaining the equations of motion 7. 10

Covariant Lagrangian formulation of relativistic mechanics: plan B • In this case, the equations of motion will look like • But now the Lagrangian does not have to be a homogeneous function to the first degree • Thus, we obtain freedom of choosing Lagrangians from a much broader class of functions that produce Lorentz-invariant equations of motion • E. g. , for a free particle we could choose 7. 10

Covariant Lagrangian formulation of relativistic mechanics: plan B 7. 10 • If the particle is not free, then interaction terms have to be added to the Lagrangian – these terms must generate Lorentz-invariant equations of motion • In general, these additional terms will represent interaction of a particle with some external field • The specific form of the interaction will depend on the covariant formulation of the field theory • Such program has been carried out for the following fields: electromagnetic, strong/weak nuclear, and a weak gravitational

Covariant Lagrangian formulation of relativistic mechanics: plan B 7. 10 • Example: 1 D relativistic motion in a linear potential • In a specific inertial frame, the non-covariant Lagrangian was earlier shown to be • The covariant form of this problem is • In a specific inertial frame, the interaction vector will be reduced to

Example: relativistic particle in an electromagnetic field • For an electromagnetic field, the covariant Lagrangian has the following form: • The corresponding equations of motion: 7. 10 7. 6

Example: relativistic particle in an electromagnetic field • Maxwell's equations follow from this covariant formulation (check with your E&M class) 7. 10 7. 6

Covariant Lagrangian formulation of relativistic mechanics: plan B 7. 10 • What if we have many interacting particles? • Complication #1: How to find an invariant parameter describing the evolution? (If proper time, then of what object? ) • Complication #2: How to describe covariantly the interaction between the particles? (Information cannot propagate faster than a speed of light – action -at-a-distance is outlawed) • Currently, those are the areas of vigorous research

Covariant Hamiltonian formulation of relativistic mechanics: plan A 8. 4 • In ‘Plan A’, Lagrangians are homogeneous functions of the generalized velocities in the first degree • Let us try to construct the Hamiltonians using canonical approach (Legendre transformation) • ‘Plan A’: a bad idea !!!

Covariant Hamiltonian formulation of relativistic mechanics: plan B • In ‘Plan B’: instead of an arbitrary invariant parameter, we use proper time • We have to express four-velocities in terms of conjugate momenta and substitute these expressions into the Hamiltonian to make it a function of fourcoordinates and four-momenta • Don’t forget about the constraint: 8. 4

Covariant Hamiltonian formulation of relativistic mechanics: plan B • For a free particle: 8. 4

Covariant Hamiltonian formulation of relativistic mechanics: plan B • For a particle in an electromagnetic field: 8. 4

Relativistic angular momentum • For a single particle, the relativistic angular momentum is defined as an antisymmetric tensor of rank 2 in Minkowski space: • This tensor has 6 independent elements; 3 of them coincide with the components of a regular angular momentum vector in non-relativistic limit 7. 8

Relativistic angular momentum • Evolution of the relativistic angular momentum is determined by: From the equations of motion • For open systems, we have to define generalized relativistic torques in a covariant form 7. 8

Relativistic kinematics of collisions • The subject of relativistic collisions is of considerable interest in experimental high-energy physics • Les us assume that the colliding particle do not interact outside of the collision region, and are not affected by any external potentials and fields • We choose to work in a certain inertial reference frame; in the absence of external fields, the fourmomentum of the system is conserved • Conservation of a four-momentum includes conservation of a linear momentum and conservation of energy 7. 7

Relativistic kinematics of collisions • Usually we know the four-momenta of the colliding particles and need to find the four-momenta of the collision products • There is a neat trick to deal with such problems: • 1) Rearrange the equation for the conservation of the four-momentum of the system so that the fourmomentum for the particle we are not interested in stands alone on one side of the equation • 2) Write the magnitude squared of each side of the equation using the result that the magnitude squared of a four-momentum is an invariant 7. 7

Relativistic kinematics of collisions • Let us assume that we have two particles before the collision (A and B) and two particles after the collision (C and D) • Conservation of the four-momentum of the system: • 1) Rearrange the equation (supposed we are not interested in particle D) • 2) Magnitude squared of each side of the equation: 7. 7

Relativistic kinematics of collisions 7. 7

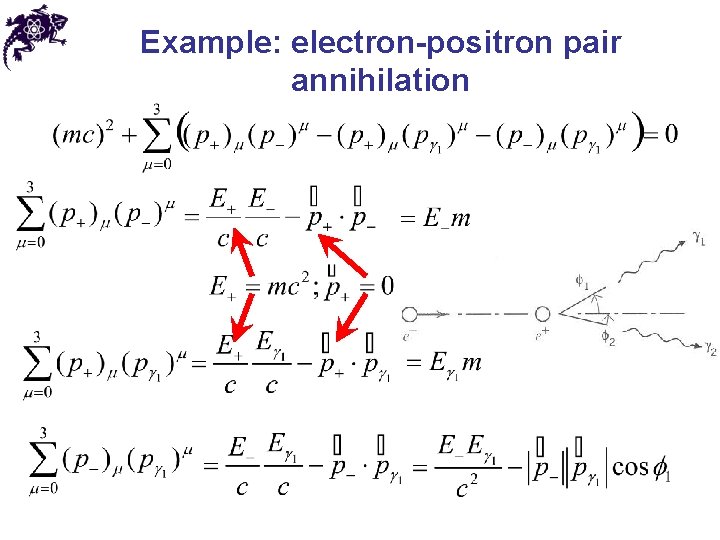
Example: electron-positron pair annihilation • Annihilation of an electron and a positron produces two photons • Conservation of the four-momentum of the system: • Let us assume that the positron is initially at rest: • 1) Rearrange the equation

Example: electron-positron pair annihilation • 2) Magnitude squared of each side of the equation:

Example: electron-positron pair annihilation

Example: electron-positron pair annihilation • The photon energy will be at a maximum when emitted in the forward direction, and at a minimum when emitted in the backward direction
 Modern physics vs classical physics
Modern physics vs classical physics Acetylcholine crisis
Acetylcholine crisis Relativistic circular motion
Relativistic circular motion Relativistic thinking example
Relativistic thinking example Length contraction
Length contraction Al's relativistic adventures
Al's relativistic adventures General relativity equation
General relativity equation Relativistic momentum
Relativistic momentum Relativistic thinking example
Relativistic thinking example Relativistic mass formula
Relativistic mass formula Cognitive changes in early adulthood
Cognitive changes in early adulthood Relativistic kinetic energy
Relativistic kinetic energy Kinetic energy of a relativistic particle
Kinetic energy of a relativistic particle Relativity
Relativity Relative speed of approach
Relative speed of approach Clairaut equation
Clairaut equation A physical education chapter 28
A physical education chapter 28 Physical development in adulthood
Physical development in adulthood Relativistic mean field theory
Relativistic mean field theory Doppler effect animation ppt
Doppler effect animation ppt Relativistic momentum
Relativistic momentum Virial theorem in classical mechanics
Virial theorem in classical mechanics Virial theorem in classical mechanics
Virial theorem in classical mechanics Define angular momentum
Define angular momentum Classical mechanics
Classical mechanics Classical mechanics
Classical mechanics Classical mechanics
Classical mechanics Classical mechanics
Classical mechanics Classical mechanics
Classical mechanics Classical mechanics equations
Classical mechanics equations Classical mechanics
Classical mechanics Physics 111 lecture notes
Physics 111 lecture notes Perturbation theory classical mechanics
Perturbation theory classical mechanics Classical mechanics
Classical mechanics Ap quantum physics
Ap quantum physics Ncea level 2 physics mechanics 2013 answers
Ncea level 2 physics mechanics 2013 answers Quantum physics vs quantum mechanics
Quantum physics vs quantum mechanics Physics ia topic ideas
Physics ia topic ideas Holt physics chapter 8 fluid mechanics test answers
Holt physics chapter 8 fluid mechanics test answers Fluid mechanics
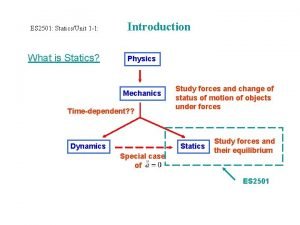
Fluid mechanics What is statics
What is statics Classical physics
Classical physics Classical physics
Classical physics Failures of classical physics
Failures of classical physics Pixabay
Pixabay Oppenheim
Oppenheim Adam smith
Adam smith Turkistonda rus maktablarining ochilishi
Turkistonda rus maktablarining ochilishi Novelas realistas del siglo xix
Novelas realistas del siglo xix Frankenstein ch 18 summary
Frankenstein ch 18 summary Siglo xix contexto social
Siglo xix contexto social Contexto historico social y cultural del romanticismo
Contexto historico social y cultural del romanticismo Narrativa del siglo xix
Narrativa del siglo xix Principales caracteristicas del imperialismo
Principales caracteristicas del imperialismo Site:slidetodoc.com
Site:slidetodoc.com F em algarismo romano
F em algarismo romano Xix movimiento literario
Xix movimiento literario Literatura siglo xviii
Literatura siglo xviii Xix movimiento literario
Xix movimiento literario Rebeliones criollas del siglo xix
Rebeliones criollas del siglo xix Sztuka baroku cechy
Sztuka baroku cechy Pendores
Pendores Xix domingo del tiempo ordinario
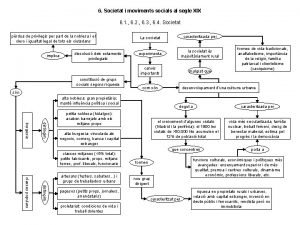
Xix domingo del tiempo ordinario Societat i moviments socials del segle xix
Societat i moviments socials del segle xix Xix domenica del tempo ordinario anno b
Xix domenica del tempo ordinario anno b Xix
Xix