Clase prctica Programacin Lineal El proceso de identificacin

Clase práctica Programación Lineal

El proceso de identificación del Lote óptimo de producción, requiere de las siguientes etapas: Pasos 1. 2. 3. 4. 5. Plantear la Función Objetivo Identificar las restricciones. Plantear las restricciones como inecuaciones. Convertir las inecuaciones en ecuaciones Identificar los puntos necesarios para graficar el sistema de inecuaciones. 6. Graficar todas las rectas 7. Identificar la región de factibilidad 8. Calcular los puntos que forman sus vértices. 9. Reemplazar los puntos calculados en el punto anterior en la Función Objetivo y ver cual cumple de mejor manera con el objetivo (máx o min. ) 10. Interpretar el resultado.

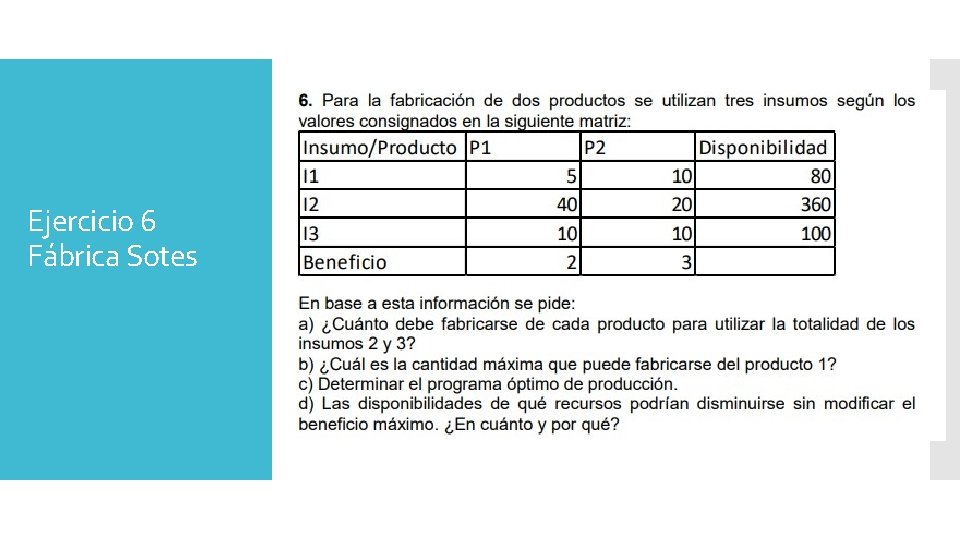
Ejercicio 6 Fábrica Sotes

Función Objetivo: Z = 2. P 1+3. P 2 Solución Restricciones: Insumo 1= 5. P 1+10. P 2 = 80 Insumo 2= 40. P 1+20 P 2 =360 Insumo 3= 10. P 1+10. P 2 =100

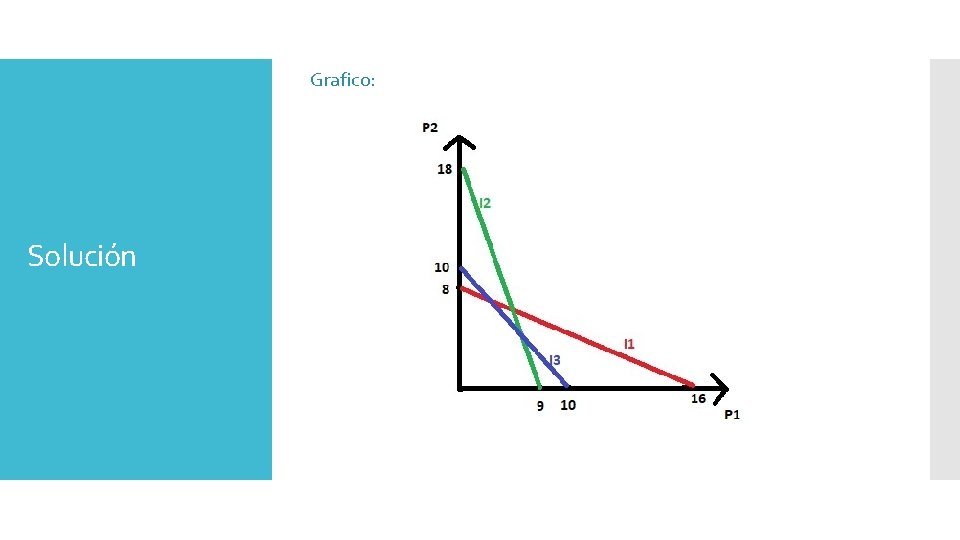
Puntos necesarios para graficar las rectas: Insumo 1= 5. P 1+10. P 2 = 80 Si reemplazamos P 1=0; obtenemos P 2 =8 Si reemplazamos P 2=0, obtenemos P 1= 16. Entonces los puntos (0; 8) y (16; 0) nos permiten graficar esta recta. Insumo 2= Solución 40. P 1+20 P 2 =360 Si reemplazamos P 1=0; obtenemos P 2 =18 Si reemplazamos P 2=0, obtenemos P 1= 9 Entonces los puntos (0; 18) y (9; 0) nos permiten graficar esta recta. Insumo 3= 10. P 1+10. P 2 =100 Si reemplazamos P 1=0; obtenemos P 2 =10 Si reemplazamos P 2=0, obtenemos P 1= 10. Entonces los puntos (0; 10) y (10; 0) nos permiten graficar esta recta.

Grafico: Solución

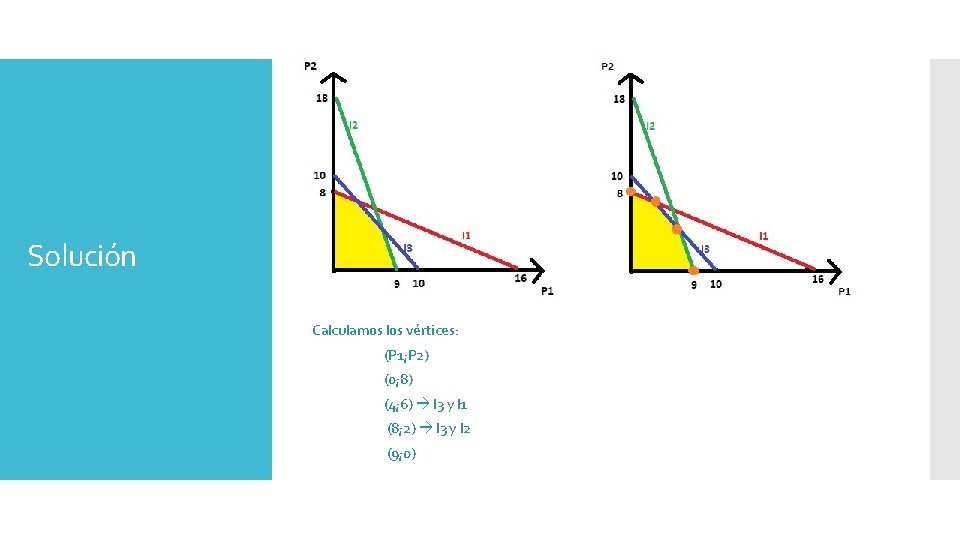
Solución Calculamos los vértices: (P 1; P 2) (0; 8) (4; 6) I 3 y I 1 (8; 2) I 3 y I 2 (9; 0)

Igualo las rectas que se cruzan para obtener las intersecciones: Insumo 1= 5. P 1+10. P 2 = 80 P 1= (80 -10. P 2)/5 Insumo 3= 10. P 1+10. P 2 =100 P 1= (100 -10. P 2)/10 (80 -10. P 2)/5=(100 -10. P 2)/10 Solución P 2= 6 P 1= 4 Insumo 2= 40. P 1+20 P 2 =360 P 1= (360 -20. P 2)/40 Insumo 3= 10. P 1+10. P 2 =100 P 1= (100 -10. P 2)/10 (360 -20. P 2)/40=(100 -10. P 2)/10 P 2=2 P 1=8

Reemplazo los puntos hallados en la función objetivo: Z= 2. P 1+3. P 2 (P 1; P 2) Solución (0; 8) Z= 24 (4; 6) Z= 26 (8; 2) Z= 22 (9; 0) Z= 18

Una confitería es famosa por sus dos especialidades de tartas: la tarta de chocolate y la de frutillas con crema. La de chocolate requiere para su elaboración medio kilo de azúcar y 8 huevos, y tiene una ganancia de $100 por unidad vendida. La tarta de frutillas necesita un kilo de azúcar y 8 huevos, y tiene un beneficio de $120 por unidad vendida. Ejercicio modelo prueba En el almacén les quedan 10 kilos de azúcar y 120 huevos. Considerando los inventarios de previsión y de seguridad, el dueño de la confitería definió no hacer más de 12 tartas de chocolate por día. Determinar: 1) ¿Cuántas unidades de cada producto se pueden producir para obtener el mayor ingreso? 2) Considerando las cantidades óptimas a producir, ¿se puede reducir algún inventario de materias primas? ¿Cuál y en cuántas unidades? 3) ¿Cuánto se puede producir como máximo de las tartas de chocolate?

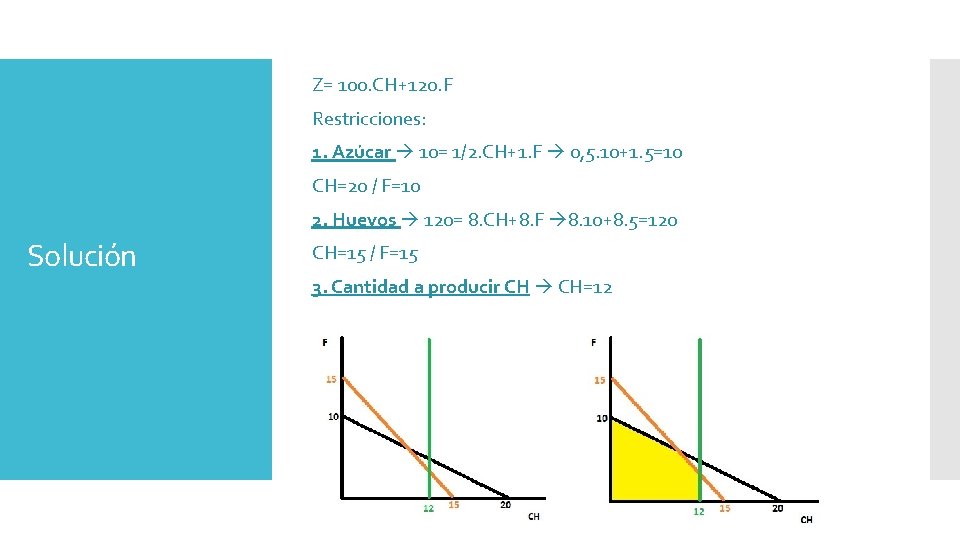
Z= 100. CH+120. F Restricciones: 1. Azúcar 10= 1/2. CH+1. F 0, 5. 10+1. 5=10 CH=20 / F=10 2. Huevos 120= 8. CH+8. F 8. 10+8. 5=120 Solución CH=15 / F=15 3. Cantidad a producir CH CH=12

Reemplazo los puntos hallados en la función objetivo: Z= 100. CH+120. F (F; CH) Solución (10; 0) Z= 1200 (5; 10) Z= 1600 (3; 12) Z= 1560 (0; 12) Z= 1200