Chapter 8 Fundamental Sampling Distributions and Data Descriptions

Chapter 8: Fundamental Sampling Distributions and Data Descriptions q Introduction to random sampling and statistical inference q Populations and samples q Sampling distribution of means Ø Central Limit Theorem q Other distributions Ø S 2 Ø t-distribution Ø F-distribution EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 1

Populations and Samples q Population: “a group of individual persons, objects, or items from which samples are taken for statistical measurement” 1 q Sample: “a finite part of a statistical population whose properties are studied to gain information about the whole” 1 q Population – the totality of the observations with which we are concerned 2 q Sample – a subset of the population 2 1 (Merriam-Webster Online Dictionary, http: //www. m-w. com/, October 5, 2004) 2 Walpole, Myers, and Ye (2007) Probability and Statistics for Engineers and Scientists EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 2

Examples Population Students pursuing undergraduate engineering degrees Sample 1000 engineering students selected at random from all engineering programs in the US Cars capable of speeds in 50 cars selected at excess of 160 mph. random from among those certified as having achieved 160 mph or more during 2003 EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 3

More Examples Population Sample Potato chips produced at the Frito-Lay plant in Kathleen 10 chips selected at random every 5 minutes as the conveyor passes the inspector Freshwater lakes and rivers 4 samples taken from randomly selected locations in randomly selected and representative freshwater lakes and rivers EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 4

Basic Statistics (review) Sample Mean: A class project involved the formation of three 10 -person teams (Team Q, Team R and Team S). At the end of the project, team members were asked to give themselves and each other a grade on their contribution to the group. A random sample from two of the teams yielded the following results: Q R = 87. 5 92 85 95 88 85 75 78 92 EGR 252 - Ch. 8 9 th edition = 85. 0 JMB 2018 2019 Slide 5

Basic Statistics (review) q Sample variance equation: q For our example: Q team sample R team sample 92 85 95 88 85 75 78 92 Ø Calculate the sample standard deviation (s) for each sample. Ø SQteam = 7. 59386 and SRteam = 7. 25718 EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 6

Sampling Distributions q If we conduct the same experiment several times with the sample size, the probability distribution of the resulting statistic is called a sampling distribution q Sampling distribution of the mean: if n observations are taken from a normal population with mean μ and variance σ2, then: EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 7

Central Limit Theorem q Given: X : the mean of a random sample of size n taken from a population with mean μ and finite variance σ2, the limiting form of the distribution of is the standard normal distribution n(z; 0, 1) Note that this equation for Z applies when we have sample data. Compare to the Z equation for the population (Ch 6). EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 8

Central Limit Theorem-Distribution of X q If the population is known to be normal, the sampling distribution of X will follow a normal distribution. q Even when the distribution of the population is not normal, the sampling distribution of X is normal when n is large. Ø NOTE: when n is not large, we cannot assume the distribution of X is normal. EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 9

Sampling Distribution of the Difference Between Two Averages q Given: Ø Two samples of size n 1 and n 2 are taken from two populations with means μ 1 and μ 2 and variances σ12 and σ22 q Then, EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 10

Sampling Distribution of S 2 q Given: Ø If S 2 is the variance of of a random sample of size n taken from a population with mean μ and finite variance σ2, q Then, has a χ 2 distribution with ν = n - 1 EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 11
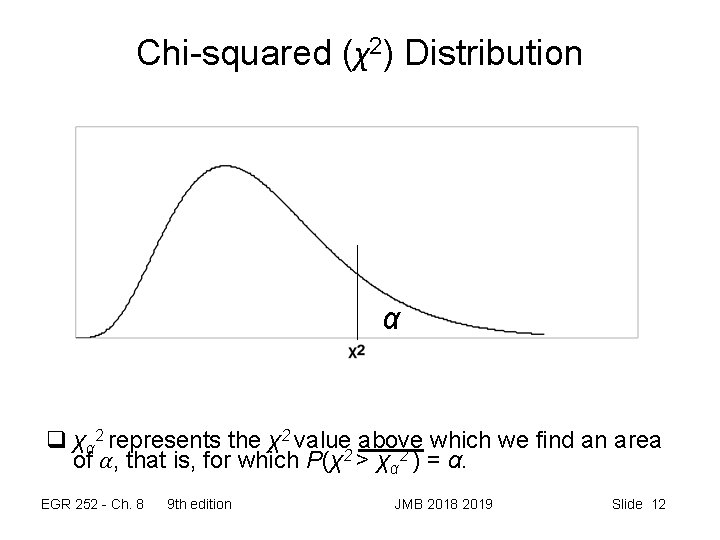
Chi-squared (χ2) Distribution α q χα 2 represents the χ2 value above which we find an area of α, that is, for which P(χ2 > χα 2 ) = α. EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 12

Example q Look at example 8. 7, pg. 245: A manufacturer of car batteries guarantees that his batteries will last, on average, 3 years with a standard deviation of 1 year. A sample of five of the batteries yielded a sample variance of 0. 815. Does the manufacturer have reason to suspect the standard deviation is no longer 1 year? μ = 3 σ = 1 n = 5 Degrees of freedom (v) = n-1 s 2 = 0. 815 If the χ2 value fits within an interval that covers 95% of the χ2 values with 4 degrees of freedom, then the estimate for σ is reasonable. See Table A. 5, (pp. 739 -740) For alpha = 0. 025, Χ 2 =11. 143 The Χ 2 value for alpha = 0. 975 is 0. 484. EGR 252 - Ch. 8 9 th edition 0. 484 3. 26 JMB 2018 2019 11. 143 Slide 13
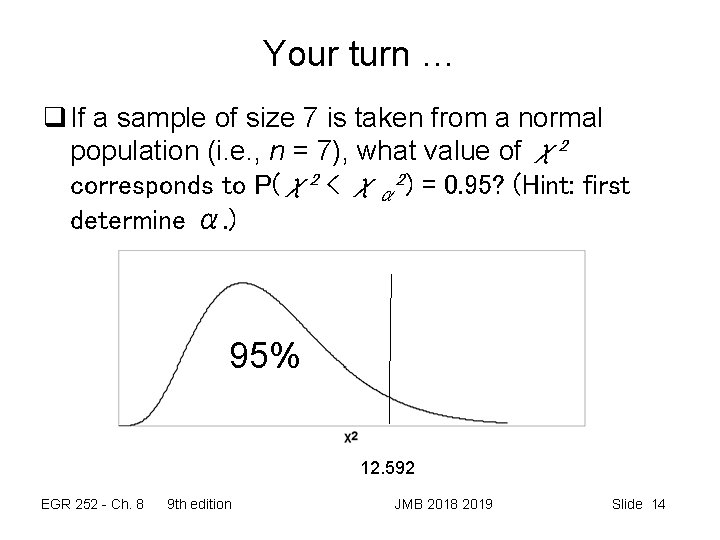
Your turn … q If a sample of size 7 is taken from a normal population (i. e. , n = 7), what value of χ2 corresponds to P(χ2 < χα 2) = 0. 95? (Hint: first determine α. ) 95% 12. 592 EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 14

t- Distribution q Recall, by Central Limit Theorem: is n(z; 0, 1) q Assumption: σ known (Z ) (Generally, if an engineer is concerned with a familiar process or system, this is reasonable, but …) EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 15

What if we don’t know σ? (sigma unknown) q New statistic: Where, and follows a t-distribution with ν = n – 1 degrees of freedom. EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 16

Characteristics of the t-Distribution q Look at Figure 8. 8, pg. 248 q Note: Ø Shape: _____________ Ø Effect of ν: _____________ q See table A. 4, pp. 737 -738 Note that the table yields the right tail of the distribution. EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 17

F-Distribution q Given: Ø S 12 and S 22, the variances of independent random samples of size n 1 and n 2 taken from normal populations with variances σ12 and σ22, respectively, q Then, has an F-distribution with ν 1 = n 1 - 1 and ν 2 = n 2 – 1 degrees of freedom. (See table A. 6, pp. 741 -744) EGR 252 - Ch. 8 9 th edition JMB 2018 2019 Slide 18
- Slides: 18