CHAPTER 5 The Schrodinger Eqn 5 1 5

CHAPTER 5 The Schrodinger Eqn. 5. 1 5. 2 5. 3 5. 4 5. 5 The Schrödinger Wave Equation Expectation Values Infinite Square-Well Potential Finite Square-Well Potential Three-Dimensional Infinite. Potential Well 5. 6 Simple Harmonic Oscillator 5. 7 Barriers and Tunneling Homework due Wednesday Oct. Read Chapters 4 and 5 of Kane Chapter 4: 2, 3, 5, 13, 20 Chapter 5: 3, 4, 5, 7, 8 First exam this Friday in class 1 st Erwin Schrödinger (1887 -1961)

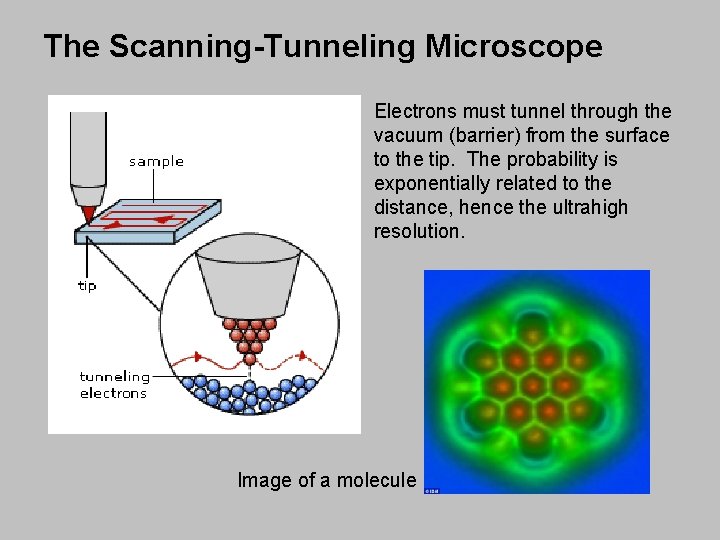
The Scanning-Tunneling Microscope Electrons must tunnel through the vacuum (barrier) from the surface to the tip. The probability is exponentially related to the distance, hence the ultrahigh resolution. Image of a molecule

Alpha-Particle Decay Tunneling explains alpha-particle decay of heavy, radioactive nuclei. Outside the nucleus, the Coulomb force dominates. Inside the nucleus, the strong, short-range attractive nuclear force dominates the repulsive Coulomb force. The potential is ~ a square well. The potential barrier at the nuclear radius is several times greater than the energy of an alpha particle. In quantum mechanics, however, the alpha particle can tunnel through the barrier. This is radioactive decay!

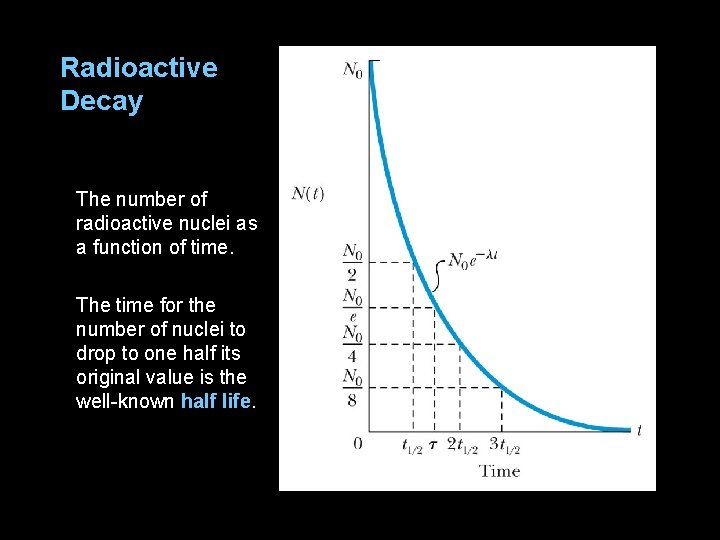
Radioactive Decay The number of radioactive nuclei as a function of time. The time for the number of nuclei to drop to one half its original value is the well-known half life.

Three-Dimensional Infinite. Potential Well y The wave function must be a function of all three spatial coordinates. z So consider momentum as an operator in three dimensions: The three-dimensional Schrödinger wave equation is: or: x

The 3 D infinite potential well It’s easy to show that: where: and: Lz When the box is a cube: y Ly z x Lx

Degeneracy Try 10, 4, 3 and 8, 6, 5 Note that more than one wave function can have the same energy. When more than one wave function has the same energy, those quantum states are said to be degenerate. Degeneracy results from symmetries of the potential energy function that describes the system. A perturbation of the potential energy can remove the degeneracy. Examples of perturbations include external electric or magnetic fields or various internal effects, like the magnetic fields due to the spins of the various particles.

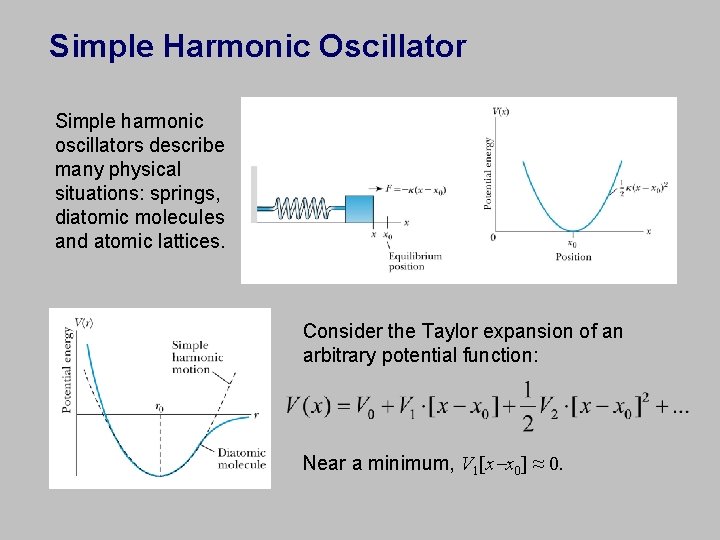
Simple Harmonic Oscillator Simple harmonic oscillators describe many physical situations: springs, diatomic molecules and atomic lattices. Consider the Taylor expansion of an arbitrary potential function: Near a minimum, V 1[x-x 0] ≈ 0.

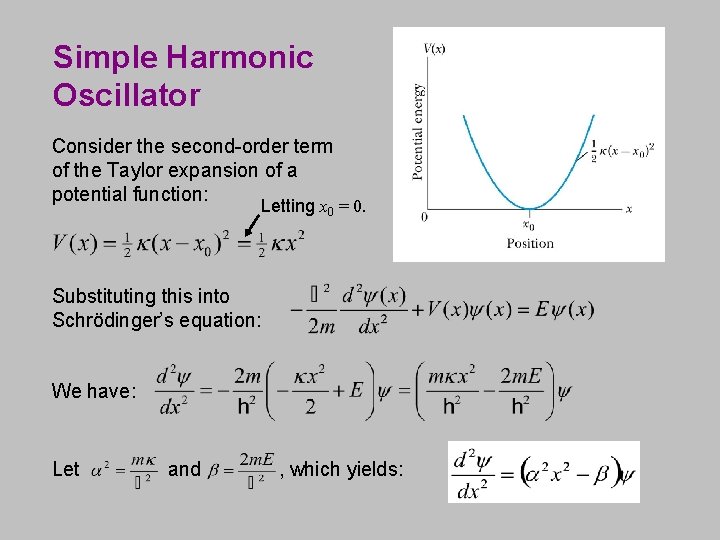
Simple Harmonic Oscillator Consider the second-order term of the Taylor expansion of a potential function: Letting x 0 = 0. Substituting this into Schrödinger’s equation: We have: Let and , which yields:

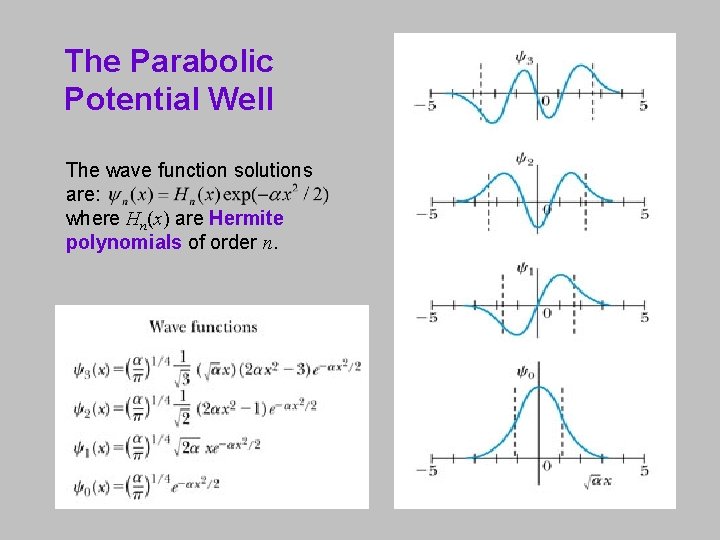
The Parabolic Potential Well The wave function solutions are: where Hn(x) are Hermite polynomials of order n.

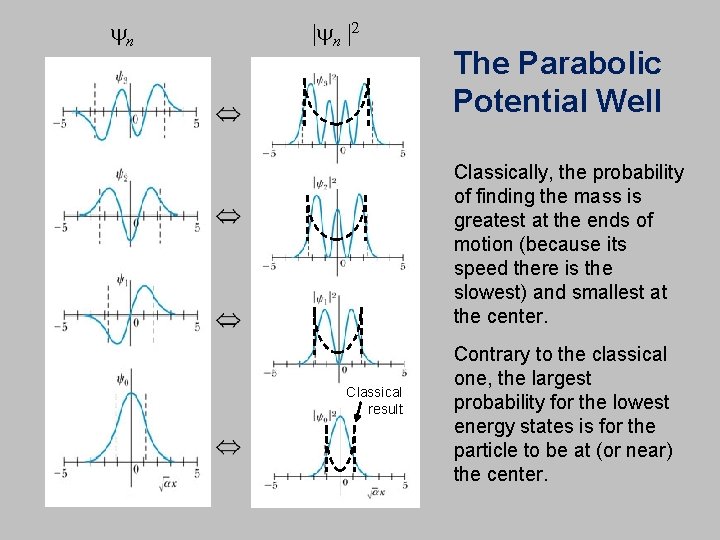
yn |2 The Parabolic Potential Well Classically, the probability of finding the mass is greatest at the ends of motion (because its speed there is the slowest) and smallest at the center. Classical result Contrary to the classical one, the largest probability for the lowest energy states is for the particle to be at (or near) the center.

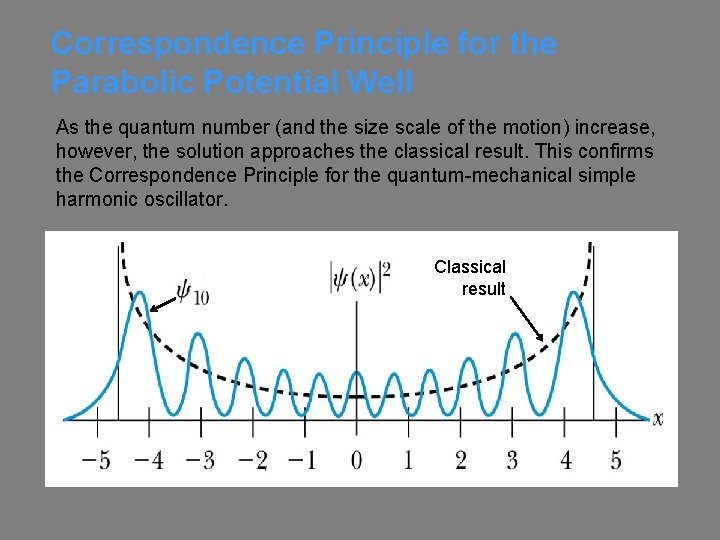
Correspondence Principle for the Parabolic Potential Well As the quantum number (and the size scale of the motion) increase, however, the solution approaches the classical result. This confirms the Correspondence Principle for the quantum-mechanical simple harmonic oscillator. Classical result

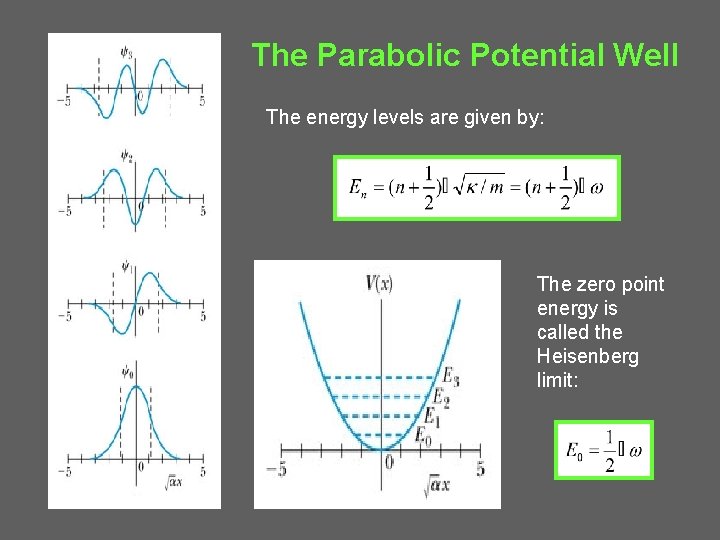
The Parabolic Potential Well The energy levels are given by: The zero point energy is called the Heisenberg limit: