Chapter 11 Minimum Cost Flows Network Simplex Algorithms








- Slides: 10

Chapter 11 Minimum Cost Flows: Network Simplex Algorithms 1

Network Simplex Algorithm q Streamlined implementation of the bounded variable simplex method on the network. (See Application 9. 6 for an application of the minimum cost flow problem. ) q Formulation: N is n m matrix min cx s. t. Nx = b 0 x u Optimality conditions of the bounded variable simplex method: Let denote the dual variable associated with the mass balance constraints. Nij: a column of N corresponding to arc (i, j) = ei – ej reduced cost cij = cij – ( (i) - (j)) = cij - (i) + (j) cij. Network Theory and Applications 2010 2

For nonbasic variables: If cij 0 xij = 0 If cij 0 xij = uij For basic variables: cij = 0 q The set of basic variables corresponds to a spanning tree in the network. How to represent the spanning tree and perform operations on the spanning tree? Use three arrays pred(i), depth(i), and thread(i) to represent a spanning tree. Network Theory and Applications 2010 3

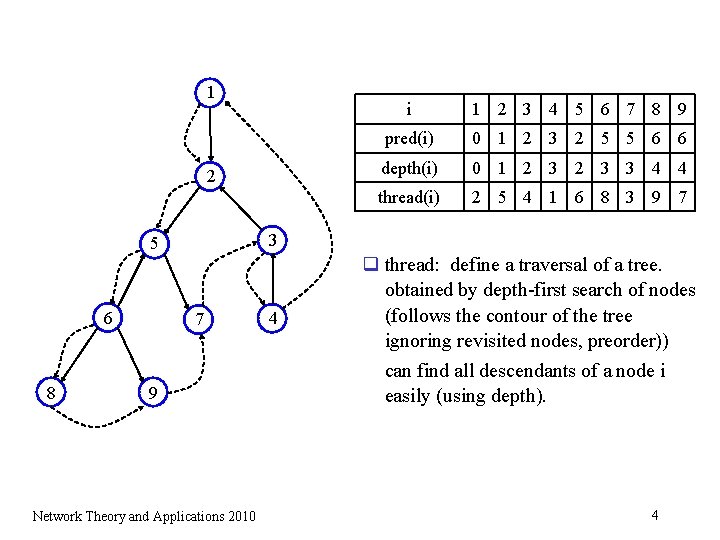
1 2 8 1 2 3 4 5 6 7 8 9 pred(i) 0 1 2 3 2 5 5 6 6 depth(i) 0 1 2 3 3 4 4 thread(i) 2 5 4 1 6 8 3 9 7 3 5 6 i 7 9 Network Theory and Applications 2010 4 q thread: define a traversal of a tree. obtained by depth-first search of nodes (follows the contour of the tree ignoring revisited nodes, preorder)) can find all descendants of a node i easily (using depth). 4

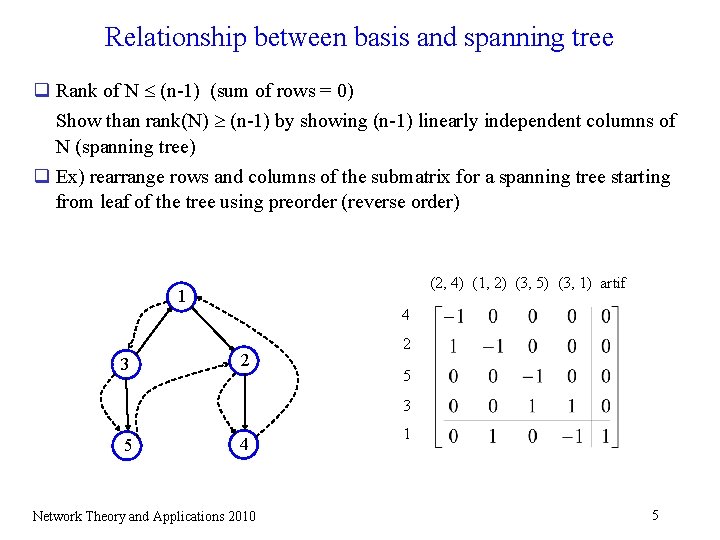
Relationship between basis and spanning tree q Rank of N (n-1) (sum of rows = 0) Show than rank(N) (n-1) by showing (n-1) linearly independent columns of N (spanning tree) q Ex) rearrange rows and columns of the submatrix for a spanning tree starting from leaf of the tree using preorder (reverse order) (2, 4) (1, 2) (3, 5) (3, 1) artif 1 3 4 2 2 5 3 5 4 Network Theory and Applications 2010 1 5

q Converse) (n-1) linearly independent columns of N spanning tree Pf) Suppose not a spanning tree, then there exists a cycle W. Take (i, j) W( 1)Nij = (i, j) W( 1)(e(i) – e(j)) = 0. (Use +1 forward arc, -1 for backward arc in W. ) Hence the columns are linear dependent. � q Thm) (n-1) linearly independent columns of N spanning tree. q 2 approaches: Ø Drop one constraint Ø Add an artificial variable to a row of N (take the node as root of the tree) (can take the dual value (r) = 0 for the root node from B = c. B for basis B) Network Theory and Applications 2010 6

q LP operations: Computing basic feasible solution and dual solution : x. B : Bx. B = b – Lx. L – Ux. U, B: lower triangular Bx. B = b’, solve by substitution (on network, determine flows starting from leaf nodes) : B = c. B, solve by substitution (on network, determine starting from root node using cij - (i) + (j) = 0 ) Actually, x and are updated, rather than computed again from scratch. Finding an entering nonbasic variable: Ø cij < 0 and xij = 0 (xij < uij): want to increase flow on arc (i, j) Ø cij > 0 and xij = uij (xij > 0): want to decrease flow on arc (i, j) Leaving basic variable: Have x. B = B-1 b – B-1 Lx. L – B-1 Ux. U Ø If increase entering xj (xj xj + t): x. B(t) = x. B* - td (d: updated column of xj) Ø If decrease entering xj (xj xj - t): x. B(t) = x. B* + td Ø determine largest t satisfying l. B x. B u. B Update solution Network Theory and Applications 2010 7

q Operations on the network: Computing : Ø set (1) = 0 (root) Ø Following thread(i) index, use cij - (i) + (j) = 0 i = pred(j) (i, j) A (j) = (i) – cij (j, i) A (j) = (i) + cij Computing x. B: Ø For (i, j) U, set xij = uij, b’(i) = b(i) – uij, b’(j) = b(j) + uij. Then determine tree arc flow starting from leaf node. if j is leaf node, (i, j) A xij = -b’(j), b’(i) – xij = b’(i) + b’(j) if j is leaf node, (j, i) A xij = b’(j), b’(i) + xij = b’(i) + b’(j) Read thread(i), and put them into a stack. Pop operation chooses leaf nodes always. Network Theory and Applications 2010 8

(continued) Finding initial tree: no details here Choosing an entering arc: some rules possible Determining leaving arc: Ø Suppose arc (k, l) entering creates a cycle W orientation of cycle: same as (k, l) if xkl = 0, opposite direction of (k, l) if xkl = uij. (want to increase flow along the cycle) ij = uij – xij, if (i, j) W and forward arc xij, if (i, j) W and backward arc = min{ ij: (i, j) W}. Augment units of flow on W. A blocking arc leaves tree. Ø In simplex method, x. B(t) = x. B* - td (increase case) d = B-1 Nkl or Bd = Nkl (Nkl + W( 1)Nij = 0, +1 forward, -1 for backward) choose dij = -1, if (i, j) is forward arc in W = +1, if (i, j) is backward arc in W = 0, otherwise is solution corresponds to flow augmentation on W. Network Theory and Applications 2010 9

(continued) Identifying the cycle: Ø Identify apex (join) of the cycle W. Use predecessor, depth index to identify apex. Also compute at the same time. Updating the tree: Ø No details here. Refer Chapter 19, Linear Programming, Vasek Chvatal, 1983. Ø Can use thread to update the representation of the tree easily. Network Theory and Applications 2010 10