10 4 Network Simplex Algorithm for Optimal Flows




















































- Slides: 73

10. 4 Network Simplex Algorithm for Optimal Flows q Opt Theory 2019 1

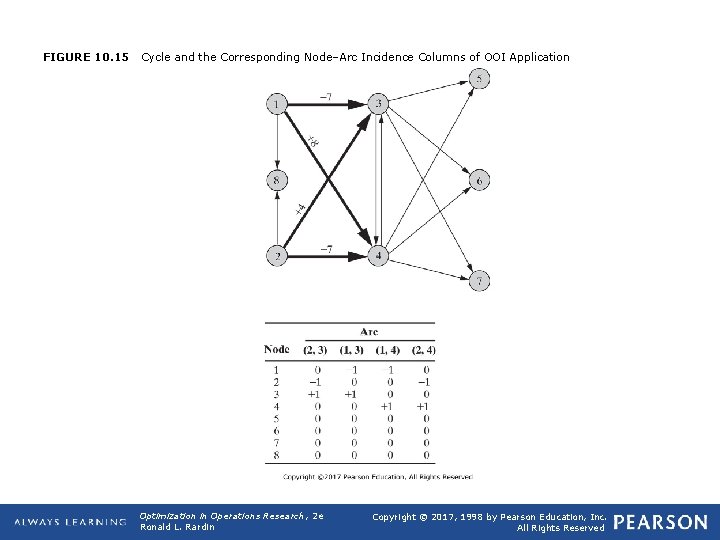
FIGURE 10. 15 Cycle and the Corresponding Node–Arc Incidence Columns of OOI Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 3

q Opt Theory 2019 4

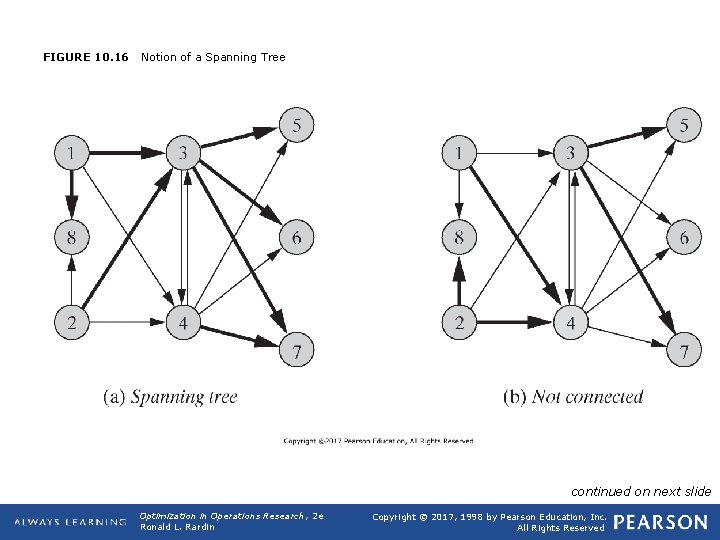
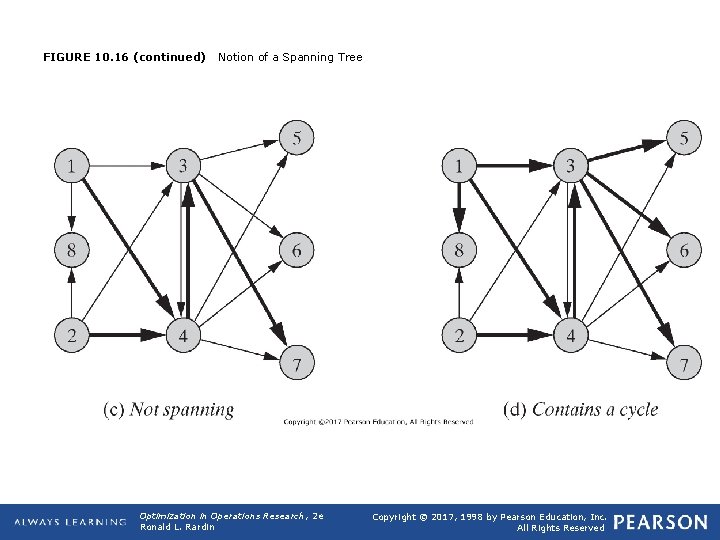
q Spanning Trees of Networks q We say that a graph is connected if there is a chain between every pair of nodes. A graph is a tree if it is connected and contains no cycles. A tree is a spanning tree if it touches every node of a graph. (forest if it contains no cycles) (same definitions for undirected cases too) q See Figure 10. 16 q Principle 10. 30: Every pair of nodes in a tree is connected by a unique chain of the tree. If the tree spans a graph, every pair of nodes in the graph is connected by a unique chain of the tree. q Note that a spanning tree always include a node connected by one arc (degree of the node is 1), which is called a leaf node. Opt Theory 2019 5

FIGURE 10. 16 Notion of a Spanning Tree continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

FIGURE 10. 16 (continued) Notion of a Spanning Tree Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 8

q Opt Theory 2019 9

q Opt Theory 2019 10

q Opt Theory 2019 11

q Opt Theory 2019 12

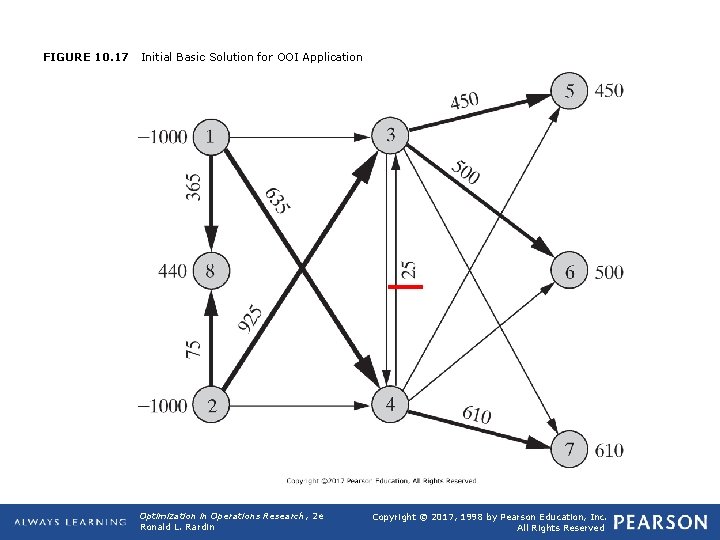
FIGURE 10. 17 Initial Basic Solution for OOI Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 14

q Opt Theory 2019 15

q Opt Theory 2019 16

q OR-Opt. 2019 17

q OR-Opt. 2019 18

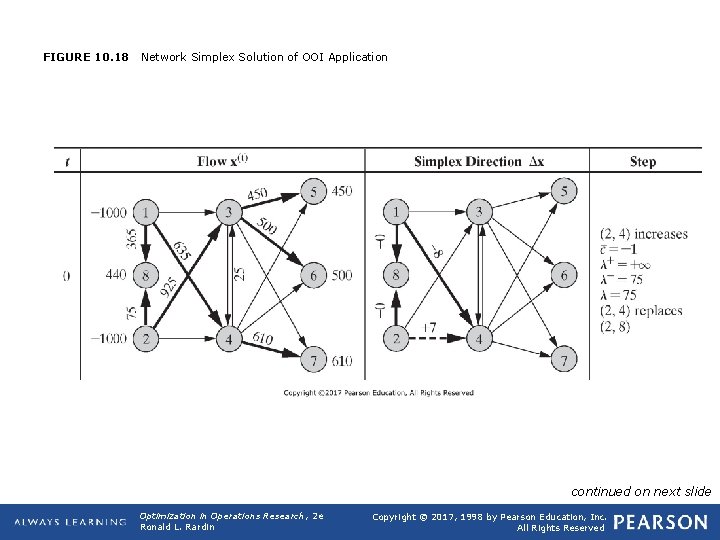
FIGURE 10. 18 Network Simplex Solution of OOI Application continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

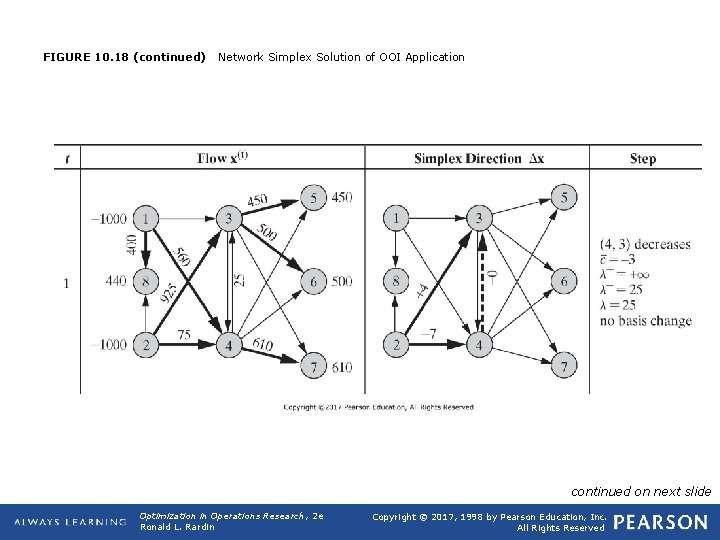
FIGURE 10. 18 (continued) Network Simplex Solution of OOI Application continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

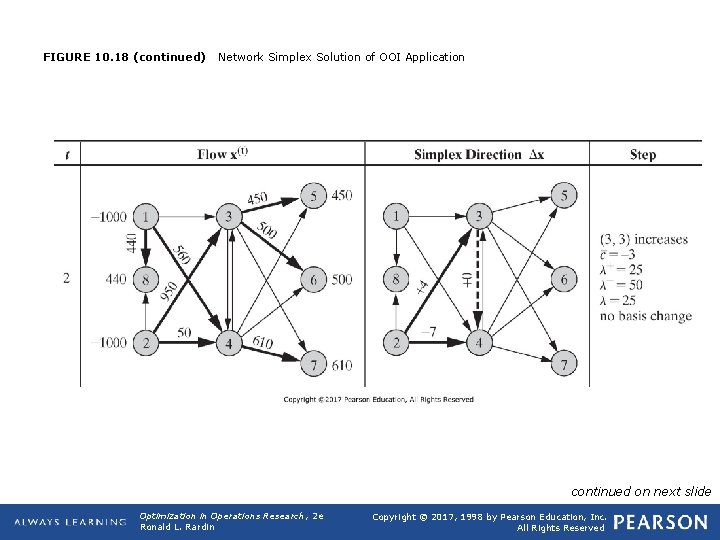
FIGURE 10. 18 (continued) Network Simplex Solution of OOI Application continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

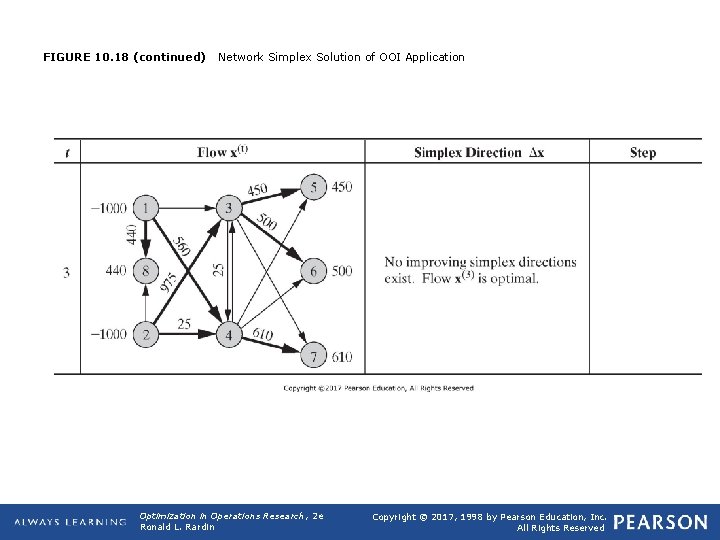
FIGURE 10. 18 (continued) Network Simplex Solution of OOI Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 23

q The procedure of the network simplex method are carried out on the graph. We need to maintain and update proper data structure to represent spanning trees. It’s beyond the scope of this class and we do not discuss it any further. q We also need to consider how we can avoid cycling in the network simplex iterations. Opt Theory 2019 24

10. 5 Integrality of Optimal Network Flows q Opt Theory 2019 25

q Opt Theory 2019 26

q Opt Theory 2019 27

10. 6 Transportation and Assignment Models q Opt Theory 2019 28

q Opt Theory 2019 29

q Opt Theory 2019 30

q There exist more difficult assignment problems (e. g. quadratic assignment problem, generalized assignment problem, …). We will consider them later in integer programming part. q Application 10. 4: CAM Assignment q Computer-aided manufacturing system. Automatically route jobs through workstations. Each job consists of a sequence of required machining and assembly operations. Each time that a job completes some operation, the system must select the next station to which the job should be routed from among the several that could perform the next operation required. Periodically solve an assignment model to obtain acceptable control decisions. q Suppose that the 8 fictitious jobs i of Table 10. 2 are either waiting for movement to their next workstation or will finish their current operation within the next 5 minutes. Processing times in the table short-term time implications of assigning jobs i to stations j. (transportation time to the station) + (weighting time until the station becomes free) + (operation processing time at the station) Opt Theory 2019 31

TABLE 10. 2 Transportation and Processing Times for CAM Assignment Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 33

q Opt Theory 2019 34

10. 8 Maximum Flows and Minimum Cuts q Opt Theory 2019 35

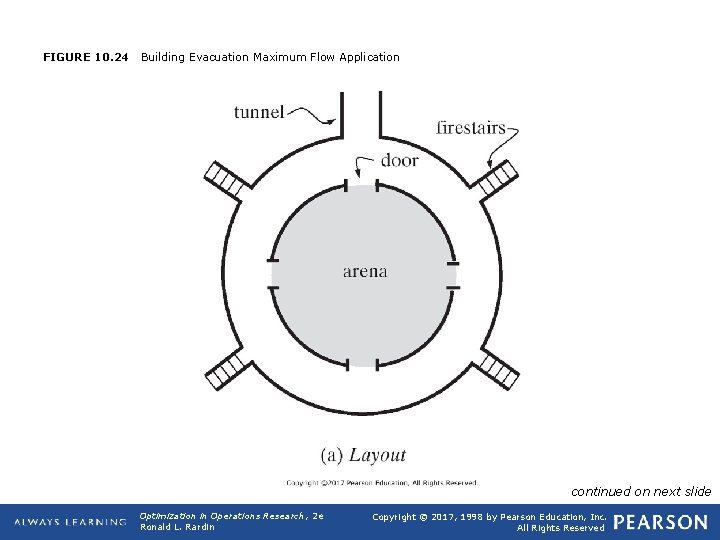
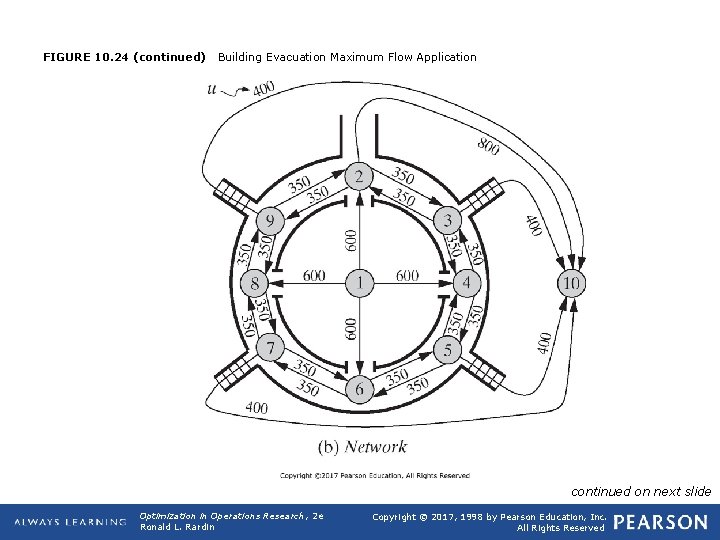
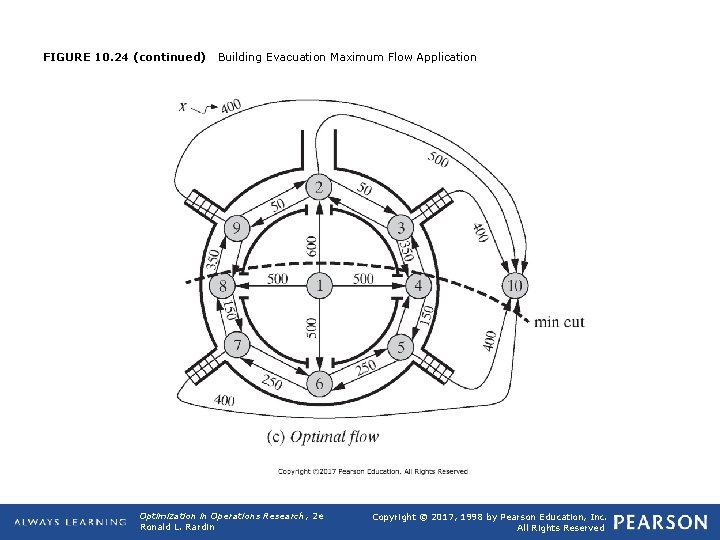
q Application 10. 5: Building Evacuation Maximum Flow Ø Based in part on L. G. Chalmet. R. L. Frances. and P. B. Saunders (1982). "Network Models for Building Evacuation, " Management Science, 28, 86 -105. All numerical data and diagrams were made up by the author of this book q Evaluate the capacity for building evacuation in the event of an emergency (Figure 10. 24, sports arena). Exit through doors on all four sides that can accommodate 600 persons per minute" Those doors lead into an outer hallway that can move 350 persons per minute in each direction. Egress from the hallway is through four firestairs with capacity 400 persons per minute and a tunnel to the parking lot accommodating 800 persons per minute. Our interest is in the maximum rate of evacuation possible with this design. Opt Theory 2019 36

FIGURE 10. 24 Building Evacuation Maximum Flow Application continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

FIGURE 10. 24 (continued) Building Evacuation Maximum Flow Application continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

FIGURE 10. 24 (continued) Building Evacuation Maximum Flow Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 40

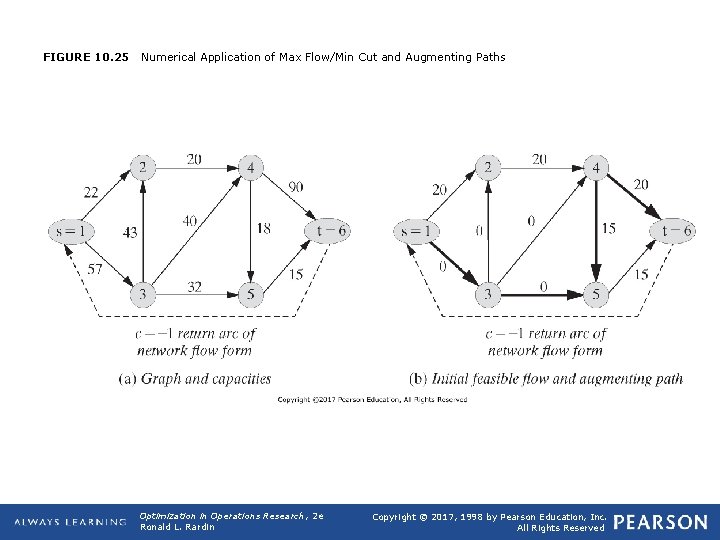
FIGURE 10. 25 Numerical Application of Max Flow/Min Cut and Augmenting Paths Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 42

q OR-Opt. 2019 43

q OR-Opt. 2019 44

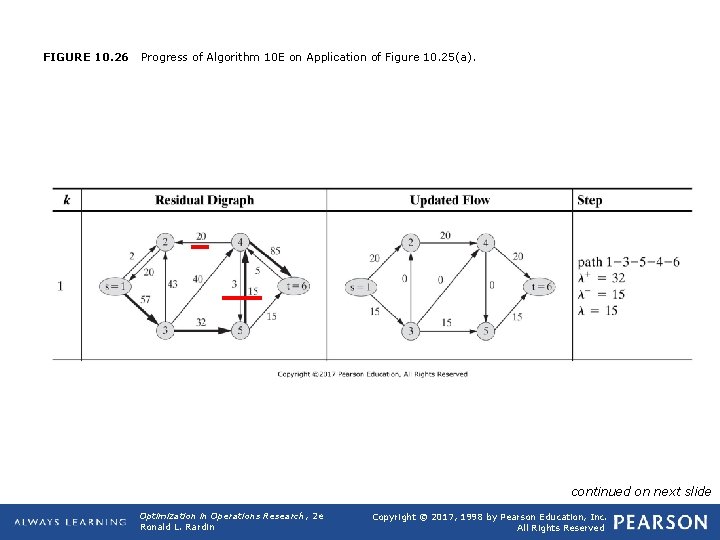
FIGURE 10. 26 Progress of Algorithm 10 E on Application of Figure 10. 25(a). continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

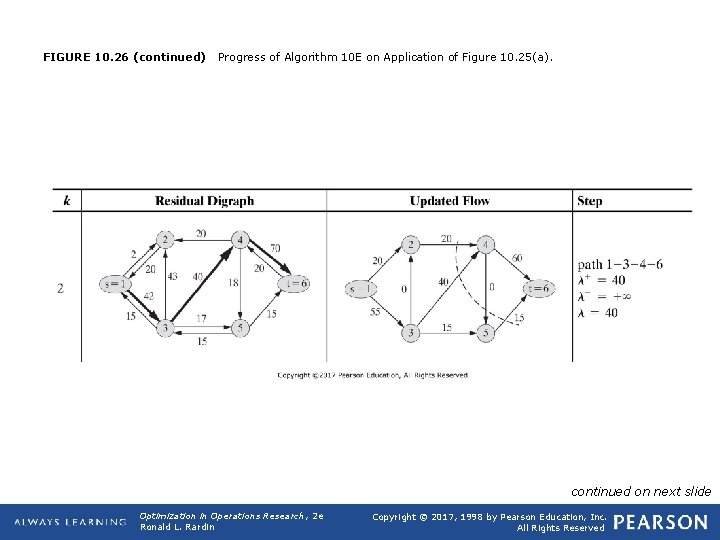
FIGURE 10. 26 (continued) Progress of Algorithm 10 E on Application of Figure 10. 25(a). continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

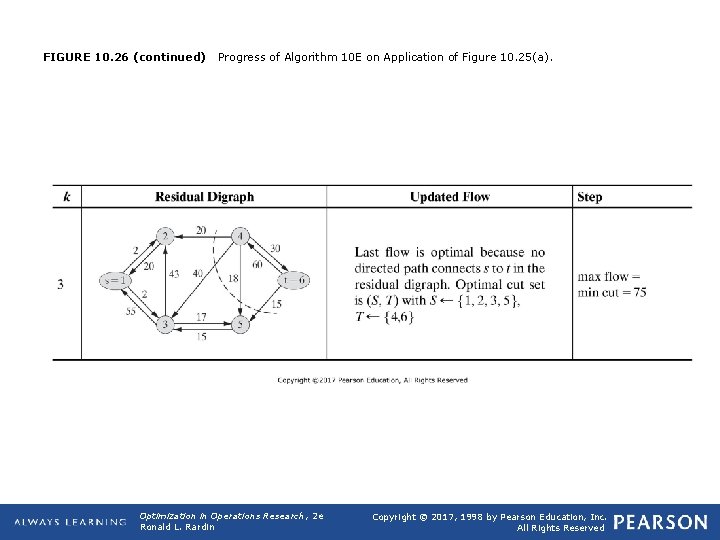
FIGURE 10. 26 (continued) Progress of Algorithm 10 E on Application of Figure 10. 25(a). Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 48

q Opt Theory 2019 49

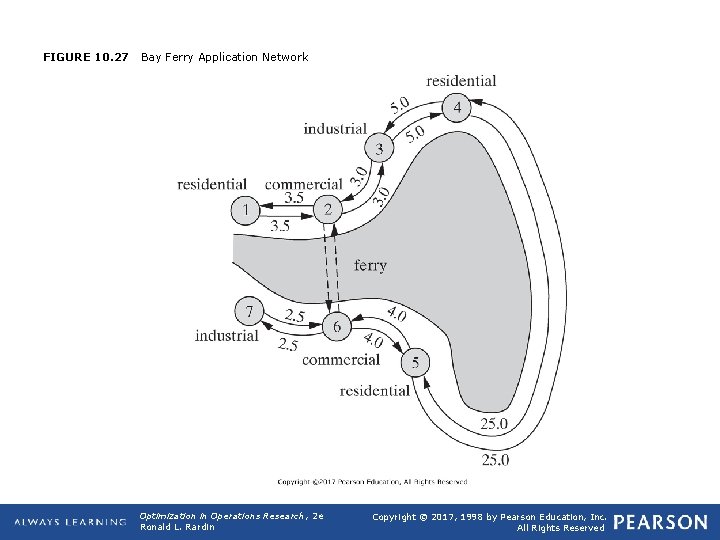
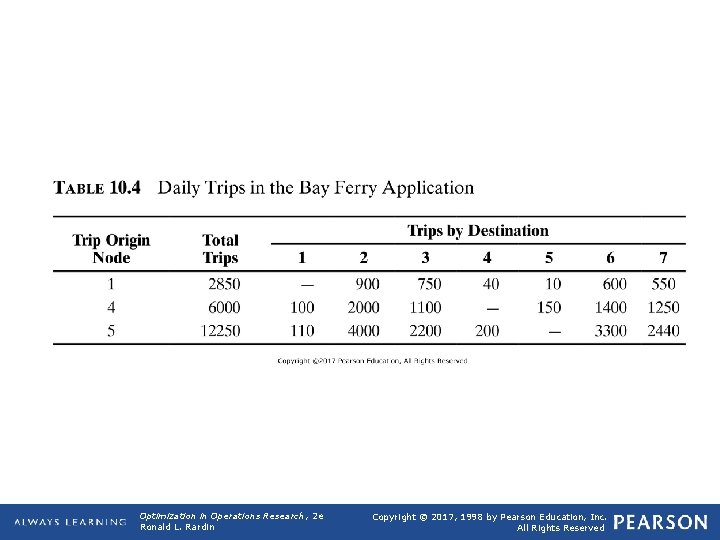
10. 9 Multicommodity and Gain/Loss Flows q Multicommodity Flows q Min cost netwok flow model assumes a single commodity. But multiple commodities may share a common network. q Def 10. 56: Multicommodity flow models seek a minimum cost flow where separate commodities are moving through a common network. q Application 10. 6: Bay Ferry Multicommodity Flow q Figure 10. 27 depicts traffic flows in communities around an ocean bay. Each morning, the population of the three residential communities travels to the two industrial and two commercial centers in the region. Table 10. 4 details flows by origin and destination. q The 21, 100 trips arising daily in the three residential communities produce a total of 399, 250 kilometers of driving. Consider operating a ferry connecting nodes 2 and 6 with capacity 2000 cars in each direction. Effect? Opt Theory 2019 50

FIGURE 10. 27 Bay Ferry Application Network Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

TABLE 10. 4 Daily Trips in the Bay Ferry Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 53

q Opt Theory 2019 54

TABLE 10. 5 Bay Ferry Application Model continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

TABLE 10. 5 (continued) Bay Ferry Application Model continued on next slide Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

TABLE 10. 5 (continued) Bay Ferry Application Model Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 58

q Opt Theory 2019 59

q Opt Theory 2019 60

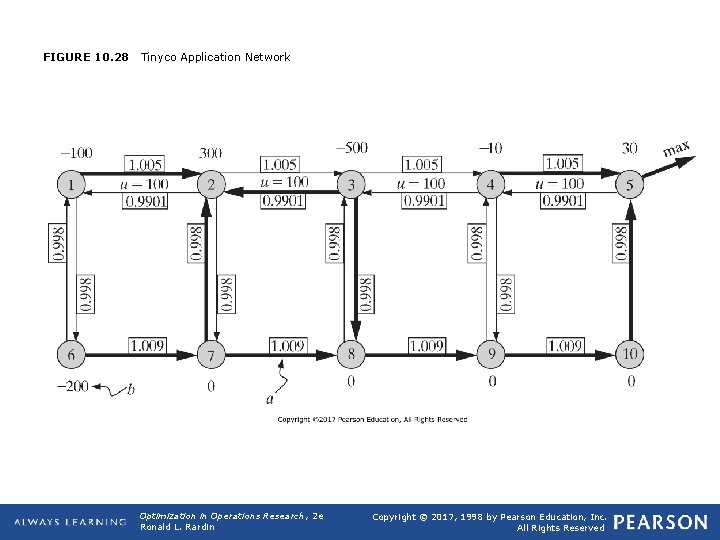
FIGURE 10. 28 Tinyco Application Network Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 62

TABLE 10. 6 Optimization in Operations Research, 2 e Ronald L. Rardin Tinyco Application Model Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

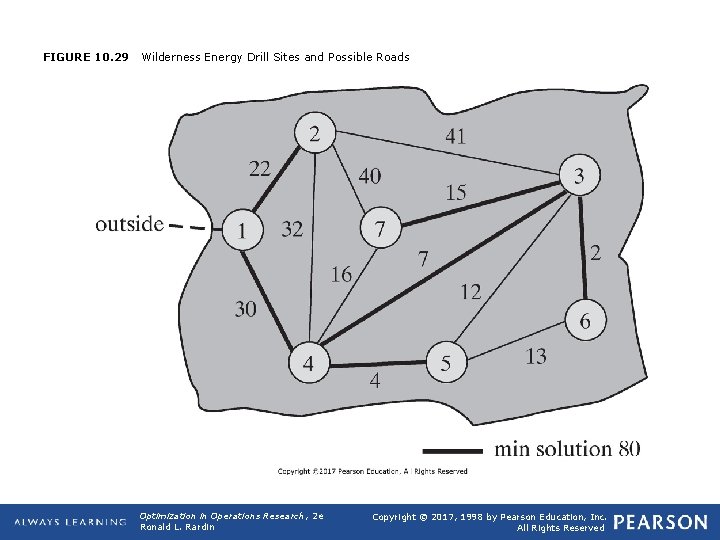
10. 10 Min/Max Spanning Trees q Application 10. 8: Wilderness Energy (WE) q Wilderness Energy (WE), a natural gas drilling company, wants to build roads to facilitate travel to/from and among drilling sites in a wilderness area it controls (Figure 10. 29). Have possible road alignments between pairs of sites that have been identified, including the estimated cost to construct each (in $ thousand). Want to connect every pair of sites with minimum total cost. q Minimum/Maximum Spanning Trees and the Greedy Algorithm q For WE problem, want a minimum spanning tree solution. Min/max spanning tree problem can be solved by a greedy algorithm (Kruskal’s algorithm, Prim’s algorithm). Opt Theory 2019 64

FIGURE 10. 29 Wilderness Energy Drill Sites and Possible Roads Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 66

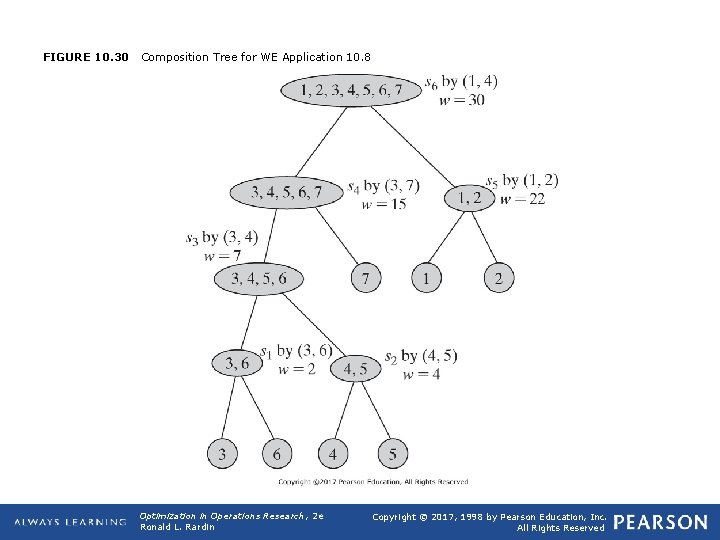
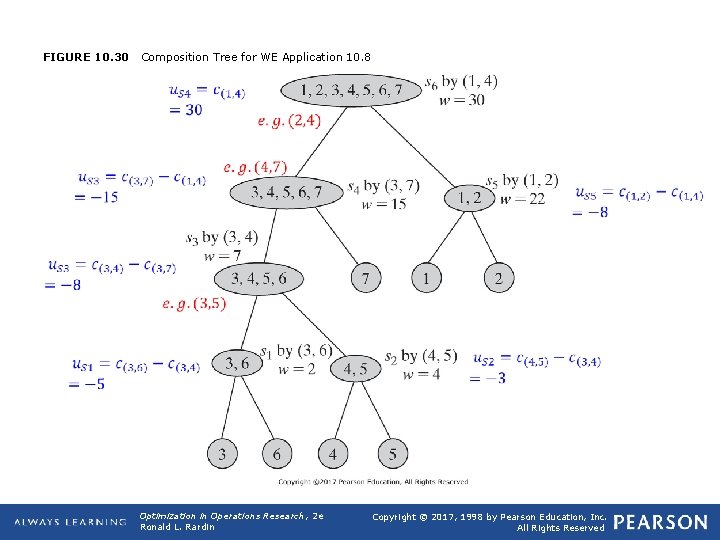
FIGURE 10. 30 Composition Tree for WE Application 10. 8 Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 68

q Opt Theory 2019 69

q Opt Theory 2019 70

FIGURE 10. 30 Composition Tree for WE Application 10. 8 Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 72

q Remarks: Proof show that for any objective function, the LP relaxation of formulation (10. 64) gives an integer optimal solution, which implies that the LP relaxation of (10. 64) has only integer extreme points. Hence the convex hull of the feasible integer solution of (10. 64) is same as the polyhedron defined by the LP relaxation of (10. 64) (details later in integer programming) q The LP relaxation of the cut-set formulation doesn’t have such property. It is a weaker formulation. q Spanning tree result is a special case of a mathematical object called matroid. The proof is also from the results of martoid (though dual variable values are different) q (10. 68) can be used for an algorithm (called 1 -tree relaxation based branch-andbound) to solve the traveling salesman problem. It can help us understand why the algorithm performs well. Details not here. Opt Theory 2019 73