Being Bayesian About Network Structure A Bayesian Approach

Being Bayesian About Network Structure A Bayesian Approach to Structure Discovery in Bayesian Networks Nir Friedman and Daphne Koller 04/21/2005 CS 673 1

Roadmap • Bayesian learning of Bayesian Networks – Exact vs Approximate Learning • Markov Chain Monte Carlo method – MCMC over structures – MCMC over orderings • Experimental Results • Conclusions 04/21/2005 CS 673 2
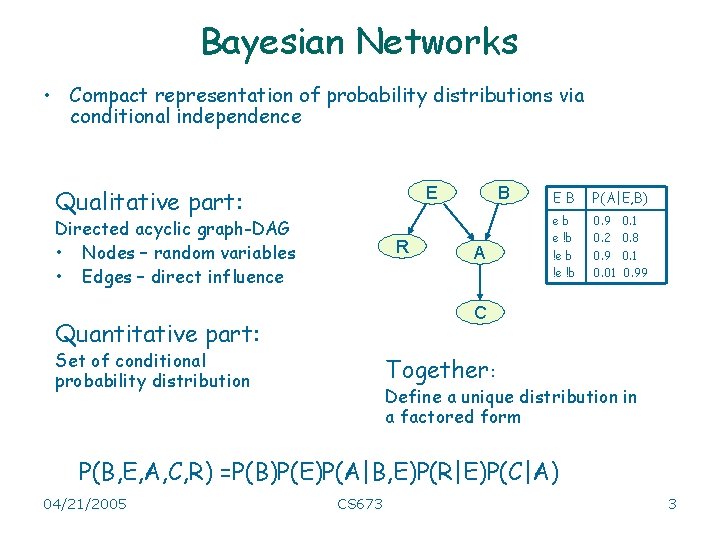
Bayesian Networks • Compact representation of probability distributions via conditional independence E Qualitative part: Directed acyclic graph-DAG • Nodes – random variables • Edges – direct influence R B A EB P(A|E, B) eb e !b !e !b 0. 9 0. 2 0. 9 0. 01 0. 8 0. 1 0. 99 C Quantitative part: Set of conditional probability distribution Together: Define a unique distribution in a factored form P(B, E, A, C, R) =P(B)P(E)P(A|B, E)P(R|E)P(C|A) 04/21/2005 CS 673 3

Why Learn Bayesian Networks? • Conditional independencies & graphical representation capture the structure of many real-world distributions - Provides insights into domain • Graph structure allows “knowledge discovery” • Is there a direct connection between X & Y • Does X separate between two “subsystems” • Does X causally affect Y • Bayesian Networks can be used for many tasks – Inference, causality, etc. • Examples: scientific data mining - Disease properties and symptoms - Interactions between the expression of genes 04/21/2005 CS 673 4
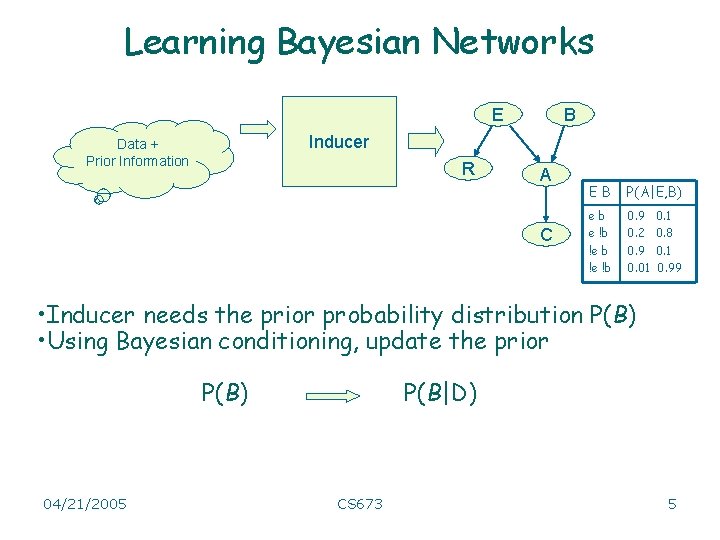
Learning Bayesian Networks E B Inducer Data + Prior Information R A C EB P(A|E, B) eb e !b !e !b 0. 9 0. 2 0. 9 0. 01 0. 8 0. 1 0. 99 • Inducer needs the prior probability distribution P(B) • Using Bayesian conditioning, update the prior P(B) 04/21/2005 P(B|D) CS 673 5
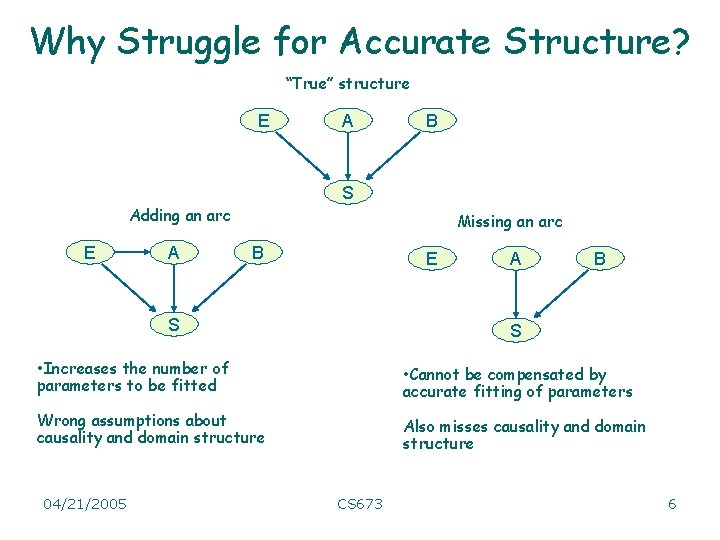
Why Struggle for Accurate Structure? “True” structure E A B S Adding an arc E A Missing an arc B E S A B S • Increases the number of parameters to be fitted • Cannot be compensated by accurate fitting of parameters Wrong assumptions about causality and domain structure Also misses causality and domain structure 04/21/2005 CS 673 6

Score-based learning • Define scoring function that evaluates how well a structure matches the data E, B, A <Y, N, N> <Y, Y, Y> <N, Y, Y>. . <N, N, N> E E B E A A B B A • Search for a structure that maximizes the score 04/21/2005 CS 673 7
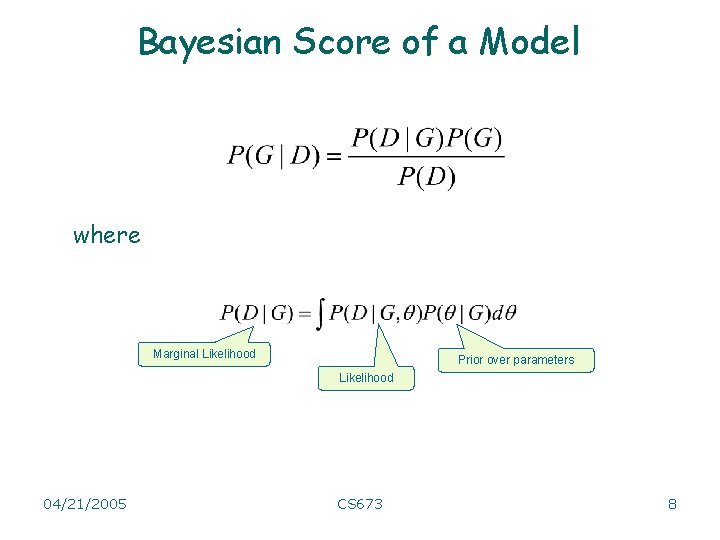
Bayesian Score of a Model where Marginal Likelihood Prior over parameters Likelihood 04/21/2005 CS 673 8
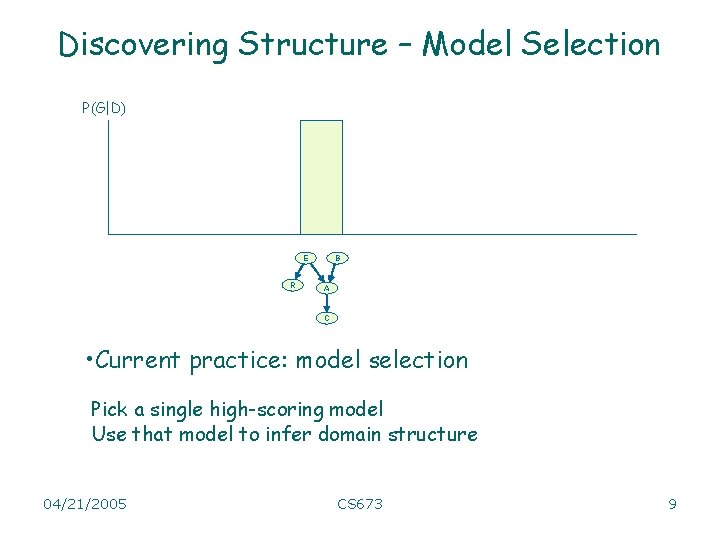
Discovering Structure – Model Selection P(G|D) E R B A C • Current practice: model selection Pick a single high-scoring model Use that model to infer domain structure 04/21/2005 CS 673 9
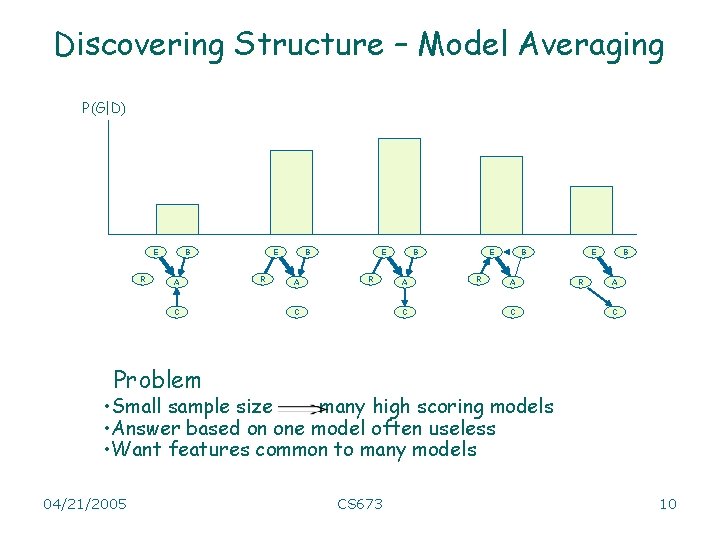
Discovering Structure – Model Averaging P(G|D) E R B A C E R B A E R C B A C E R B A C Problem • Small sample size many high scoring models • Answer based on one model often useless • Want features common to many models 04/21/2005 CS 673 10
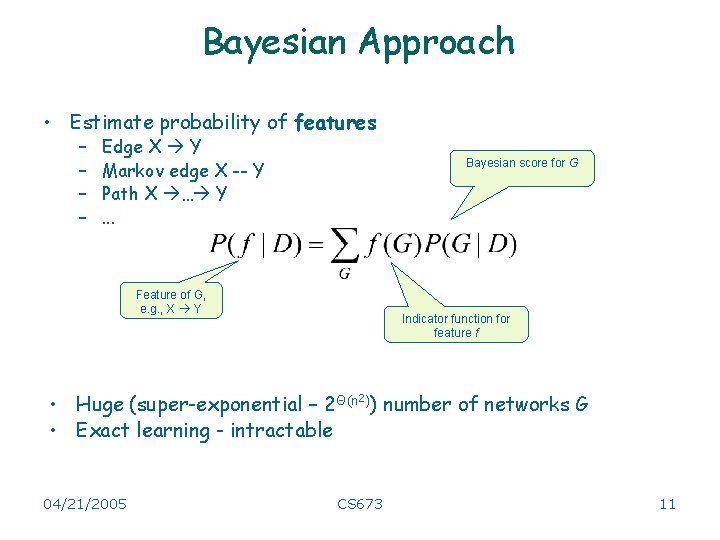
Bayesian Approach • Estimate probability of features – – Edge X Y Markov edge X -- Y Path X … Y. . . Bayesian score for G Feature of G, e. g. , X Y Indicator function for feature f • Huge (super-exponential – 2Θ(n 2)) number of networks G • Exact learning - intractable 04/21/2005 CS 673 11

Approximate Bayesian Learning • Restrict the search space to Gk, where Gk – set of graphs with indegree bounded by k -space still super-exponential • Find a set G of high scoring structures – Estimate - Hill-climbing – biased sample of structures 04/21/2005 CS 673 12

Markov Chain Monte Carlo over Networks MCMC Sampling – Define Markov Chain over BNs – Perform a walk through the chain to get samples G’s whose posteriors converge to the posterior P(G|D) of the true structure • Possible pitfalls: – Still super-exponential number of networks – Time for chain to converge to posterior is unknown – Islands of high posterior, connected by low bridges 04/21/2005 CS 673 13

Better Approach to Approximate Learning • Further constraints on the search space – Perform model averaging over the structures consistent with some know (fixed) total ordering ‹ • Ordering of variables: – X 1 ‹ X 2 ‹…‹ Xn parents for Xi must be in X 1, X 2, …, Xi-1 • Intuition: Order decouples choice of parents – Choice of Pa(X 7) does not restrict choice of Pa(X 12) Can compute efficiently in closed form • Likelihood P(D|‹) • Feature probability P(f|D, ‹) 04/21/2005 CS 673 14

Sample Orderings We can write Sample orderings and approximate MCMC Sampling • Define Markov Chain over orderings • Run chain to get samples from posterior P(<|D) 04/21/2005 CS 673 15
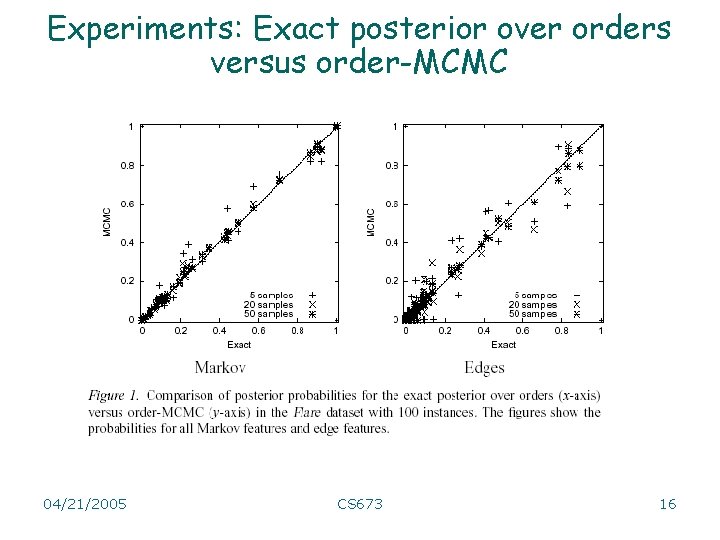
Experiments: Exact posterior over orders versus order-MCMC 04/21/2005 CS 673 16
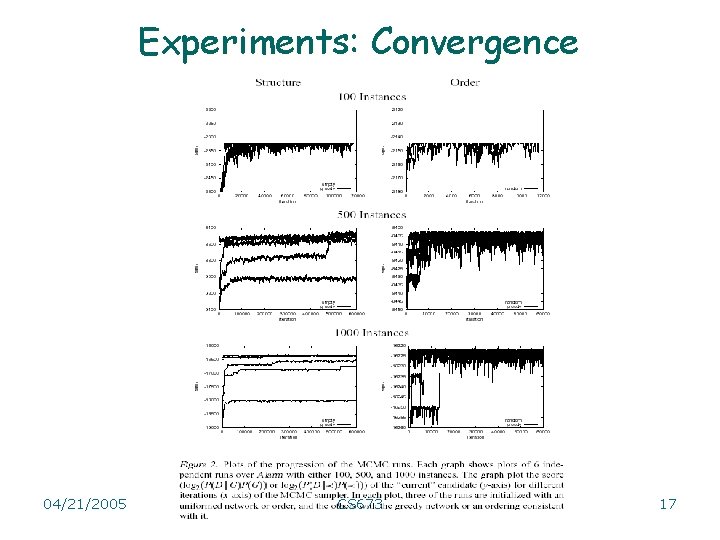
Experiments: Convergence 04/21/2005 CS 673 17
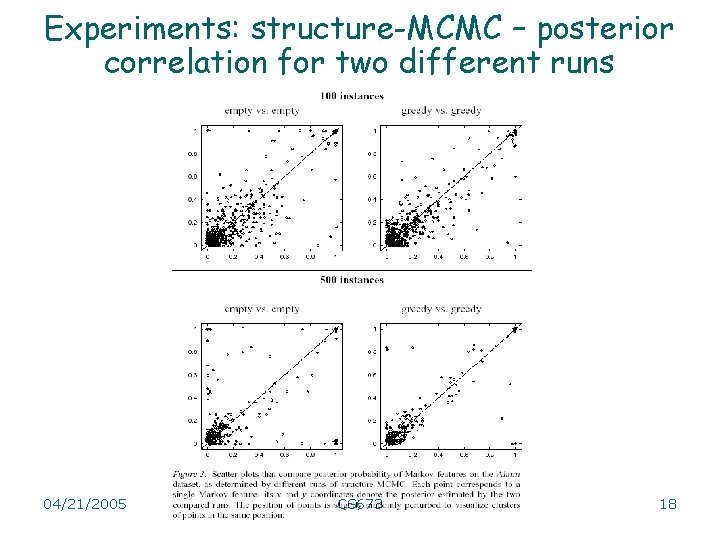
Experiments: structure-MCMC – posterior correlation for two different runs 04/21/2005 CS 673 18
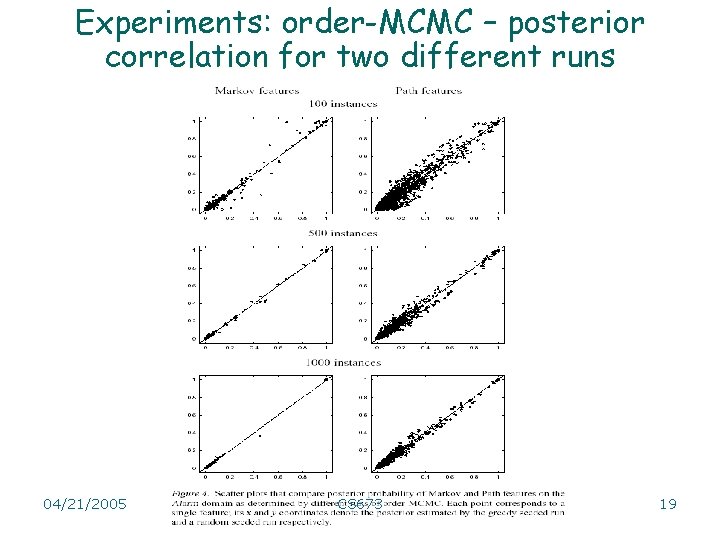
Experiments: order-MCMC – posterior correlation for two different runs 04/21/2005 CS 673 19

Conclusion • Order-MCMC better than structure-MCMC 04/21/2005 CS 673 20

References Being Bayesian about Network Structure: A Bayesian Approach to Structure Discovery in Bayesian Networks, N. Friedman and D. Koller. Machine Learning Journal, 2002 NIPS 2001 Tutorial on learning Bayesian networks from Data. Nir Friedman and Daphne Koller Nir Friedman and Moises Goldzsmidt, AAAI-98 Tutorial on learning Bayesian networks from Data. D. Heckerman. A Tutorial on Learning with Bayesian Networks. In Learning in Graphical Models, M. Jordan, ed. . MIT Press, Cambridge, MA, 1999. Also appears as Technical Report MSR-TR-95 -06, Microsoft Research, March, 1995. An earlier version appears as Bayesian Networks for Data Mining, Data Mining and Knowledge Discovery, 1: 79 -119, 1997. Christophe Andrieu, Nando de Freitas, Arnaud Doucet and Michael I. Jordan. An Introduction to MCMC for Machine Learning, 2002. Artificial Intelligence: A Modern Approach. Stuart Russell and Peter Norvig 04/21/2005 CS 673 21
- Slides: 21









































