Answer True or False and justify your answer

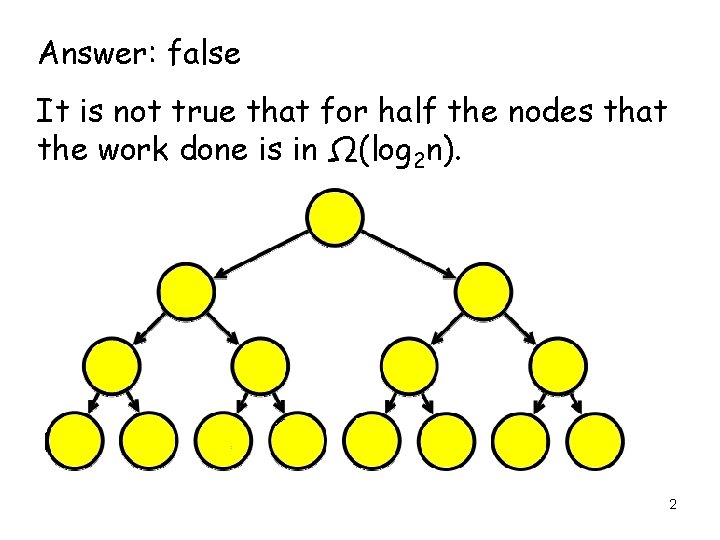
Answer True or False and justify your answer: The following Heapify routine takes time Ω(n log 2 n) because for at least half of the bubble. Down operations, the time it takes is in Ω(log 2 n) and therefore the time is in Ω(n/2 log 2 n) Ω(nlog 2 n). for (i= (n-2)/2; i ≥ 0; i--) bubble. Down the node in A[i]; 1

Answer: false It is not true that for half the nodes that the work done is in Ω(log 2 n). 2

Question #2 on Assignment #3: 2. The aim of this question is to analyze the time complexity of the following build heap routine: heapify(r) If r is not null 1. Heapify the left subtree. 2. Heapify the right subtree. 3. Bubble down the key at node r. T(n) = log 2(n +1) + 2 T((n -1)/2), T(1) = 1. Solution: T(2 k- 1)= 2 k+1 – k – 2 ≤ 2 * n So T(n) is in O(n) which is not in Ω(n log 2 n). 3

The possibilities for a final exam tutorial: Tues. Dec. 15: 12: 30 Wed. Dec. 16: 12: 30 Thurs. Dec. 17: 12: 30 We’ll vote on one today and then I will book a classroom for the tutorial. Final: Friday Dec. 18 at 9 am. 4

Proving that Programs Work Correctly A loop invariant is a statement S which is true each time we enter a particular point of a loop. Induction is generally used to prove that a loop invariant is true. 5

Loop from our Max. Sort algorithm: max. Pos=0; for (i= 1; i <= end; i++) { if (A[i] > A[max. Pos]) max. Pos= i; } Loop invariant: At the end of the kth iteration of the loop, max. Pos is the position of the first occurrence of a maximum element in A[0. . k]. 6

Loop invariant: At the end of the kth iteration of the loop, max. Pos is the position of the first occurrence of a maximum element in A[0. . k]. Proof (by induction). [Basis] If k=0, max. Pos=0 which is the position of the maximum element of A[0… 0]. [Inductive step] We assume the loop invariant holds for k. We prove it holds at the end of iteration k+1. Note i=k+1 during iteration k+1. 7

At iteration k+1 (i=k+1): A[k+1]=A[i] is the first occurrence of a maximum value in A[0…(k+1)] if and only if it is greater the maximum of A[0…k] which by induction is A[max. Pos]. If it is larger, max. Pos is set to k+1, and otherwise, the value of max. Pos is unchanged. In either case it equals the position of the first occurrence of a maximum element of A[0…(k+1)] as required. 8

Theorem: The final list at the end of the radix sort algorithm contains the data values in sorted order. Proof: Uses a loop invariant. 9

for (i=0; i < k; i++) x= dk-1, dk-2, . . . , d 2, d 1, d 0. for (j=0; j < r; j++) Pseudo code Set Lj to be an empty list. while (L is not empty) do Take the first cell off the front of L. Let d be digit i of the key value x stored in this cell. Add this cell to the end of the list Ld. endwhile Set L to be an empty list. for (j=0; j < r; j++) Append Lj to the end of L. 10

This algorithm works because it is stable: amongst keys with equal value, their relative orders are preserved. The formal proof of correctness applies the following loop invariant. Loop invariant: In the outer for loop, just before the iteration with a particular value of i, the integers in L are sorted according to the values induced by their last i digits, di-1, . . . , d 2, d 1, d 0. Proof (by induction). [Basis] This statement implies that before the iteration with i=0, they are not sorted at all. This is trivially true. 11

[Induction step] Assume that just before the iteration with a particular value of i, the integers in L are sorted according to the integers induced by their last i digits. We want to prove that after the iteration with i, the values in L are sorted according to the integers induced by their last i+1 digits, di-1, . . . , d 2, d 1, d 0. 12

They are placed into the linked lists (Ld's) so that things that are last in the array end up at the end of the lists. Now when you append things together, the integers are ordered according to their ith digit di. Amongst those with the same ith digit, they fall into the same order as they were in L and hence by induction, these are sorted by di-1, di-2, . . . , d 2, d 1, d 0. So at the end of this iteration, the values are sorted according to di, di-1, . . . , d 2, d 1, d 0. 13

Note that this same technique could also be used to sort for other data types such as strings. Suppose for example you wanted to sort strings of length k over the 26 character alphabet {a-z}. You could then use 26 lists, one for each character. 14

What is the time for radix sort? If the integers have k digits then it takes time θ(k n + r) which is in θ(n) if k and r are constants. This is not a contradiction to the assertion that any comparison model sorting algorithm takes Ω(n log n) time: radix sort examines individual digits of the data items which is not allowed in the comparison model. 15