An Introduction to Classification Classification vs Prediction Classification

An Introduction to Classification • Classification vs. Prediction • Classification & ANOVA • Classification Cutoffs, Errors, etc. • Multivariate Classification & Linear Discriminant Function

An Introduction to Classification Let’s start by reviewing what “prediction” is… Using a person’s scores on one or more variables to make a “best guess” of the that person’s score on another variable (the value of which isn’t known) Classification is very similar … Using a person’s scores on one or more variables to make a “best guess” of the category to which that person belongs (when the category type isn’t known). The difference -- a language “convention” • if the “unknown variable” is quantitative -- its called prediction • if the “unknown variable” is qualitative -- its called classification

How does classification work? ? ? Let’s start with an “old friend” -- ANOVA In its usual form… • There are two qualitatively different IV groups • naturally occurring or “created” by manipulation • A quantitative DV • H 0: Mean. G 1 = Mean G 2 • Rejecting H 0: tells us • There is a relationship between the grouping and DV • Groups represent populations with different means on the DV • Knowing what group a person in allows us to guess their DV score -- mean of that group

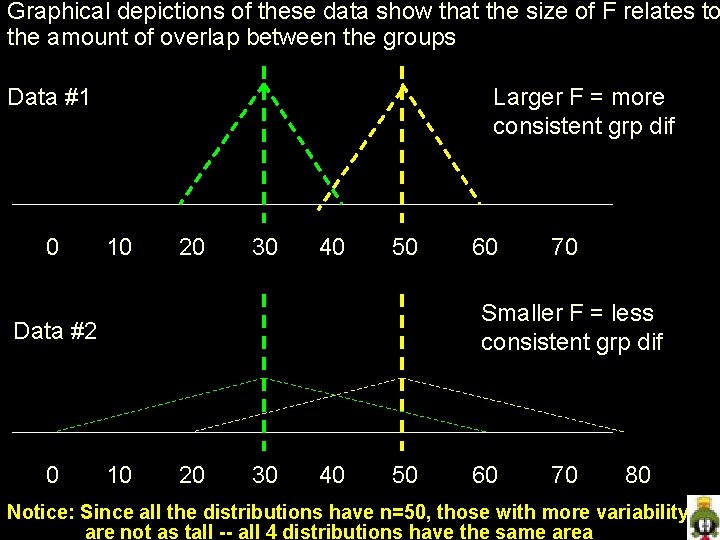
Let’s review in a little more detail… Remember the formula for the ANOVA F-test variation between groups size of the mean difference F = --------------------------------------variation within groups In words -- F compares the mean difference to the variability around each of those means Which of the following will produce the larger F-test ? The two data sets have the same means, mean difference & N but the difference is…. Data #2 (@ n = 50) Data #1 (@ n = 50) group 1 mean = 30 std dev = 5 group 1 mean = 30 std dev = 15 group 2 mean = 50 std dev = 15

Graphical depictions of these data show that the size of F relates to the amount of overlap between the groups Data #1 0 Larger F = more consistent grp dif 10 20 30 40 50 70 Smaller F = less consistent grp dif Data #2 0 60 10 20 30 40 50 60 70 80 Notice: Since all the distributions have n=50, those with more variability are not as tall -- all 4 distributions have the same area

Let’s consider that last one “in reverse”… Could knowing the person’s score help tell us what qualitative group they are in? …to “classify” them to the proper group? an Example… Research has revealed a statistical relationship between the number of times a person laughs out loud each day (quant variable) and whether they are depressed or schizophrenic (qual grouping variable). Mean laughs. Depressed = 4. 0 Mean laughs. Schizophrenic = 7. 0 F(1, 34) = 7. 00, p <. 05 A new (as yet undiagnosed) patient laughs 11 times the first day what’s your “classification” depressed or schizophrenic? Another patient laughs 1 time -- your “classification”? A third new patient laughs 5 times -- your “classification”?

Why were the first two “gimmies” and the last one not? • When the groups have a mean difference, a score beyond one of the group means is more likely to belong to that group than to belong to the other group (unless stds are huge) • someone who laughs more than the mean for the schizophrenic group is more likely to be schizohrenic than to be depressed • someone who laughs less than the mean of the depressive group is more likely to be depressed than to be schizophrenic • Even when the groups have a mean difference, a score between the group means is harder to correctly classify (unless stds are miniscule) • someone with 5 -6 laughs are hardest to classify, because several depressed and schizophrenic folks have this score

Here’s a graphical depiction of the clinical data. . . o X 18 schiz. patients x x xo o o mean laughs = 4. 0 x x x ox ox o o o mean laughs = 7. 0 x x x ox ox o o o 18 dep. patients laughs --> 0 1 2 3 4 5 6 7 8 9 0 1 2 Looking at this, its easy to see why we would be. . . • confidant in an assignment based on 11 laughs • no depressed patients had a score that high • confident in an assignment based on 1 laugh • no schizophrenic patients had a score that low • lacking confidence in an assignment based on 5 or 6 laughs • several depressed & schizophrenic patients had 5 or 6

The process of prediction required two things… • that there be a linear relationship between the predictor and the criterion (reject H 0: r = 0) • a formula (y’ = bx + a) to “translate” a predictor score into an estimate of a criterion variable score Similarly, the process of classification requires two things … • a statistical relationship between the predictor (DV) & criterion (reject H 0: M 1 = M 2) • a cutoff to “translate” a person’s score on the predictor (DV) into an assignment to one group or the other • where should be place the cutoff? ? ? • Wherever gives us the most accurate classification !!

X 18 dep. patients mean laughs = 4. 0 o x x xo o o 18 schiz. patients x x x ox ox o o o mean laughs = 7. 0 x x x ox ox o o o laughs --> 0 1 2 3 4 5 6 7 8 9 0 1 2 1 1 1 When your groups are the same size and your group score distributions are symmetrical, things are pretty easy… • place the cutoff at a position equidistant from the group means • here, the cutoff would be 5. 5 -- equidistant between 4. 0 and 7. 0 • anyone who laughs more than 5. 5 times would be “assigned” as schizophrenic • anyone who laughs fewer than 5. 5 times would be “assigned” as depressed

o x xo o o 18 schiz. patients x x x ox ox o o o mean laughs = 7. 0 18 dep. patients mean laughs = 4. 0 x x x ox ox o o o laughs --> 0 1 2 3 4 5 6 7 8 9 0 1 2 1 1 1 We can assess the accuracy of the assignments by building a “reclassification table” Actual Diagnosis Assignment Depressed Schizophrenic 14 4 4 14 reclassification accuracy would be 28/36 = 77. 78%

When considering simple regression/prediction, we wanted to be able to compare two potential predictors to determine if one would be better -- we used Steiger’s Z-test of H 0: ry, x 1= ry, x 2 How do we compare two potential classification variables to determine if one is a better basis for accurate classification ? • We do it the same way (with one intermediate step) • As you might remember from ANOVA, we can express the “effect size” associated with any F as r (or - same thing) • r = [ F / (F + dferror)] • So, to compare two potential classification variables • compute the ANOVA for each variable (on same sample) • convert each F to r • compare the r values using Steiger’s Z-test • remember that you’ll need the correlation between the two classification variables (rx 1, x 2)

An example, Which provides better classification between schiz vs. depression, # times laughing out loud, or score on a “depression scale”? • For laughing out loud F(1, 34) = 7. 00 -- translates to r = [ F / (F + dferror)] = [ 7. 0 / (7. 0 + 34)] =. 413 • For the depression scale F(1, 34) = 4. 0 -- translates to r = [ F / (F + dferror)] = [ 4. 0 / (4. 0 + 34)] =. 324 • # laughs and depression scale scores are correlated r =. 35 • So using Steiger’s Z-test Z =. 495, p >. 05 • so there is no advantage of using one of these predictors over the other • the apparent difference in r is not greater than chance

When considering simple regression/prediction, we wanted to be able to compare the same correlation in two different populations - we used Fisher’s Z-test of H 0: ry, x 1(pop 1) = ry, x 1(pop 2) How compare the same correlations in two populations to determine if one population would have more accurate assignments ? As you might remember from ANOVA, we can express the “effect size” associated with any F as r (or - same thing) • r = [ F / (F + dferror)] for each population So, to compare two potential classification variables • compute the ANOVA for each sample • convert each F to r • compare the r values using Fisher’s Z-test

An example, Does # times laughing out loud discriminate between schiz vs. depression better for in-patients or for out-patients. • For in-patients F(1, 48) = 12. 00 -- translates to r = [ F / (F + dferror)] = [ 12. 0 / (12. 0 + 48)] =. 447 Fisher’s Z transformation of =. 45 is. 485 • For the out-patients F(1, 88) = 2. 0 -- translates to r = [ F / (F + dferror)] = [ 2. 0 / (2. 0 + 88)] =. 149 • Fisher’s Z = 1. 86 • Z(p=. 05) = 1. 96, so retain H 0: -- same discriminability in both pops

Getting ready for ldf… • multiple regression works better than simple regression because a y’ based on multiple predictors is a better estimate of y than a y’ based on a single predictor • similarly, classification based on multiple predictors will do better than classification based on a single predictor • but, how to incorporate multiple predictors into a classification ? ? • Like with multiple regression, multiple variables (Xs) are each given a weighting and a constant is added • ldf = b 1* X 1 + b 2* X 2 + b 3* X 3 + a • the composite variable is called a linear discriminant function • function -- constructed from another variables • linear -- linear combination of linearly weighted vars • discriminant -- weights are chosen so that the resulting has the maximum possible F-test between the groups

So, how does this all work ? ? ? • We start with a grouping variable and a set of quantitative (or binary) predictors (what would be DVs if doing ANOVAs) • using an algorithm much like multiple regression, the bivariate relationship of predictor to the grouping variable & the collinearities among the predictors are all taken into account and the weights for the ldf formula are derived • remember this ldf will have the largest possible F value between the groups • a cutoff value for the ldf is chosen the cutoff is chosen (more fancy computation) to maximize % correct reclassification • to “use” the formula • a person’s values on the variables are put into the formula & their ldf score is computed • their score is compared to the cutoff, and they are assigned to one group or the other

“ldf Questions” (very parallel to “regression questions”) • ANOVA -- can groups be discriminated using the quant var? • Does one quant variable work better than another to discriminate the groups? (Steiger’s Z-test to compare the r for the two quant variables • Does a quant variable better discriminate between groups for one population than another? (Fisher’s Z-test to compare the r from the two populations) • ldf - can groups be discriminated using a combination of vars? • Comparison of nested ldf models (X 2 -change test & Mc. Nemar’s X 2) • Comparison of non-nested ldf models (Mc. Nemar’s X 2) • Comparison of models across populations (R 2 & Mc. Nemar’s X 2) • Comparison of models across classification rules (Mc. Nemar’s X 2)