A differencilszmts alkalmazsai A diasorozat az Analzis 2

A differenciálszámítás alkalmazásai A diasorozat az Analízis 2. (Mozaik Kiadó 2005. ) c. könyvhöz készült. Készítette: Dr. Ábrahám István 1

A differenciálszámítás segítségével egzakt módon leírhatunk minden mozgást. Így széleskörű a deriválás felhasználása különböző tudományágakban. Leggyakrabban a függvények (azaz a társadalmi és természeti törvények) különböző jellemzőit határozzák meg a differenciálszámítással. A differenciálható függvények vizsgálata A függvények optimális értékeit számolhatjuk ki, a növekedés és csökkenés szakaszait adhatjuk meg és még sok más információt nyerhetünk a függvényekről a deriválással. A függvény növekedése, fogyása Vizsgáljuk az x 0 -ban és környezetében folytonos f(x) függvényt. Ha f’(x 0)>0, akkor f(x) növekedően halad át az x 0 ponton. Az indoklás: felvesszük a pontbeli deriváltat, a differenciálhányadost: Ha egy szám (f’(x 0)) pozitív, akkor a vele egyenlő tört számlálója és nevezője azonos előjelű. Ha x pozitív, akkor a y is az, a függvény növekvő: Ha viszont a x negatív (az x 0 -tól balra vettük fel), akkor a y is, ami szintén növekedést jelent: 2

Példa: az f(x)=x 2– 2 x+3 függvénynél vizsgáljuk meg a derivált előjelét az x 0=2 pontban. Deriválás: f’(x)=2 x– 2, így tehát: f(2)=4– 2=2>0. Ez azt jelenti, hogy a függvény növekvően halad át az x 0=2 abszcisszájú ponton. Tudjuk: x 2– 2 x+3=(x– 1)2+2 és „elhittük”: a függvényünk (1; 2) csúcspontú egyenes állású parabola, amely a P 0(2; 3) ponton növekvően halad át. A differenciálhányados előjele viszont bizonyítja ezt! A differenciálhányados értéke azt is jelenti, hogy a ponthoz tartozó érintő iránytangense 2 (pozitív, tehát az érintő „emelkedő” egyenes). Megjegyzés: a differenciálhányados képzésnél x 0. Ha a függvény folytonos az x 0 környezetében, akkor a y előjele a határérték képzésnél változatlan marad. Ha f’(x 0)< 0, akkor f(x) csökkenően halad át az x 0 ponton. Az állítás indoklása teljesen analóg a növekvő függvénynél látottal. Példa: legyen ismét f(x)=x 2– 2 x+3, és most az x 0=0, 5. Az f’(x)=2 x– 2, tehát: f(0, 5)=– 1<0, ami csökkenést jelent. A függvény adott pontjához húzott érintő iránytangense negatív, az érintő „lejtős” egyenes. 3

Tétel: az [a; b]-on a (deriválható) f(x) függvény akkor és csak akkor monoton növekvő, ha a szakasz minden pontjában az első derivált nem negatív: f’(x) 0. Csökkenő a függvény, ha minden pontban f’(x) 0. Példa: adjuk meg az f(x)=x 2– 2 x+3 függvény monotonitási szakaszait! A derivált: f’(x)=2 x– 2, ahol f’(x)>0, ott növekvő a függvény: 2 x– 2>0, azaz x>1. Tehát az x>1 intervallumon a függvény végig (szigorúan monoton) növekvő. Ahol f’(x)<0, ott csökkenő a függvény, azaz az x<1 intervallumon. o o Definíció: az x 0 pontot a függvény stacionárius pontjának nevezzük, ha f’(x 0)=0. A stacionárius pontban az érintő iránytangense 0, azaz az érintő párhuzamos az x tengellyel. Példa: az f(x)=x 2– 2 x+3 deriváltja: f’(x)=2 x– 2, ott van stacionárius pont, ahol 2 x– 2=0. Tehát az x 0=1 helyen a függvénynek stacionárius pontja van. A Ps stacionárius pont y=2 „magasságban” van: Ps(1; 2), az érintő iránytangense 0. Tétel: ha az f(x) függvény az x 0 környezetében deriválható és az x 0 stacionárius pont, akkor: ha a derivált függvény az x 0 -ban előjelet vált, az f(x) függvénynek ebben a pontban helyi szélsőértéke van. A helyi szélsőértéket általában lehet „fordulópont értelemben vett” szélsőértéknek is nevezni. Ugyanis ebben a pontban „fordul át” a függvény csökkenőből növekvőbe, vagy növekvőből 4 csökkenőbe.

Belátni a tétel igazát egyszerű: Ha az x 0 „előtt”, azaz az x 0 -nál kisebb számok esetén a derivált negatív, az x 0 után pozitív, akkor a függvény az x 0 -ba csökkenően érkezik és növekvően megy tovább, tehát minimuma van. x 0 Ha viszont az x 0 „előtt” a derivált pozitív, az x 0 után negatív, akkor az f(x)-nek az x 0 -ban helyi maximuma van. Példa: az f(x)=x 2– 2 x+3 függvénynek az x 0 =1 helyen stacionárius pontja van. Az x 0 „előtt” (tőle balra) az f’(x) negatív, így az eredeti f(x) csökkenően érkezik ide. Az x 0 után (tőle jobbra) az f’(x) pozitív, tehát az eredeti f(x) növekvően halad tovább, így az x 0 -ban helyi minimum van. A minimum értéke, azaz az x 0 pontban felvett függvényérték 2. Írhatjuk így is: a helyi szélsőérték a függvényünknél: Pmin(1; 2). Megjegyzések 1. A stacionárius pontban nincs mindig szélsőérték! Szükséges a szélsőértékhez a derivált előjelváltása az x 0 -ban. Például az f(x)=x 3 esetén f’(x)=3 x 2, így az x 0=0 stacionárius pont. A derivált előjele az x 0=0 előtt is és után is pozitív, tehát a 0 helyen nincs szélsőérték! Érdekesség: az érintő iránytangense a 0 helyen 0, az érintő maga az x tengely. 5

2. Lehet helyi szélsőérték olyan pontban is, ahol a függvény nem differenciálható. Például az f(x)=lxl-nek az x 0=0 pontban lokális szélsőértéke van. Az lxl függvény – mint tudjuk – az x 0=0 helyen nem differenciálható. Példa: adott az függvény. Határozzuk meg az f(x) helyi szélsőértékéit és monotonitási szakaszait! Szélsőértéke egy mindenütt deriválható függvénynek ott lehet, ahol f’(x)=0. Megkeressük a stacionárius pontokat: f’(x)=x 2+2 x– 3=0, ebből: x 1=– 3 és x 2=1. Helyi szélsőérték lehet az x 1=– 3 és x 2=1 pontokban. A derivált előjele – 3 -tól balra, például – 4 helyen: f’(– 4)>0, tehát az f(x) a – 3 -hoz növekvően érkezik, – 3 után, például a – 2 helyen: f’(– 2)<0, azaz f(x) – 3 után csökkenően halad tovább. Így az x 1=– 3 helyen lokális maximum van, értéke=4. Írható így is: Pmax(– 3; 4). Az x 2=1 előtt f’(x)<0 (láttuk: f’(– 2)<0 ), az x 2 -től jobbra, például a 2 helyen: f’(2)>0. Így x 2 -ben a függvénynek helyi minimuma van. A minimum értéke: A függvény képe: A függvény folytonos (hatványfüggvény), így a „fordulópontjai”, a helyi szélsőértékek határozzák meg a monotonitási szakaszokat: ] – ; – 3]: az f(x) növekvő, [– 3; 1]: az f(x) csökkenő, [1; [: az f(x) növekvő. 6

Szélsőérték keresés a második deriválttal Tétel: ha az f(x) az x 0 pontban kétszer deriválható, szélsőértéke x 0 -ban akkor lehet, ha az első derivált értéke itt 0, azaz: f’(x 0)=0, és ha ebben a pontban a második derivált nem nulla, azaz: f’’(x 0) 0, akkor van szélsőérték. A szélsőérték minősége: ha f’’(x 0)>0, akkor x 0–ban helyi minimum van; ha f’’(x 0)<0, akkor x 0–ban helyi maximum van. Bizonyítás: ha f ’’(x 0)>0, akkor f ’(x) az x 0 -ban növekvő. Mivel f ’(x 0)=0, ezért az f ’(x) az x 0 előtt negatív, az x 0 után pozitív (az f ’(x) az x 0–ban „megy át” az x tengelyen, azaz vált előjelet). Tehát itt az f(x)-nek helyi minimuma van. A helyi maximumra teljesen analóg a bizonyítás Példa: az függvénynél az első derivált: f ’(x)=x 2+2 x– 3. Ennek zérushelyei: – 3 és 1. A második derivált függvény: f ”(x)=2 x+2. A második derivált értéke a – 3 hey’ lyen negatív, így az első derivált a – 3 -ban csökkenő. Az első derivált a – 3 -nál megy át az x tengelyen (azaz f ’(– 3)=0), így – 3 előtt pozitívak az első derivált függvényértékei, utána negatívak. Tehát a stacionárius pontban az első derivált előjelet vált. Így az eredeti f(x) függvénynek a – 3 helyen szélsőértéke van, ami helyi maximum. 7

A második deriváltakat felhasználó szélsőérték keresés nem túl egyszerű. Megfigyelhetjük, hogy tulajdonképpen „visszafelé” haladunk, a második derivált előjeléből az első derivált függvény menetére következtetünk először. Példa: adjuk meg az függvény szélsőértékeit és monotonitási szakaszait! Felhasználjuk az első és a második deriváltakat: Ott lehet szélsőérték, ahol f ’(x)=0, azaz: Ebből: x 1=– 1, x 2=0 és x 3=1. Akkor van szélsőérték ezeken a helyeken, ha a második derivált értéke nem nulla. A második derivált pontbeli előjeléből a szélsőérték minőségét is meg tudjuk adni. f”(– 1)<0, tehát az x 1=– 1 helyen van szélsőérték és ez maximum, értéke: f(– 1) 0, 3679. f”(0)>0, azaz az x 2=0 -nál minimum van, értéke 0. Összefoglalva : f”(1)<0, így az x 3=1 -nél is maximum van értéke e-1. Pmax(– 1; e-1), Pmin (0; 0), Pmax(1; e-1). A monotonitási szakaszok: ]– ; – 1] szakaszon f(x) növekvő, [– 1; 0]: csökkenő, [0; 1] : szintén növekvő, [1; [ : csökkenő. A függvény képe: A függvényünk folytonos, így a helyi szélsőértékek határozzák meg a monotonitási szakaszokat. 8

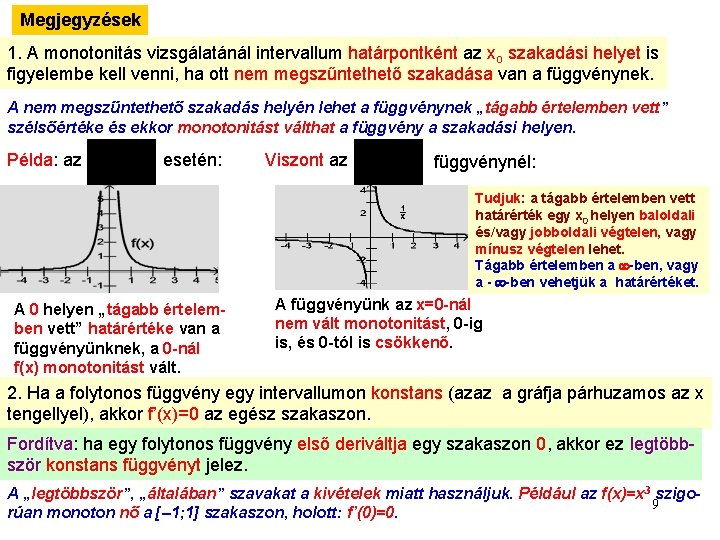
Megjegyzések 1. A monotonitás vizsgálatánál intervallum határpontként az xo szakadási helyet is figyelembe kell venni, ha ott nem megszűntethető szakadása van a függvénynek. A nem megszűntethető szakadás helyén lehet a függvénynek „tágabb értelemben vett” szélsőértéke és ekkor monotonitást válthat a függvény a szakadási helyen. Példa: az esetén: Viszont az függvénynél: Tudjuk: a tágabb értelemben vett határérték egy x 0 helyen baloldali és/vagy jobboldali végtelen, vagy mínusz végtelen lehet. Tágabb értelemben a -ben, vagy a - -ben vehetjük a határértéket. A 0 helyen „tágabb értelemben vett” határértéke van a függvényünknek, a 0 -nál f(x) monotonitást vált. A függvényünk az x=0 -nál nem vált monotonitást, 0 -ig is, és 0 -tól is csökkenő. 2. Ha a folytonos függvény egy intervallumon konstans (azaz a gráfja párhuzamos az x tengellyel), akkor f’(x)=0 az egész szakaszon. Fordítva: ha egy folytonos függvény első deriváltja egy szakaszon 0, akkor ez legtöbbször konstans függvényt jelez. A „legtöbbször”, „általában” szavakat a kivételek miatt használjuk. Például az f(x)=x 3 szigo 9 rúan monoton nő a [– 1; 1] szakaszon, holott: f’(0)=0.

A függvény görbülete, inflexiós pontja A függvény görbületét mindig „alulról nézve” határozzuk meg, a domborút konvexnek, a homorút konkávnak nevezzük. Példa: A felrajzolt függvény az [a; b] szakaszon konkáv (homorú alulról nézve), a [b; c] szakaszon konvex (domború). A Pi pontban a függvény görbülete megváltozik, ezt a pontot inflexiós pontnak nevezzük. A görbület a gráfhoz húzott érintőkkel is meghatározható. Tétel: ha az f(x) függvény az értelmezési tartományának egy szakaszán differenciálható és ezen a szakaszon a derivált függvény növekvő, akkor az f(x) függvény az intervallumon konvex. Ha viszont az f ’(x) derivált függvény csökkenő, akkor az adott szakaszon az f(x) konkáv. „A derivált növekvő” geometriailag azt jelenti, hogy az érintők iránytangensei nőnek. Rajzon: A „lejtős” érintők jobbra haladva „emelkedők” lesznek. Következmény: ha egy intervallumon az f ”(x)>0, akkor az f ’(x) növekvő, tehát az eredeti f(x) konvex. Ha pedig az f ”(x)<0, akkor az f(x) konkáv. 10 Az inflexiós pontban a második derivált előjelet vált, így ott f ”(x 0)=0, de f ’’’(x§) 0.

Példa: adjuk meg az f(x)=x 3/3+x 2– 3 x– 5 inflexiós pontjait, konvex és konkáv szakaszait! Az f(x)-nek abban az xo pontban lehet inflexiós pontja, ahol f ”(xo)=0. Ebben az xo pontban akkor van inflexiós pont, ha f ”’(xo) 0. (Ha létezik az f ’’’(xo). ) Szükség van az első és a második deriváltra: f ’(x)=x 2+2 x– 3 és f ”(x)=2 x+2. Ha f ”(x)=2 x+2=0, akkor x=– 1. A harmadik derivált: f ”’(x)=2 0, így x=– 1 -nél f(x)-nek inflexiós pontja van. A függvényérték itt: – 7/3 , tehát Pi(– 1; – 7/3 ). A görbületi szakaszok: az f ”(x)>0, ha 2 x+2>0, azaz x>– 1. Ha x<– 1, akkor f ”(x)<0. A függvényünk tehát a ]– ; – 1] intervallumon konkáv, a [– 1; [ szakaszon konvex. Példa: adjuk meg a monotonitás szempontjából már vizsgált függvény inflexiós pontjait. A második derivált: Inflexiós pont ott lehet, ahol f ”(x)=0. Megoldandó: 2 x 4– 5 x 2+1=0. Innen: A gyökök: x 1=– 1, 51; x 2=– 0, 47; x 3=0, 47 és x 4=1, 51. Belátható, hogy a harmadik derivált egyik pontban sem 0 (azaz f”’(xi) 0), így négy inflexiós pont van. 11 A függvény gráfját már láthattuk.

Megjegyzések 1. A függvény nem megszűntethető szakadási helye lehet tágabb értelemben vett inflexiós pont (görbületváltási hely). Példa: az görbületeit vizsgáljuk. Ehhez: Az f ”(x)<0, ha x<0, azaz a ]– ; 0[ intervallumon a függvény konkáv és f ”(x)>0, ha x>0, azaz nullától jobbra a függvény végig konvex. 2. Szoktunk beszélni tágabb értelemben vett görbületről: egy függvény tágabb értelemben konvex, ha az adott szakaszon nem konkáv. Példa: vizsgáljuk meg görbület szempontjából a következő függvényt: Az abszolútérték függvényt átírhatjuk abszolút érték mentes alakba, így az ábrázolás egyszerűbb lehet. A függvény képe: A függvény tágabb értelemben konvex, hiszen a töréspontok kivételével f ”(x) 0. 12

3. Határérték számolás különleges esetekben A bonyolultabb határérték számításokhoz gyakran trükköket kell kitalálnunk. A l’Hospital szabály alkalmazása ezt elkerülhetővé teheti. A l’Hospital szabály Ha az függvény helyettesítési értéke az xo helyen alakú, akkor: Vigyázat: nem a törtet kell deriválni! Példa: adjuk meg az határértékét az 1, a 2, a 3 helyeken, illetve a -ben! A kifejezést tekinthetjük racionális törtfüggvénynek, amely – 3 és 3 kivételével folytonos, így: (a számláló és a nevező helyettesítési értéke is 0, így a l’Hospital szabály alkalmazható) (a számláló és a nevező helyettesítési értéke is , így a l’Hospital szabály alkalmazható) A szabályt mégegyszer alkalmaztuk. A l’Hospital szabály a határérték számolásra csak az adott feltételekkel használható! 13

Példa: A feladatban tulajdonképpen az exponenciális és a hatványfüggvény „növekedési sebességét” hasonlítjuk össze. A l’Hospital szabály alkalmazható, hiszen a helyettesítési érték: Az ex minden deriváltja önmaga, az xk k-adik deriváltja k!, ami konstans. Tehát az exponenciális függvény „dominánsabb” a hatványfüggvénynél. 4. „Bonyolultabb” függvények közelítése hatványfüggvényekkel A függvények sorfejtése Tétel: ha az f(x) függvény tetszőlegesen sokszor deriválható, akkor az hatványsort az f(x) függvény xo-hoz tartozó Taylor sorának nevezzük. Ha az xo=0, akkor a sort Mac. Laurin sornak nevezzük. Tehát az f(x) Mac. Laurin sora: Ezek a formulák teszik lehetővé a „bonyolult” függvények közelítését egyszerű hatványfüggvényekkel. 14

Példa: írjuk fel az f(x)=sinx Mac. Laurin sorát. A deriváltak helyettesítési értékeit külön kiszámoljuk: f(0)=sin 0=0. f””(x)=sinx f ’(x)=cosx f ’(0)=1. f ’’(x)=–sinx f ’’(0)=0. f ’’’(x)=–cosx f’’’(0)=– 1. f””(0)=0, és minden kezdődik elölről. Helyettesítünk a Mac. Laurin sor képletébe: Tehát a sinx Mac. Laurin sora: Ha ábrázoljuk az függvényt (a sorfejtésnek az első 3 tagját vesszük): Láthatjuk, hogy a szakaszon ez a függvény jól közelíti a sinx függvényt. Pontos formulák léteznek a közelítés hibájának megadására. Ha nem a nulla környezetében (Mac. Laurin sor) akarjuk közelíteni a függvényt, hanem tetszőleges xo-nál, akkor az általánosabb Taylor sort használjuk. Hasonlóan egyszerűen levezethető, érdemes (célszerű) „fejből” tudni a következőket: Az lnx függvény hatványsorát (mivel a függvénynek és deriváltjának a 0 helyen nincs helyettesítési értéke) valamely pozitív xo helyen képezzük. 15 A fejezet tárgyalását befejeztük.