8 7 Indeterminate Forms LHpitals Rule Actually LHpitals

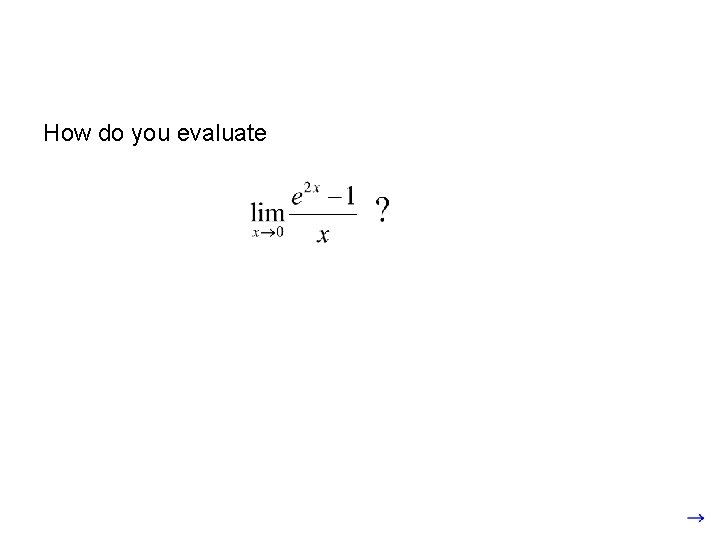
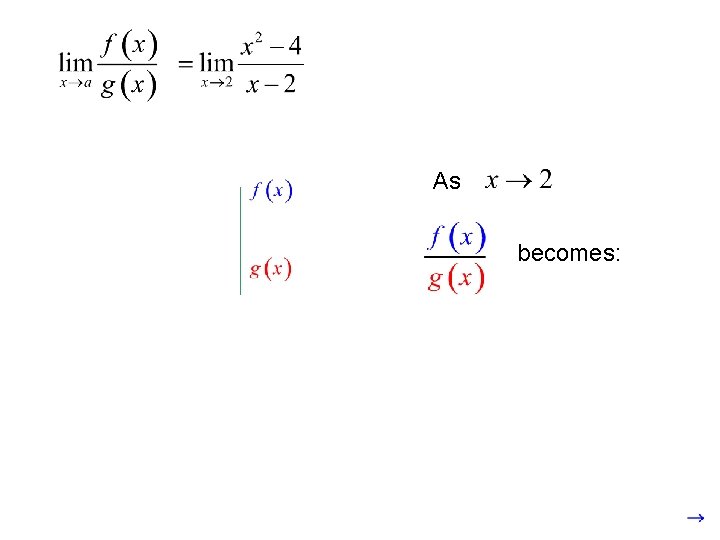
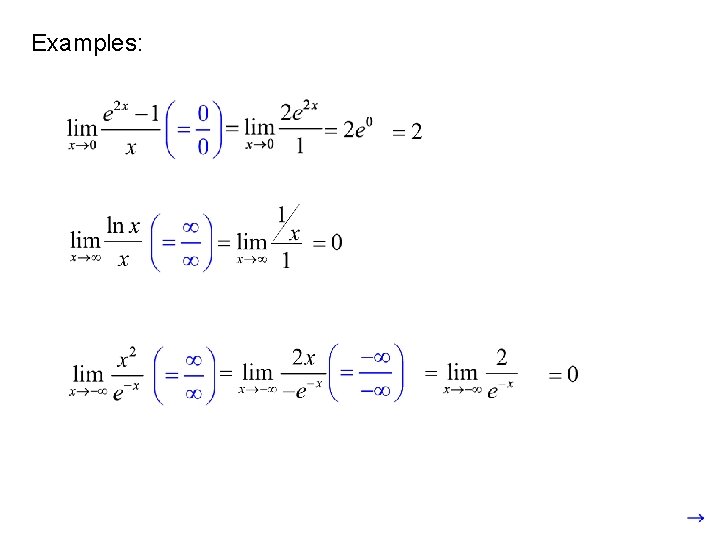
  • Slides: 23
Download presentation
8. 7 Indeterminate Forms & L’Hôpital’s Rule Actually, L’Hôpital’s Rule was developed by his

8. 7 Indeterminate Forms & L’Hôpital’s Rule Actually, L’Hôpital’s Rule was developed by his teacher Johann Bernoulli. De l’Hôpital paid Bernoulli for private lessons, and then published the first Calculus book based on those lessons. Guillaume De l'Hôpital 1661 - 1704 Greg Kelly, Hanford High School, Richland, Washington

7. 7 L’Hôpital’s Rule Johann Bernoulli 1667 - 1748

7. 7 L’Hôpital’s Rule Johann Bernoulli 1667 - 1748

Objectives • Recognize limits that produce indeterminate forms. • Apply L’Hôpital’s Rule to evaluate

Objectives • Recognize limits that produce indeterminate forms. • Apply L’Hôpital’s Rule to evaluate a limit.

How do you evaluate

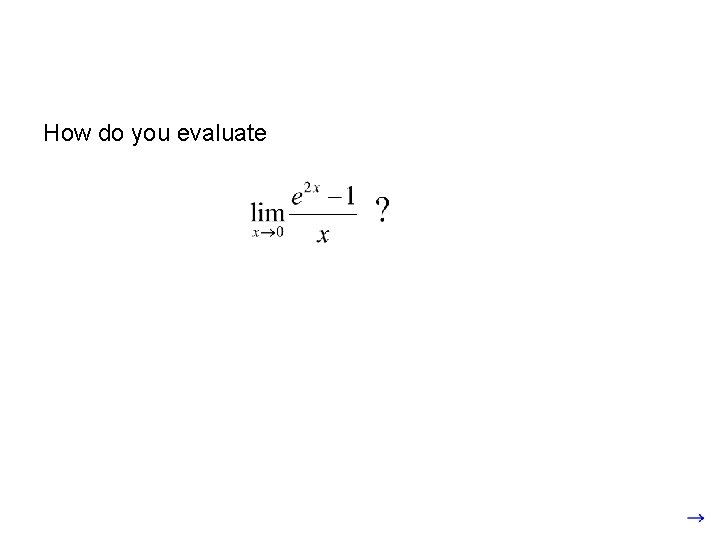
How do you evaluate

L’Hôpital’s Rule: (Theorem 7. 4 on page 531) Let f and g be functions

L’Hôpital’s Rule: (Theorem 7. 4 on page 531) Let f and g be functions that are differentiable on an open interval (a, b) containing c, except possibly at c itself. If the limit of f(x) / g(x) as x approaches c produces the indeterminate form 0 / 0 then provided the limit on the right exists (or is infinite).

L’Hôpital’s Rule also applies if the limit of f(x) / g(x) as x approaches

L’Hôpital’s Rule also applies if the limit of f(x) / g(x) as x approaches c produces any one of the indeterminate forms (If 0 / 0 or some kind of ∞ / ∞, then

Consider: If we try to evaluate this by direct substitution, we get: Zero divided

Consider: If we try to evaluate this by direct substitution, we get: Zero divided by zero can not be evaluated, and is an example of indeterminate form. In this case, we can evaluate this limit by factoring and canceling:

The limit is the ratio of the numerator over the denominator as x approaches

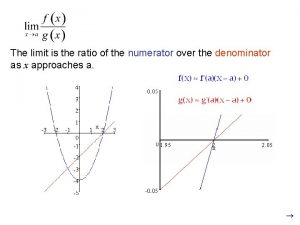
The limit is the ratio of the numerator over the denominator as x approaches 2. If we zoom in far enough, the curves will appear as straight lines.

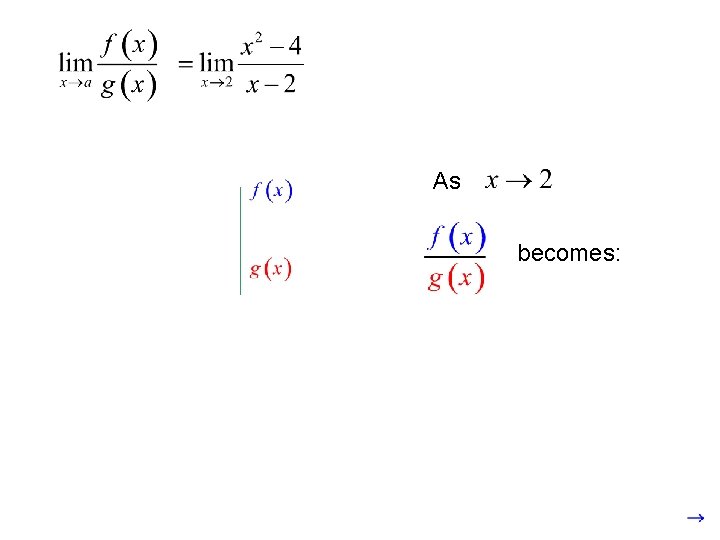
As becomes:

As becomes:

As becomes:

As becomes:

L’Hôpital’s Rule: If is indeterminate, then:

L’Hôpital’s Rule: If is indeterminate, then:

We can confirm L’Hôpital’s rule by working backwards, and using the definition of derivative:

We can confirm L’Hôpital’s rule by working backwards, and using the definition of derivative:

Examples:

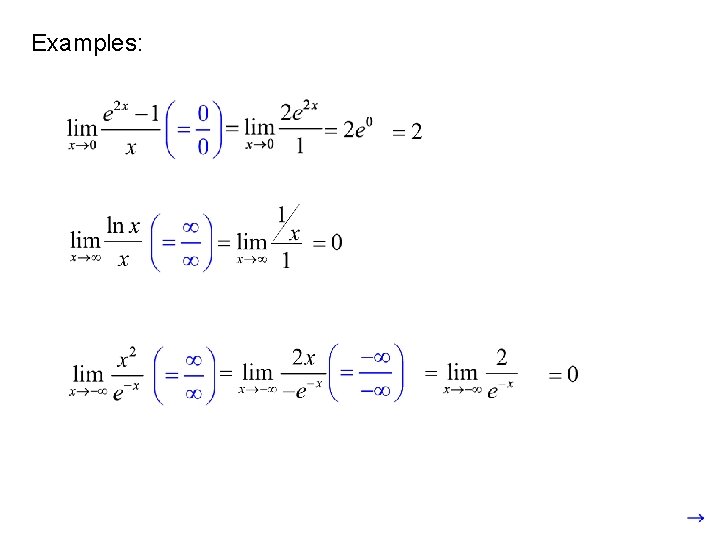
Examples:

Other indeterminate forms: To use L'Hôpital's Rule, you must have

Other indeterminate forms: To use L'Hôpital's Rule, you must have

Examples:

Examples:

Example: If it’s no longer indeterminate, then STOP! If we try to continue with

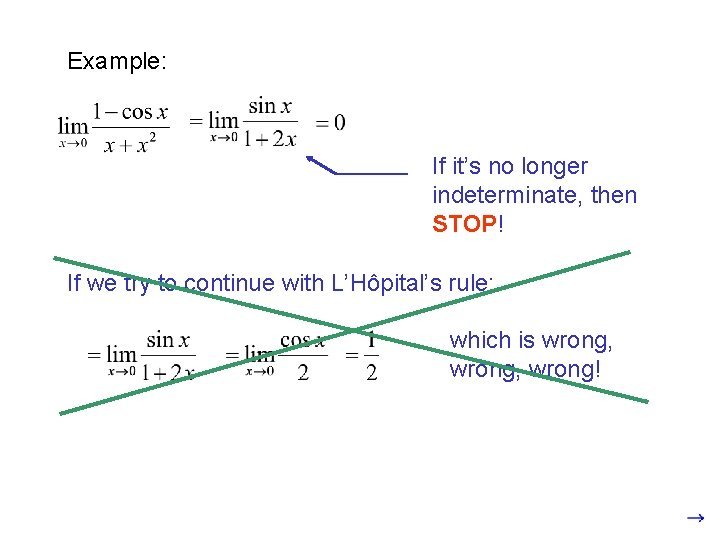
Example: If it’s no longer indeterminate, then STOP! If we try to continue with L’Hôpital’s rule: which is wrong, wrong!

On the other hand, you can apply L’Hôpital’s rule as many times as necessary

On the other hand, you can apply L’Hôpital’s rule as many times as necessary as long as the fraction is still indeterminate: (Rewritten in exponential form. ) not

This is indeterminate form If we find a common denominator and subtract, we get:

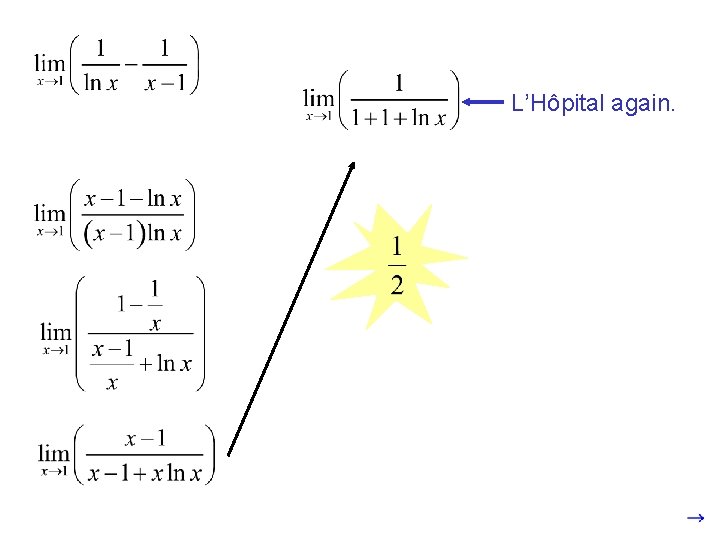
This is indeterminate form If we find a common denominator and subtract, we get: Now it is in the form L’Hôpital’s rule applied once. Fractions cleared. Still

L’Hôpital again.

L’Hôpital again.

Indeterminate forms: Determinate Forms

Indeterminate forms: Determinate Forms

Homework 8. 7 (page 576) #5 – 15 odd 19, 21, 35 – 39

Homework 8. 7 (page 576) #5 – 15 odd 19, 21, 35 – 39 odd, 49 p