2 Differentiation Copyright Cengage Learning All rights reserved

2 Differentiation Copyright © Cengage Learning. All rights reserved. 1

2. 8 Related Rates Copyright © Cengage Learning. All rights reserved.

Objectives Examine related variables. Solve related-rate problems. 3

Related Variables 4

Related Variables In this section, you will study problems involving variables that are changing with respect to time. If two or more such variables are related to each other, then their rates of change with respect to time are also related. For instance, suppose that x and y are related by the equation y = 2 x. 5

Related Variables If both variables are changing with respect to time, then their rates of change will also be related. In this simple example, you can see that because y always has twice the value of x, it follows that the rate of change of y with respect to time is always twice the rate of change of x with respect to time. 6

Example 1 – Examining Two Rates That Are Related The variables x and y are differentiable functions of t and are related by the equation y = x 2 + 3. When x = 1, dx/dt = 2. Find dy/dt when x = 1. Solution: Use the Chain Rule to differentiate both sides of the equation with respect to t. 7

Example 1 – Solution cont’d When x = 1 and dx/dt = 2, you have 8

Solving Related-Rate Problems 9

Example 2 – Changing Area A pebble is dropped into a calm pool of water, causing ripples in the form of concentric circles, as shown in the photo. Total area increases as the outer radius increases. The radius r of the outer ripple is increasing at a constant rate of 1 foot per second. When the radius is 4 feet, at what rate is the total area A of the disturbed water changing? 10

Example 2 – Solution The variables r and A are related by the equation for the area of a circle, A = r 2. To solve this problem, use the fact that the rate of change of the radius is constant at 1 foot per second. So, dr/dt = 1. Equation: Given rate: Find: 11

Example 2 – Solution cont’d Using this information, you can proceed as in Example 1. 12

Example 2 – Solution cont’d When r = 4 and dr/dt = 1, you have When the radius is 4 feet, the area is changing at a rate of 8 square feet per second. 13

Guidelines for Solving Related Rates Problems 1. 2. Draw a picture and name the variables and constants. Use t for time. Write down the numerical information (in terms of the symbols you have chosen) 3. Write down what we are asked to find (usually a rate, expressed as a derivative) 4. Write an equation involving the variables whose rates of change either are given or are to be determined. You will likely use: • a simple geometric fact (like the relation between a sphere’s volume and its radius, or the relation between the volume of a cylinder and its height); or • a trigonometric function (like tan�� = opposite/adjacent); or • similar triangles; or • the Pythagorean theorem. 5. Using the Chain Rule, differentiate with respect to t. 6. Substitute into the resulting equation all known values for the variables and their rates of change. 7. Solve for the required rate of change. CAUTION: DO NOT PLUG IN VALUES OF VARIABLES UNTIL AFTER DIFFERENTIATING 14

Solving Related-Rate Problems In Step 4 of the guidelines, note that you must write an equation that relates the given variables. To help you with this step, reference tables that summarize many common formulas are included in the appendices. For instance, the volume of a sphere of radius r is given by the formula. 15

Solving Related-Rate Problems The table below lists examples of the mathematical models for some common rates of change that can be used in the first steps of the solution of a related-rate problem. 16

Truck Problem Truck A travels east at 40 mi/hr. Truck B travels north at 30 mi/hr. How fast is the distance between the trucks changing 6 minutes later? 17

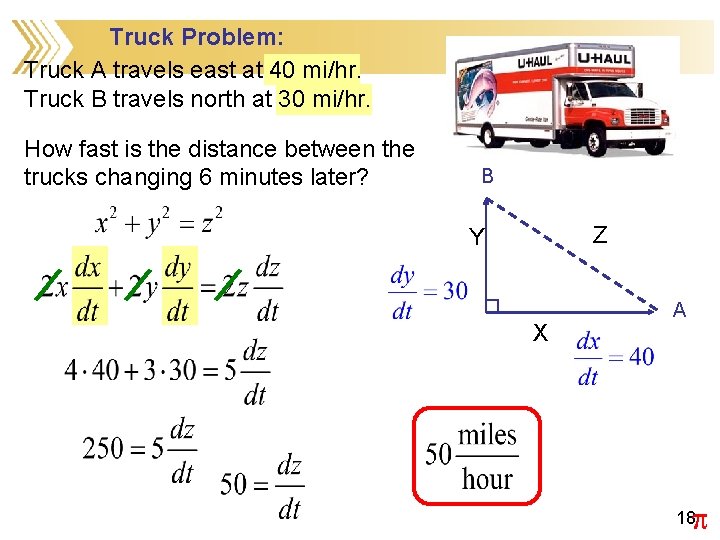
Truck Problem: Truck A travels east at 40 mi/hr. Truck B travels north at 30 mi/hr. How fast is the distance between the trucks changing 6 minutes later? B Z Y X A p 18

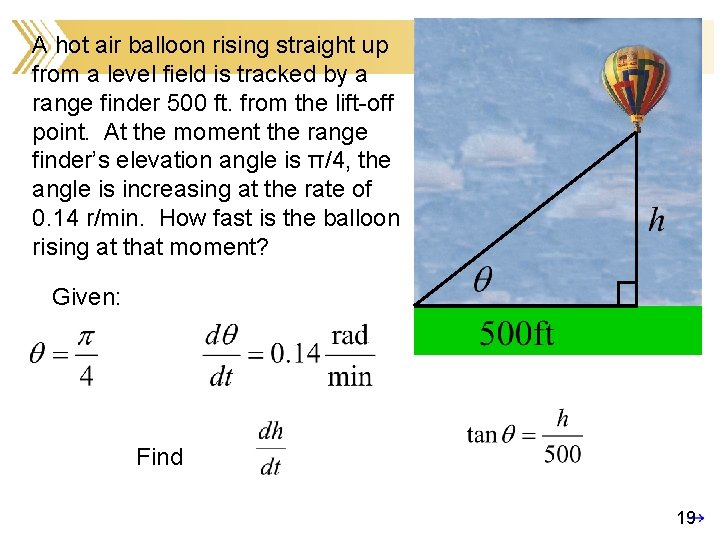
A hot air balloon rising straight up from a level field is tracked by a range finder 500 ft. from the lift-off point. At the moment the range finder’s elevation angle is π/4, the angle is increasing at the rate of 0. 14 r/min. How fast is the balloon rising at that moment? Given: Find 19

Hot Air Balloon Problem: Given: How fast is the balloon rising? Find 20

Give it a Try! A 20 foot ladder leans against a vertical wall. If the bottom of the ladder slides away at a rate of 2 ft/sec, how fast is the ladder sliding down the wall when the top of the ladder is 12 feet above the ground? 20 y x 21

Example 4 – Increasing Production A company is increasing the production of a product at the rate of 200 units per week. The weekly demand function is modeled by p = 100 – 0. 001 x where p is the price per unit (in dollars) and x is the number of units produced in a week. Find the rate of change of the revenue (in dollars) with respect to time (in weeks) when the weekly production is 2000 units. Is the rate of change of the revenue greater than $20, 000 per week? 22

Example 4 – Solution Because production is increasing at a rate of 200 units per week, you know that at time t the rate of change is dx/dt = 200. So, the problem can be stated as shown. Given rate: Find: 23

Example 4 – Solution cont’d To find the rate of change of the revenue, you must find an equation that relates the revenue R and the number of units produced x. Equation: By differentiating both sides of the equation with respect to t, you obtain 24

Example 4 – Solution cont’d When x = 2000 and dx/dt = 200, the rate of change of the revenue is So, the rate of change of the revenue is not greater than $20, 000 per week. 25