2 Arreglos e invariantes Arreglos Un arreglo es

2. Arreglos e invariantes

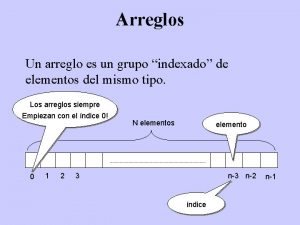
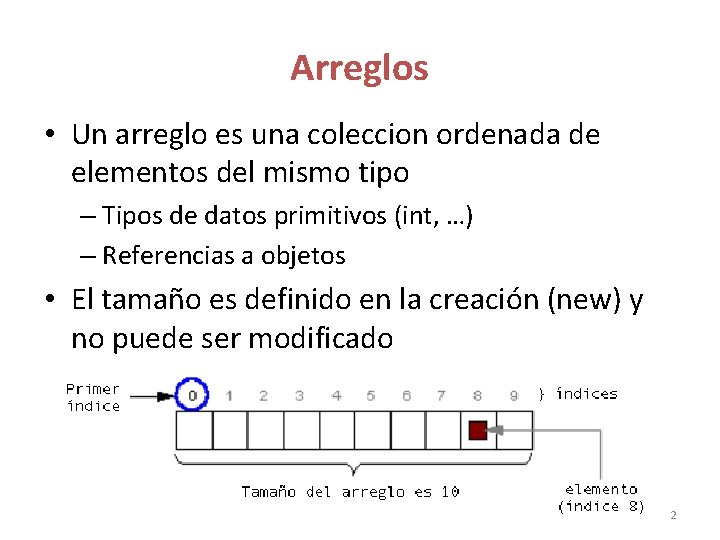
Arreglos • Un arreglo es una coleccion ordenada de elementos del mismo tipo – Tipos de datos primitivos (int, …) – Referencias a objetos • El tamaño es definido en la creación (new) y no puede ser modificado 2

Arreglos de Tipos Primitivos int[] x; // equivalente a int x[] x = new int[3]; x[0] = 10; x[1] = 20; x[2] = 30; X 10 20 30 Nota: x. length es una variable final que entrega el tamaño del arreglo 3

Arreglos de Arreglos • Java permite crear arreglos de arreglos con la siguiente sintaxis int[][] matriz = new int[4][]; for (int i = 0; i < matriz. length; i++) { matriz[i] = new int[5]; for (int j = 0; j < matriz[i]. length; j++) { matriz[i][j] = i + j; } } 4

Inicialización de Arreglos • Un arreglo puede inicializarse con la siguiente sintaxis: boolean[] respuestas = {true, false, true}; String[] nombres = {"Ana María", "Carlos"}; String[][] humor = { { "Coco Legrand", "Alvaro Salas" }, { "Les Luthiers" }, { "Groucho Marx", "Buster Keaton", "Jerry Lewis", "Woody Allen" } }; 5

Ejemplo: Búsqueda del máximo Estrategia: revisar todos los elementos a[0] hasta a[n-1] y registrar el mayor visto hasta ahora en m Para estrategia el invariante puede ser el siguiente m = max(a[0] … a[k]), 1 <= k<n a 0 a 1 . . . ai k . . . an-1

El invariante de una iteración Invariante: Condición (conjunto) que describe lo que un ciclo hace. Permanece invariante: antes, en cada iteración y al final. Debería representar la estrategia que se usa para resolver el problema. Se usa para: A partir del invariante desarrollar el trozo de programa seguro Demostrar que el trozo programa hace lo queremos Explicar un trozo de programa Al escribir un ciclo con invariante se debe a) establecer la validez inicial del invariante, con instrucciones de inicialización. b) avanzar hacia un estado final. c) cada iteración debe preservar la validez del invariante.

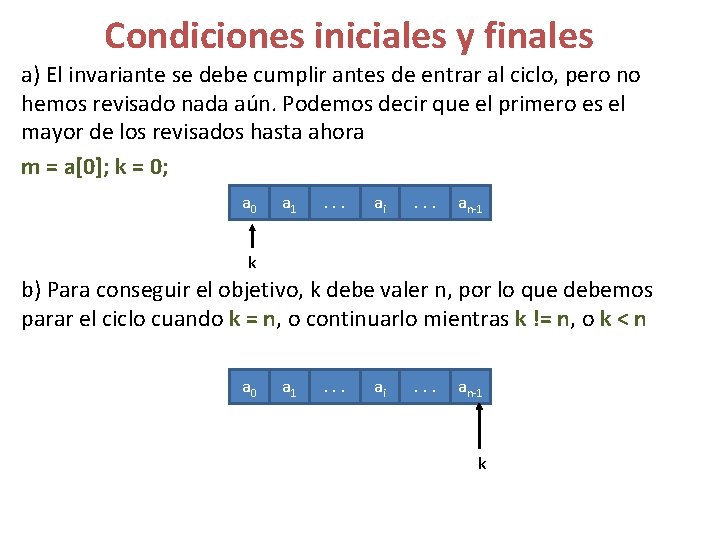
Condiciones iniciales y finales a) El invariante se debe cumplir antes de entrar al ciclo, pero no hemos revisado nada aún. Podemos decir que el primero es el mayor de los revisados hasta ahora m = a[0]; k = 0; a 0 a 1 . . . ai . . . an-1 k b) Para conseguir el objetivo, k debe valer n, por lo que debemos parar el ciclo cuando k = n, o continuarlo mientras k != n, o k < n a 0 a 1 . . . ai . . . an-1 k

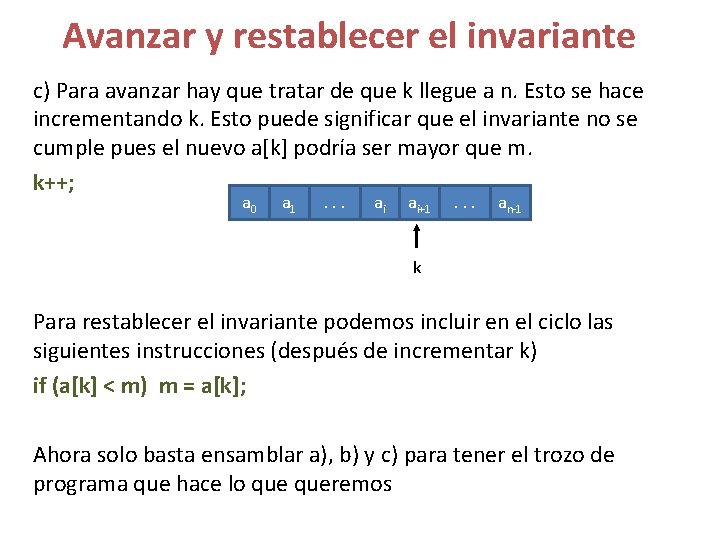
Avanzar y restablecer el invariante c) Para avanzar hay que tratar de que k llegue a n. Esto se hace incrementando k. Esto puede significar que el invariante no se cumple pues el nuevo a[k] podría ser mayor que m. k++; a 0 a 1 . . . ai ai+1 . . . an-1 k Para restablecer el invariante podemos incluir en el ciclo las siguientes instrucciones (después de incrementar k) if (a[k] < m) m = a[k]; Ahora solo basta ensamblar a), b) y c) para tener el trozo de programa que hace lo queremos

Ejemplo 1: ordenación por selección Idea: Hacer pasadas sucesivas sobre los datos, se encuentra el máximo del arreglo, y se lo lleva al extremo derecho. Una vez hecho esto, ese elemento deja de ser considerado, porque se encuentra ya en su posición definitiva. Esto conduce al siguiente invariante: • a[i] < a[i+1] para i = k hasta n-1 • a[j] < a [i] con j = 0 hasta k-1, todos desordenados En palabras: "Los elementos desde k hasta n-1 ya están ordenados y son mayores que los primeros k".

Condiciones iniciales y finales a) Condiciones iniciales: al principio no se puede decir nada, por lo que se hace k = n, lo que dice que implica: • a[i] < a[i+1] para i = n hasta n-1 (no existe elemento) • a[j] < a [n] con j = 0 hasta n-1, todos desordenados (a[n] no existe) ¿Más intuitivo? : al principio poner el mayor del arreglo en el lugar n -1 y hacer k = n-1 b) Condición final: k = 1 (o mientras k >= 2) • a[i] < a[i+1] para i = 1 hasta n-1 • a[j] < a [1] con j = 0 hasta 0, todos desordenados

Ord. x selección: avanzar y restablecer invariante // Ordenar a[0], . . . , a[n-1] por selección k = n; // inicialmente los n primeros están desordenados while( k>1 ) { --k; //acercar k a la meta, se rompe el invariante Llevar el max de a[0], . . . , a[k] hacia a[k]; //esto restablece el invariante } Donde Llevar el max de a[0], . . . , a[k] hacia a[k] => i = 0; // a[i] es el max hasta el momento for( j=1; j<=k; ++j ) if( a[j]>a[i] ) i = j; // ahora intercambiamos a[i] con a[k] t = a[i]; a[i] = a[k]; a[k] = t;

Ejemplo 2: ordenación por inserción Este algoritmo va construyendo un trozo ordenado del arreglo al extremo izquierdo, y en cada iteración le agrega un nuevo elemento a ese grupo. Invariante: • a[i] < a[i+1] para i = 0 hasta k-1 • a[k] hasta a[n-1] desordenados En palabras: "Los elementos desde 0 hasta k-1 ya están ordenados y los siguientes desordenados".

Condiciones iniciales y finales a) Condiciones iniciales: al principio se puede decir que el primer elemento a[0] está ordenado por definición, por lo que se hace k = 1, lo que implica: • a[i] < a[i+1] para i = 0 hasta 1 -1 • a[1] hasta a[n-1] desordenados b) Condición final: k = n (o mientras k < n) • a[i] < a[i+1] para i = 0 hasta n-1 • a[n] hasta a[n-1] desordenados (no existe!)

Avanzar y restablecer invariante // Ordenar a[0], . . . , a[n-1] por inserción k = 0; // inicialmente el primer elemento esta ordenado while( k < n ) { ++k; //acercar k a la meta, se rompe el invariante Insertar a[k-1] entre a[0], . . . , a[k-2]; //esto restablece el invariante } Donde Insertar a[k-1] entre a[0], . . . , a[k-2] => for( j=k-1; j>0 && a[j-1]>a[j]; --j ) { // intercambiar a[j-1] con a[j] t = a[j]; a[j] = a[j-1]; a[j-1] = t; }

Optimización En vez de ir “corriendo” el elemento a insertar en cada paso mejor vamos corriendo los elementos hasta encontrar el lugar apropiado. Así, se puede evitar varias asignaciones, reemplazándolas por una sola al final del ciclo: Insertar a[k-1] entre a[0], . . . , a[k-2] => // versión optimizada t = a[k]; for( j=k; j>0 && a[j-1]>t; --j ) a[j] = a[j-1]; a[j] = t;

Versión final optimizada (y algo variada) // Ordenar a[0], . . . , a[n-1] por inserción k = 1; // inicialmente primer elemento ordenado while( k < n ) { // Insertar a[k] entre a[0], . . . , a[k-1] t = a[k]; for( j=k; j>0 && a[j-1]>t; --j ) a[j] = a[j-1]; a[j] = t; ++k; }

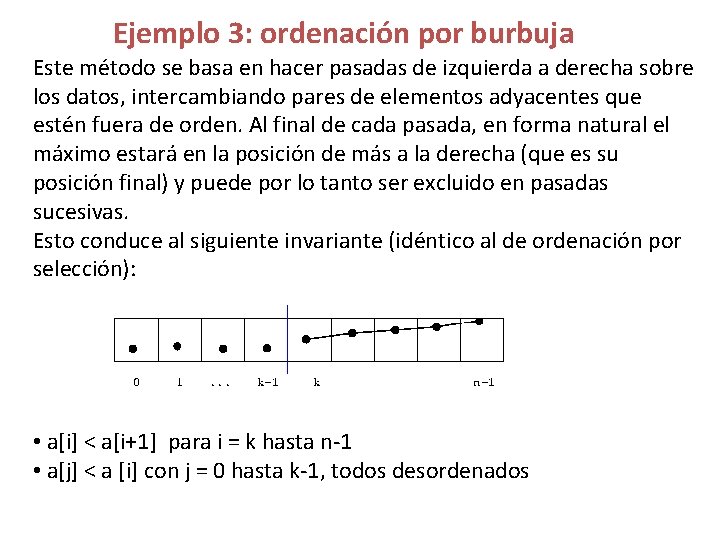
Ejemplo 3: ordenación por burbuja Este método se basa en hacer pasadas de izquierda a derecha sobre los datos, intercambiando pares de elementos adyacentes que estén fuera de orden. Al final de cada pasada, en forma natural el máximo estará en la posición de más a la derecha (que es su posición final) y puede por lo tanto ser excluido en pasadas sucesivas. Esto conduce al siguiente invariante (idéntico al de ordenación por selección): • a[i] < a[i+1] para i = k hasta n-1 • a[j] < a [i] con j = 0 hasta k-1, todos desordenados

Ord. X burbuja: avanzar y restablecer invariante // Ordenar a[0], . . . , a[n-1] por la burbuja (borrador) k = n; while( k>1 ) { Hacer una pasada sobre a[0], . . . , a[k-1]; Disminuir k; } Donde Hacer una pasada sobre a[0], . . . , a[k-1] => for( j=0; j<=k-2; ++j ) if( a[j]>a[j+1] ){ // Intercambiar a[j] con a[j+1] t = a[j]; a[j] = a[j+1]; a[j+1] = t; } y Disminuir k =>--k;

Ord. X burbuja: eficiencia Disminuir k => --k; • Si el arreglo está inicialmente ordenado, el programa igual hace n pasadas. • Después de la primera se puede verificar que ya estaba ordenado. • Para aprovechar cualquier posible orden previo, se puede “recordar” el lugar en donde se produjo el último intercambio. • Si una variable i define que el último intercambio en una pasada dada fue entre a[i-1] y a[i], entonces todos los elementos desde a[i] en adelante están ya ordenados • k se puede disminuir haciendo que sea igual a i: Hacer una pasada sobre a[0], . . . , a[k-1] => i=0; for( j=0; j<=k-2; ++j ) if( a[j]>a[j+1] ) { t = a[j]; a[j] = a[j+1]; a[j+1] = t; i = j+1; //Recordar el lugar del último intercambio } Disminuir k => k=i;

Ejemplo 4: Xn Cuando n es entero se puede programar una función más eficiente que la que usa java, basada en el cálculo de una serie. public static double power(double x, int n) { // Algoritmo simple int y = 1; for( int j=n; j>0; --j ) y = y*x; return y; } algoritmo O(n), y su invariante se puede escribir como y * xj == xn

Aprovechando el invariante para la eficiencia Es posible encontrar un algoritmo sustancialmente más eficiente de la siguiente manera. public static double power(double x, int n) { int j = n; long z = x; int contador = 0; while (j>1) { if (j%2 == 0){ z = z*z; j = j/2; } else { z = x*z; j = j-1; } } System. out. println(“Resultado = "+z); } con invariante z* xj == xn

Algoritmo algo más eficiente aún Sacando x del invariante public static double power(double x, int n) { int y = 1, z = x; for( int j=n; j>0; --j ) { while( j%2 == 0) { z = z*z; j = j/2; } y = y*z; } Con invariante y * z j = xn

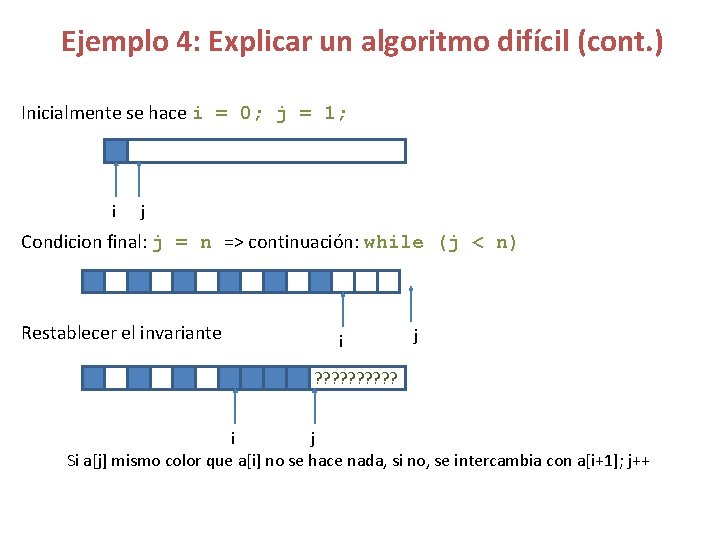
Ejemplo 4: Explicar un algoritmo difícil Se tiene un arreglo con n elementos (a[0] hasta a[n-1]) blanco y negros desordenados. Dejar los elementos intercalados. Si hay mas de una clase que de otra dejarlos todos al final. Ejemplo, si inicialmente se tiene dejarlos invariante ? ? ? i j

Ejemplo 4: Explicar un algoritmo difícil (cont. ) Inicialmente se hace i = 0; j = 1; i j Condicion final: j = n => continuación: while (j < n) Restablecer el invariante i j ? ? ? ? ? i j Si a[j] mismo color que a[i] no se hace nada, si no, se intercambia con a[i+1]; j++

Ejercicio en clases Se tiene un arreglo a[0]. . . a[n-1] con enteros y se quiere particionarlo de modo queden todos los menores que cero a la izquierda y los iguales o mayores que cero a la derecha. En palabras: los elementos anteriores a a[i] son menores que cero, los elementos desde a[i] hasta a[j-1] son mayores que cero y los elementos desde a[j] en adelante son desconocidos <= 0 >0 i desconocidos j