113 CARACTERISTIQUES DINERTIE DES SOLIDES 1 CENTRE DINERTIE









- Slides: 13

1/13 CARACTERISTIQUES D’INERTIE DES SOLIDES 1) CENTRE D’INERTIE 2) MOMENT D’INERTIE 3) MATRICE D’INERTIE 4) SOLIDES ELEMENTAIRES

1) CENTRE D’INERTIE 2/13 a) Définition : On appelle centre d’inertie (ou centre de gravité) d’un solide S le point G, unique et fixe dans S, défini par : intégrale triple Sur l’ensemble du solide S. M est un point « courant » qui décrit totalement le solide S. si solide homogène : centre de masse = centre de volume centre de masse = centre de gravité si g est constant : Habituellement nous « mélangerons » tous ces points… Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

3/13 b) Propriétés : Symétrie matérielle : s’il existe, pour un solide S, un élément de symétrie (plan, axe), d’un point de vue répartition des masses, le centre d’inertie G appartient alors à cet élément de symétrie. Nous sommes très souvent dans cette situation avec un plan de symétrie ou un axe de révolution. Différent d’un axe de symétrie ! Axe de révolution (et de symétrie) Centre d’inertie Axe de symétrie (mais pas de révolution) Moment d’inertie Matrice d’inertie Solides élémentaires

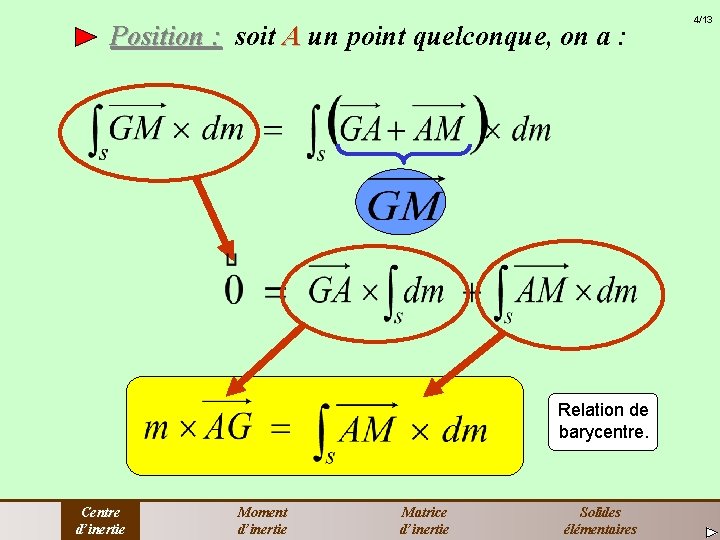
Position : soit A un point quelconque, on a : Relation de barycentre. Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires 4/13

5/13 Nota : si on appelle ( x. G y. G z. G ) les composantes de on a en projection sur les axes du repère : Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

6/13 Associativité : pour un ensemble de n solides Si de masses respectives mi et de centres d’inertie Gi , on a : masse totale Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

1 c) Exemple : Symétrie 2 3 z x. G = 0 y G 3 G 1 O 7/13 G 2 x Par simple associativité, on a : en projection sur y et z ou bien : Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

8/13 Application à un cylindre y Prenons l’élément de matière suivant : R H y dr dy x O r z Préliminaire calcul du volume : H dv = V = Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

9/13 Finalement : Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

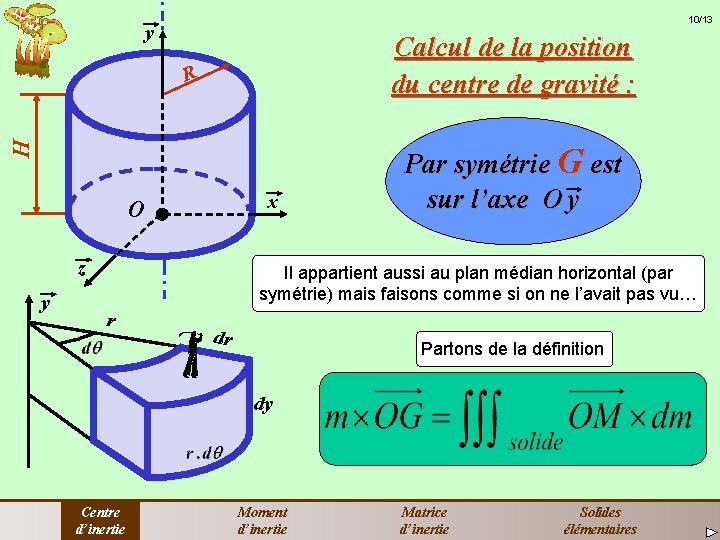
10/13 y Calcul de la position du centre de gravité : H R x O z y Par symétrie G est sur l’axe O y Il appartient aussi au plan médian horizontal (par symétrie) mais faisons comme si on ne l’avait pas vu… r dr Partons de la définition dy Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

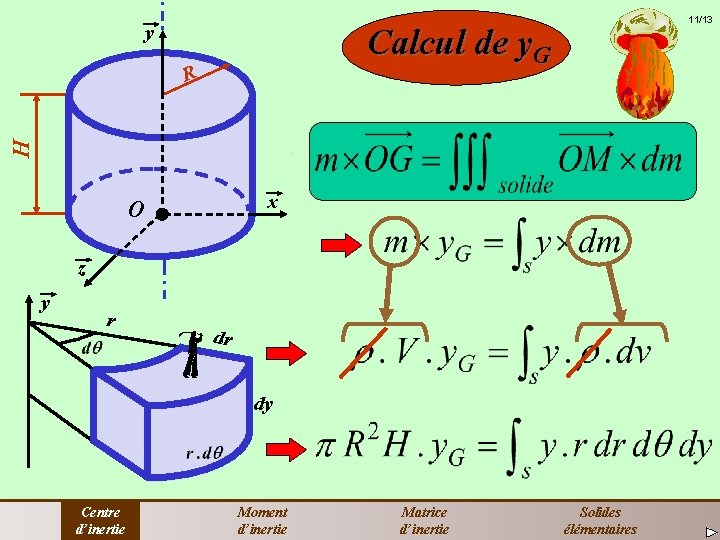
y 11/13 Calcul de y. G H R x O z y r dr dy Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

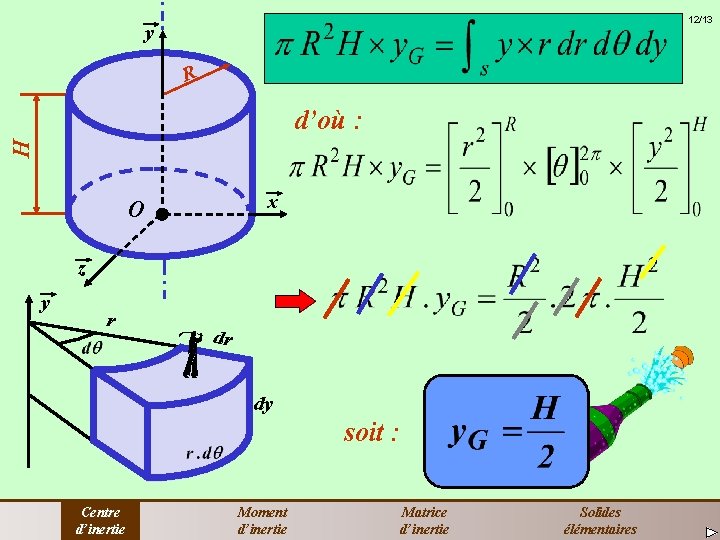
12/13 y R H d’où : x O z y r dr dy soit : Centre d’inertie Moment d’inertie Matrice d’inertie Solides élémentaires

Ce qu’il faut avoir retenu 13/13 (minimum « vital » …) Savoir utiliser les éléments de symétrie pour déterminer un centre de gravité. Connaître la différence entre un axe de symétrie et un axe de révolution. Savoir utiliser l’associativité et la relation de barycentre. Le calcul intégral pour déterminer un centre de gravité n’est pas au programme…
 Mesure de volume des liquides et des corps solides
Mesure de volume des liquides et des corps solides Mesure des liquides
Mesure des liquides Symétrie matérielle
Symétrie matérielle La dilatation des solides
La dilatation des solides Rendement écologique
Rendement écologique Arthropodes caractéristiques
Arthropodes caractéristiques Des des des
Des des des Les corps solides compacts
Les corps solides compacts Les solides pulvérisés
Les solides pulvérisés Solides compacts et divisés
Solides compacts et divisés Solides compacts et divisés
Solides compacts et divisés Differentiate between centre of mass and centre of gravity
Differentiate between centre of mass and centre of gravity Problems on centroid in engineering mechanics
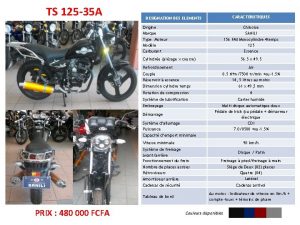
Problems on centroid in engineering mechanics Poids et dimensions des véhicules routiers
Poids et dimensions des véhicules routiers