1 Name two segments whose midpoint is F

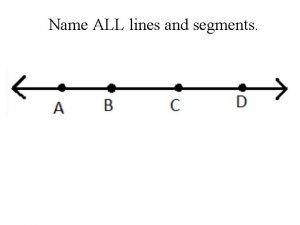
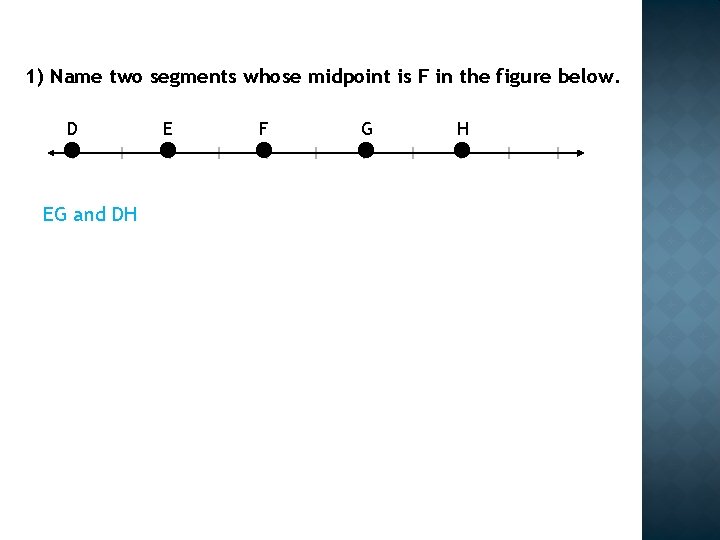
1) Name two segments whose midpoint is F in the figure below. D E F G H 2) Find the coordinates of B is M(-3, 2) is the midpoint of line AB and A is at (-1, -1) 3) Line RS bisects line TU at point Q. Find the value of x and the measure of line QU if TU = 7 x – 5 and TQ = -5 x + 6

1) Name two segments whose midpoint is F in the figure below. D EG and DH E F G H

2) Find the coordinates of B, if M(-3, 2) is the midpoint of line AB and A is at (-1, -1). A and B are on a coordinate plane so use the equation [(x 1 + x 2)/2, (y 1 + y 2)/2]. Let point A be x 1 and y 1 and let point B be x 2 and y 2. (x 1 + x 2)/2 = x-coordinate of the midpoint (-1 + x 2)/2 = -3 -1 + x 2 = -6 x 2 = -5 (y 1 + y 2)/2 = y-coordinate of the midpoint (-1 + y 2)/2 = 2 (-1 + y 2) = 4 y 2 = 3 So point B is at (-5, 3).

3) Line RS bisects line TU at point Q. Find the value of x and the measure of line QU if TU = 7 x – 5 and TQ = -5 x + 6 T Q U Since Q is the midpoint of line TU, we can use the midpoint formula. The midpoint formula tells us that TQ is congruent or equal to QU. So TQ + QU = TU; TQ + TQ = TU or 2(TQ) = TU. 2( TQ) = TU 2(-5 x + 6) = 7 x - 5 -10 x + 12= 7 x - 5 12 = 17 x – 5 17 = 17 x 1=x Plug 1 in for x in the equation for TQ. TQ = -5 x + 6 TQ = -5(1) + 6 TQ = -5 + 6 TQ = 1 = QU

Exploring Angles

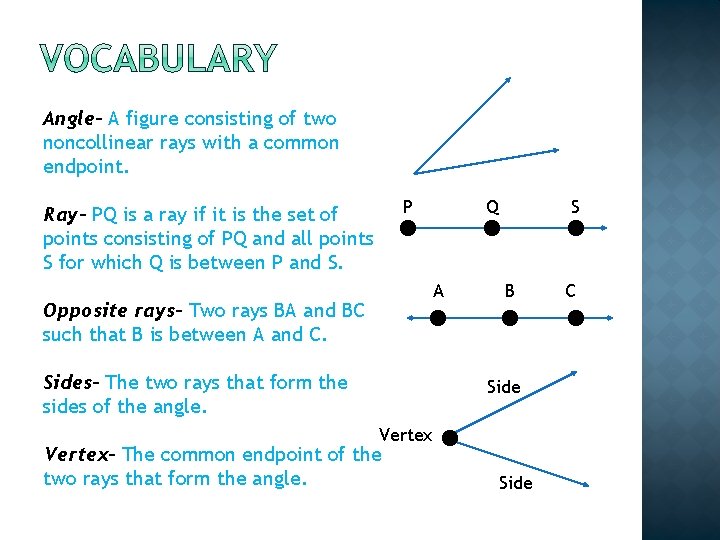
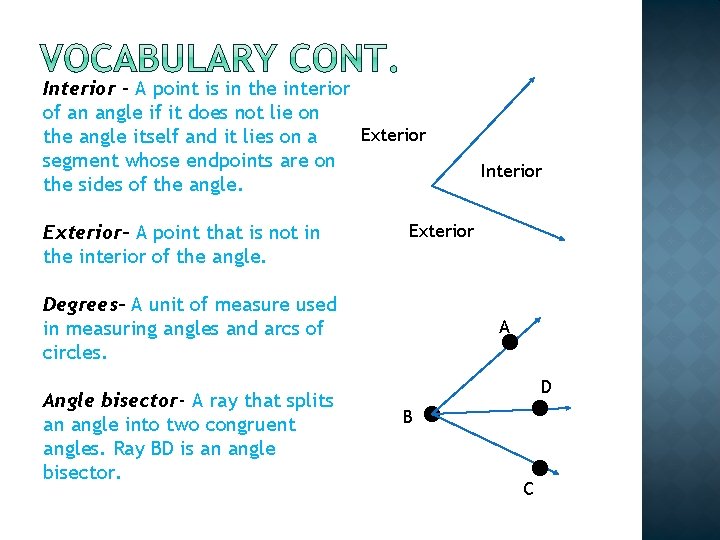
Angle- A figure consisting of two noncollinear rays with a common endpoint. P Ray- PQ is a ray if it is the set of points consisting of PQ and all points S for which Q is between P and S. A Opposite rays- Two rays BA and BC such that B is between A and C. Sides- The two rays that form the sides of the angle. Vertex- The common endpoint of the two rays that form the angle. Q S B Side C

Interior – A point is in the interior of an angle if it does not lie on Exterior the angle itself and it lies on a segment whose endpoints are on Interior the sides of the angle. Exterior- A point that is not in the interior of the angle. Degrees- A unit of measure used A in measuring angles and arcs of circles. D Angle bisector- A ray that splits B an angle into two congruent angles. Ray BD is an angle bisector. C

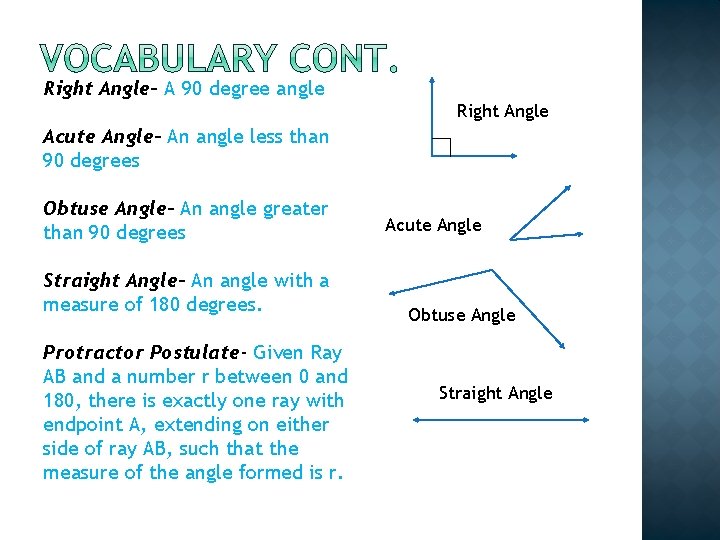
Right Angle- A 90 degree angle Acute Angle- An angle less than 90 degrees Obtuse Angle- An angle greater than 90 degrees Straight Angle- An angle with a measure of 180 degrees. Protractor Postulate- Given Ray AB and a number r between 0 and 180, there is exactly one ray with endpoint A, extending on either side of ray AB, such that the measure of the angle formed is r. Right Angle Acute Angle Obtuse Angle Straight Angle

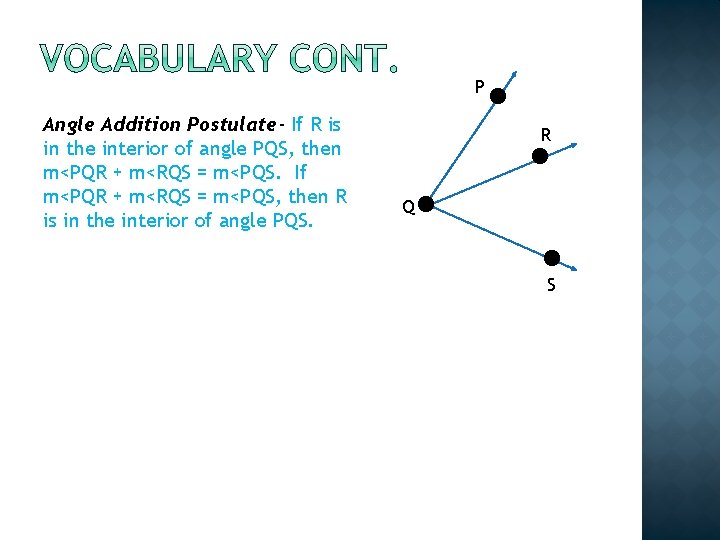
P Angle Addition Postulate- If R is in the interior of angle PQS, then m<PQR + m<RQS = m<PQS. If m<PQR + m<RQS = m<PQS, then R is in the interior of angle PQS. R Q S

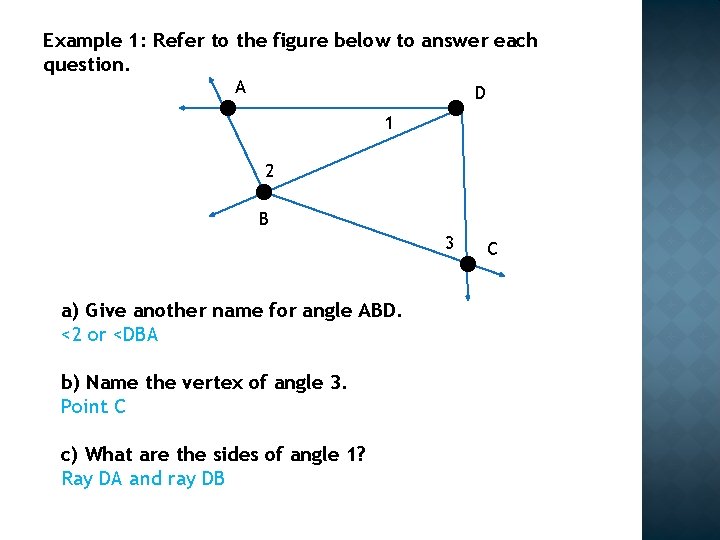
Example 1: Refer to the figure below to answer each question. A D 1 2 B 3 a) Give another name for angle ABD. <2 or <DBA b) Name the vertex of angle 3. Point C c) What are the sides of angle 1? Ray DA and ray DB C

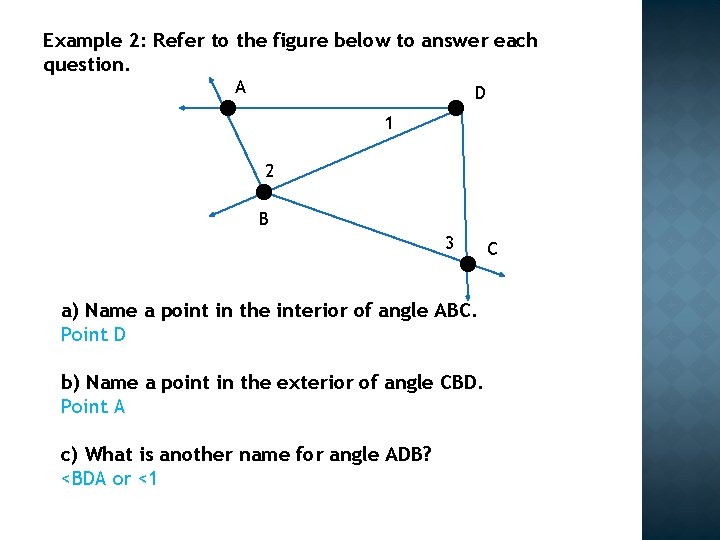
Example 2: Refer to the figure below to answer each question. A D 1 2 B 3 a) Name a point in the interior of angle ABC. Point D b) Name a point in the exterior of angle CBD. Point A c) What is another name for angle ADB? <BDA or <1 C

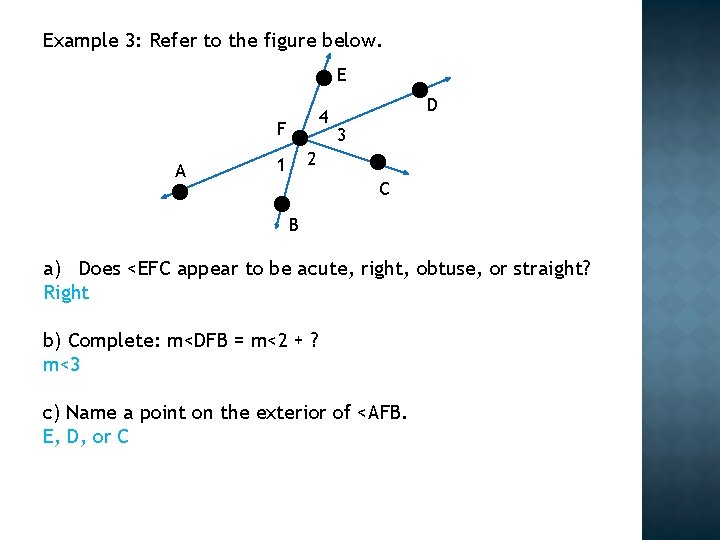
Example 3: Refer to the figure below. E 4 F A D 3 2 1 C B a) Does <EFC appear to be acute, right, obtuse, or straight? Right b) Complete: m<DFB = m<2 + ? m<3 c) Name a point on the exterior of <AFB. E, D, or C

Example 4: Suppose <T is congruent to <S, m<T = 12 n – 6, and m<S = 4 n + 18. Is <T acute, right, obtuse, or straight? m<T = m<S 12 n – 6 = 4 n + 18 8 n – 6 = 18 8 n = 24 n=3 Plug 3 in for n in the equation for m<T = 12 n – 6 m<T = 12(3) – 6 m<T = 36 - 6 m<T = 30 Since 30 is less than 90, angle T is an acute angle.

Example 5: In the figure, ray BA and ray BC are opposite rays, and ray BE bisects <ABD. E D A B C If m<ABE = 6 x + 2 and m<DBE = 8 x -14, find m<ABE. Since ray BE bisects <ABD, we know that m<ABE = m<DBE 6 x + 2 = 8 x -14 2 = 2 x – 14 16 = 2 x 8=x Plug 8 in for x in the equation for m<ABE = 6 x + 2 m<ABE = 6(8) + 2 m<ABE = 48 + 2 m<ABE = 50

Example 6: In the figure, ray BA and ray BC are opposite rays, and ray BE bisects <ABD. E D A B C Given that m<ABD = 2 y and m<DBC = 6 y – 12, find m<DBC. Since ray BA and ray BC are opposite rays, they form a straight angle. m<ABD + m<DBC = 180 2 y + 6 y – 12 = 180 8 y = 192 y = 24 Plug 24 in for y in the equation for m<DBC = 6 y - 12 m<DBC = 6(24) - 12 m<DBC = 144 - 12 m<DBC = 132

Example 7: In the figure, ray BA and ray BC are opposite rays, and ray BE bisects <ABD. E D A B C Find m<EBD if m<ABE = 12 n – 8 and m<ABD = 22 n - 11 Since ray BE bisects <ABD, m<ABE = m<EBD. Use the angle addition postulate m<ABE + m<EBD = m<ABD; 2(m<ABE) = m<ABD 2(12 n – 8) = 22 n -11 24 n – 16 = 22 n -11 2 n – 16 = -11 2 n = 5/2 Plug 5/2 in for n in the equation for m<ABE = 12 n - 8 m<ABE = 12(5/2) - 8 m<ABE = 30 - 8 m<ABE = 22 = m<EBD