1 Lastnosti kontekstno neodvisnih jezikov ODLOITVENE LASTNOSTI ZAPRTJA

1 Lastnosti kontekstno neodvisnih jezikov ODLOČITVENE LASTNOSTI ZAPRTJA

2 Odločitvene lastnosti – povzetek Kot po navadi, bomo, ko bomo govorili o “KNJ”, dejansko mislili na “predstavitev KNJ”: KNS ali SA, ki sprejema na podlagi končnega stanja ali praznega sklada. Obstajajo algoritmi, ki znajo odgovoriti na sledeča vprašanja: 1. Je niz w v kontekstno neodvisnem jeziku L? 2. Je kontekstno neodvisen jezik L prazen? 3. Je kontekstno neodvisen jezik L neskončen?

Neodločljive lastnosti 3 Na mnoga vprašanja, ki smo jih lahko odgovorili za regularne jezike, za KNJ ne moremo. Primer: Sta dva KNJ (v bistvu) isti jezik? Primer: Sta dva KNJ disjunktna (imata prazen presek)? Se še spomnite kako smo na ti dve vprašanji odgovorili za RJ? Potrebovali bomo Turingove stroje in teorijo odločljivosti, da bi dokazali, da ne obstaja algoritem, ki bi odgovoril na zgornji dve vprašanji.

Preverjanje praznosti KNJ Tole smo (v bistvu) že delali. Znamo se znebiti nekoristnih spremenljivk neke KNS … … če je začetni simbol (S) med nekoristnimi spremenljivkami, potem je KNJ, ki ga takšna KNS predstavlja, prazen; v nasprotnem primeru pa ni. 4

Preverjanje članstva v KNJ Izvedeti želimo ali je nek niz w v jeziku L(G). Predpostavili bomo, da je slovnica G v CNF, 5 ali pa jo bomo pretvorili v CNF (če to ni). w = ε bomo obravnavali kot poseben primer, tako da bomo preverili, če je začetni simbol slovnice (S) izničljiv. CYK algoritem je dober primer dinamičnega programiranja – njegova časovna zahtevnost je O(n 3), kjer je n = |w|.

CYK algoritem Naj bo w = a 1…an. Sestavimo n x n “trikotno” matriko množic spremenljivk Xij = {spremenljivka A | A =>* ai…aj}. Indukcija po j–i+1 … … dolžini izpeljanega niza. Končno: “Ali je S v množici X 1 n? ” 6

CYK algoritem – (2) Osnova: Xii = {A | A -> ai je produkcija slovnice}. Indukcija: Xij = {A | obstaja produkcija A -> BC in celo število k, kjer je i < k < j, tako da: B je element Xik in C je element Xk+1, j}. 7

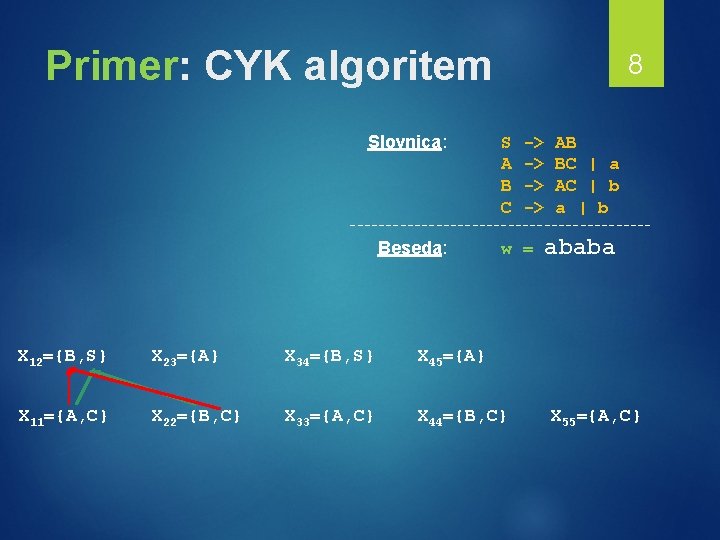
Primer: CYK algoritem Slovnica: 8 S A B C -> -> AB BC | a AC | b a | b --------------------- Beseda: w = X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} ababa X 55={A, C}

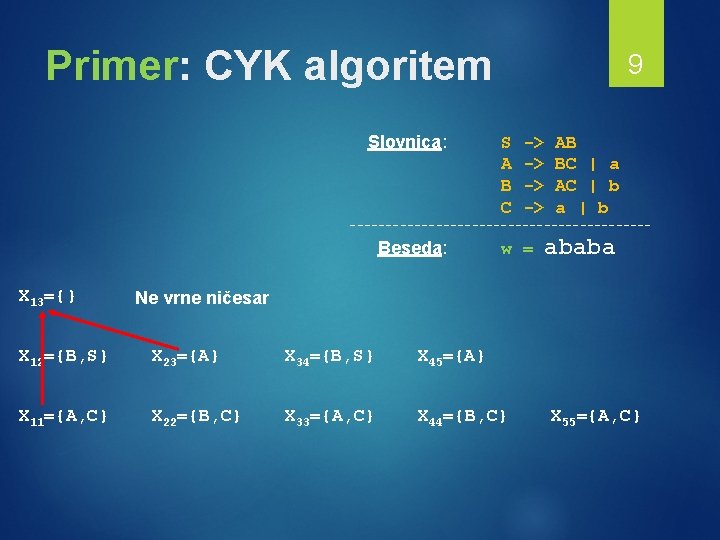
Primer: CYK algoritem Slovnica: 9 S A B C -> -> AB BC | a AC | b a | b --------------------- Beseda: X 13={} w = ababa Ne vrne ničesar X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} X 55={A, C}

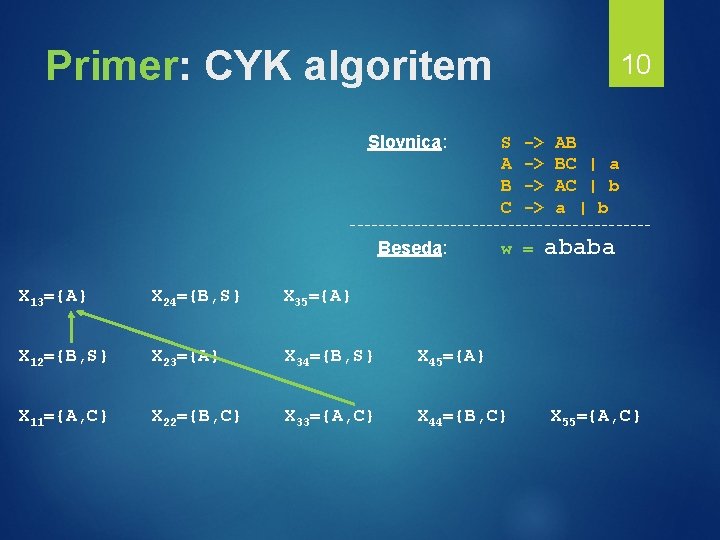
Primer: CYK algoritem Slovnica: 10 S A B C -> -> AB BC | a AC | b a | b --------------------- Beseda: w = X 13={A} X 24={B, S} X 35={A} X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} ababa X 55={A, C}

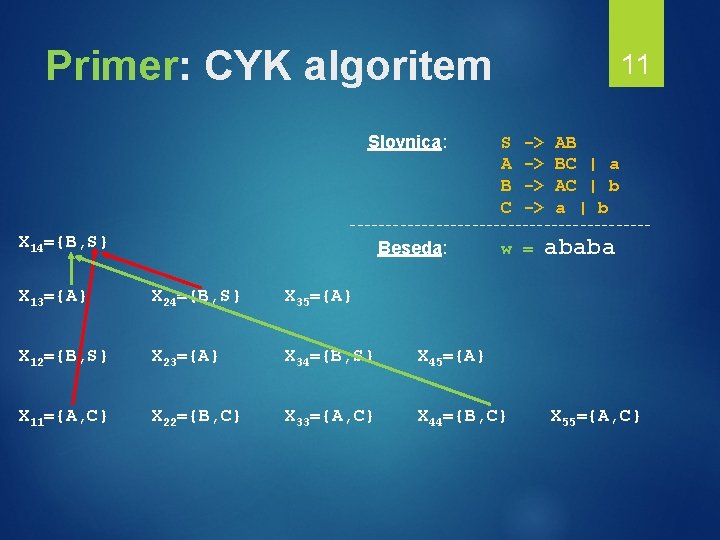
Primer: CYK algoritem Slovnica: 11 S A B C -> -> AB BC | a AC | b a | b --------------------- X 14={B, S} Beseda: w = X 13={A} X 24={B, S} X 35={A} X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} ababa X 55={A, C}

Primer: CYK algoritem S ni v X 15 => w ni v L(G) Slovnica: X 15={A} 12 S A B C -> -> AB BC | a AC | b a | b --------------------- X 14={B, S} X 25={A} X 13={A} X 24={B, S} X 35={A} X 12={B, S} X 23={A} X 34={B, S} X 45={A} X 11={A, C} X 22={B, C} X 33={A, C} X 44={B, C} Beseda: w = ababa X 55={A, C}

Preverjanje neskončnosti 13 Zamisel je podobna kot pri regularnih jezikih. Uporabimo “lemo o napihovanju” z vnaprej določeno konstanto n. Če obstaja niz dolžine med n in 2 n-1, ki je v KNJ, potem je ta KNJ neskončen; drugače ni (je končen).

Lastnosti zaprtja za KNJ so zaprti za unijo, stik in Kleene-ovo ovojnico. KNJ so zaprti tudi za zrcaljenje, homomorfizme in inverzne homomorfizme. KNJ pa niso zaprti za presek in razliko. 14

15 Zaprtje KNJ za unijo Naj bosta L in M dva KNJ s slovnicama G in H (po vrsti). Predpostavimo, da G in H nimata “skupnih” spremenljivk. Imena spremenljivk ne vplivajo na jezik KNS ( ustrezno preimenujemo spremenljivke, če je to potrebno). Naj S 1 in S 2 predstavljata začetna simbola G in H.

Zaprtje KNJ za unijo – (2) Tvorimo novo slovnico za L M tako, da združimo vse spremenljivke in produkcije slovnic G in H, Nato dodamo nov začetni simbol S, Dodamo še produkciji S -> S 1 | S 2. 16

Zaprtje KNJ za unijo – (3) V novi slovnici vse izpeljave začnejo z simbolom S. Prvi korak nato zamenja S z S 1 ali S 2. V prvem primeru (S 1) je rezultat izpeljave niz iz L(G) = L, v drugem primeru (S 2) pa je rezultat izpeljave niz iz L(H) = M. 17

Zaprtje KNJ za stik Naj bosta L in M dva KNJ s slovnicama G in H (po vrsti). Predpostavimo, da G in H nimata “skupnih” spremenljivk. Naj S 1 in S 2 predstavljata začetna simbola G in H. 18

Zaprtje KNJ za stik – (2) Tvorimo novo slovnico za LM tako, da združimo vse spremenljivke in produkcije slovnic G in H, Nato dodamo nov začetni simbol S, Dodamo še produkcijo S -> S 1 S 2. Vsaka izpeljava iz S je niz iz L, ki mu sledi niz iz M. 19

Zaprtje KNJ za Kleene-ovo ovojnico Jezik L predstavimo s slovnico G, ki ima začetni simbol S 1. Novo slovnico za L* tvorimo tako, da slovnici G dodamo nov 20 začetni simbol S ter produkciji S -> S 1 S | ε. Skrajno desna izpeljava iz S generira niz nič ali več (staknjenih) S 1, vsak S 1 pa generira nek niz iz jezika L.

Zaprtje KNJ za zrcaljenje Naj bo ponovno L nek KNJ s slovnico G, Slovnico za jezik LR tvorimo tako, da “obrnemo” desne strani (telesa) vseh produkcij slovnice G. Primer: Naj ima slovnica G produkciji: S -> 0 S 1 | 01. “zrcalni” jezik predstavimo z L(GR), ki ima produkciji: S -> 1 S 0 | 10. 21

Zaprtje KNJ za homomorfizem Naj bo ponovno L nek KNJ s slovnico G, Naj bo h homomorfizem na končnih simbolih slovnice G. Slovnico za h(L) tvorimo tako, da zamenjamo vsak končni simbol a s h(a) v vseh produkcijah slovnice G. 22

Primer: zaprtje za homomorfizem G ima produkciji: S -> 0 S 1 | 01. h je definirana tako, da: h(0) = ab, h(1) = ε. h(L(G)) ima slovnico s produkcijama: S -> ab. S | ab. 23

Zaprtje KNJ za inverzni homomorfizem 24 Za dokazovanje zaprtja za inverzni homomorfizem bomo, raje kot slovnico, uporabili SA. Naj bo L = L(P) za nek SA P. Tvorimo SA P’, ki bo sprejemal h-1(L). P’ bo simuliral P, imel bo 2 -komponentna stanja, kjer bo druga komponenta služila kot pomnilnik, kamor bomo shranjevali rezultate aplikacije funkcije h na posamezen vhodni simbol.

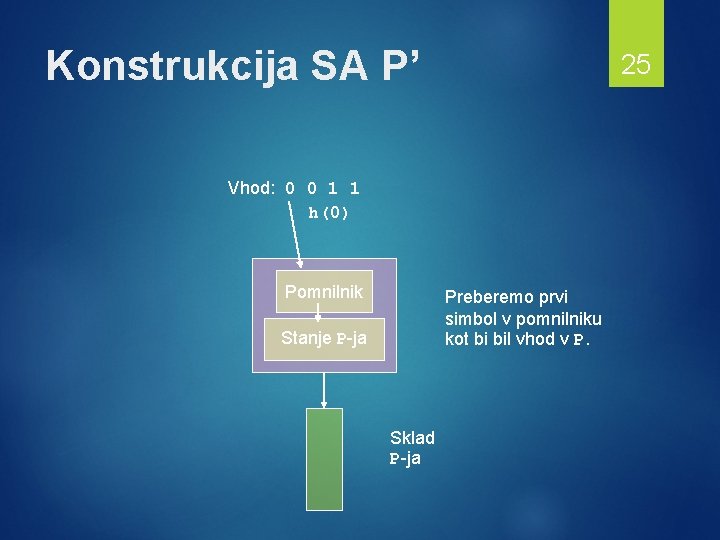
Konstrukcija SA P’ 25 Vhod: 0 0 1 1 h(0) Pomnilnik Preberemo prvi simbol v pomnilniku kot bi bil vhod v P. Stanje P-ja Sklad P-ja

Formalna konstrukcija P’ Stanja P’ so pari [q, w], kjer je: 1. q stanje P-ja. 2. w je pripona h(a) za nek simbol a. Torej: možnih vrednosti za w je le končno mnogo. 1. Simboli sklada SA P’ so enaki tistim od P. Začetno stanje P’ je [q 0, ε]. 26

Konstrukcija P’ – (2) Vhodni simboli SA P’ so simboli, na katerih lahko uporabimo homomorfizem h. 27 Končna stanja SA P’ so stanja [q, ε], tako da je q končno stanje SA P.

Prehodi v P’ 1. 28 δ’([q, ε], a, X) = {([q, h(a)], X)} za katerikoli vhodni simbol a skladovnega avtomata P’ in katerikoli simbol sklada X. 2. Ko se pomnilnik izprazni, ga P’ lahko ponovno “naloži”. δ’([q, bw], ε, X) vsebuje ([p, w], ), če δ(q, b, X) vsebuje (p, ), kjer je b bodisi vhodni simbol SA P ali pa ε. 1. Simulacija P-ja iz pomnilnika.

Dokazovanje pravilnosti P’ Pokazati je potrebno, da je L(P’) = h-1(L(P)). Ključni argument: 29 P’ naredi prehod ([q 0, ε], w, Z 0) ⊦* ([q, x], ε, ) natanko takrat, ko P naredi prehod (q 0, y, Z 0) ⊦* (q, ε, ), h(w) = yx ter je x pripona zadnjega simbola v w. Dokaz (v obe smeri) je indukcija po številu prehodov.

30 So KNJ zaprti za presek? Ne. Za razliko od regularnih jezikov, razred KNJ ni zaprt za . Vemo, da L 1 = {0 n 1 n 2 n | n > 1} ni KNJ (dokaz z lemo o napihovanju za KNJ). Ampak, L 2 = {0 n 1 n 2 i | n > 1, i > 1} je KNJ. KNS: S -> AB, A -> 0 A 1 | 01, B -> 2 B | 2. Prav tako, L 3 = {0 i 1 n 2 n | n > 1, i > 1} je KNJ (KNS? ) Ampak: L 1 = L 2 L 3.

Zaprtje za razliko 31 Pokažemo lahko nekaj splošnejšega: Vsak razred jezikov, ki je zaprt za razliko, je zaprt tudi za presek; In obratno: če nek razred jezikov ni zaprt za presek, ni zaprt niti za razliko; Dokaz: L M = L – (L – M). Torej: če bi bili KNJ zaprti za razliko, bi bili zaprti tudi za presek; ampak niso.

Presek z regularnim jezikom Presek dveh KNJ ni nujno spet KNJ. Ampak: presek KNJ z regularnim jezikom je vedno KNJ. Dokaz vključuje poganjanje DKA vzporedno s SA, kar je enakovredno poganjanju nekega SA. SA sprejema na podlagi končnega stanja. 32

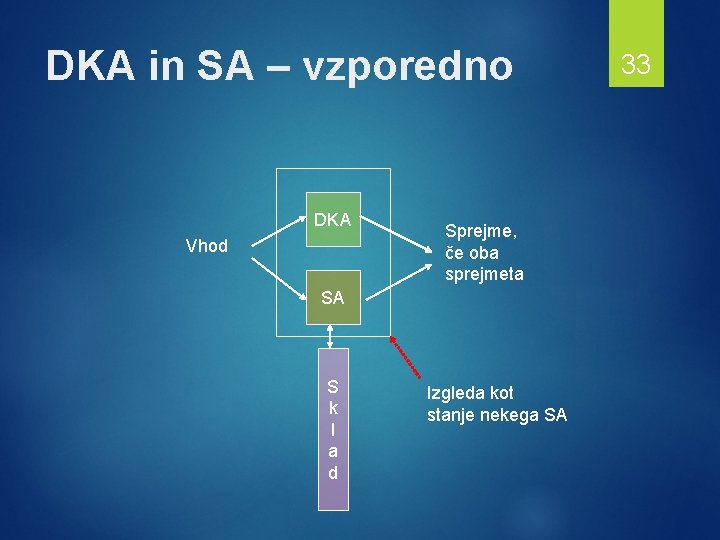
DKA in SA – vzporedno DKA Vhod Sprejme, če oba sprejmeta SA S k l a d Izgleda kot stanje nekega SA 33

Formalna konstrukcija Naj ima DKA A funkcijo prehoda δA. Naj ima SA P funkcijo prehoda δP. Stanja “kombiniranega” SA so oblike [q, p], kjer je q stanje DKA A, p pa stanje SA P. δ([q, p], a, X) vsebuje ([δA(q, a), r], ), če δP(p, a, X) vsebuje (r, ). Pozor: a je lahko , v tem primeru je δA(q, a) = q. 34

Formalna konstrukcija – (2) 35 Končna stanja “kombiniranega” SA so tista stanja [q, p], pri katerih je q končno stanje DKA A, p pa končno stanje SA P. Začetno stanje je par [q 0, p 0], ki vsebuje začetni stanji A in P. Preprosta indukcija: ([q 0, p 0], w, Z 0) ⊦* ([q, p], , ) natanko takrat, ko je δA(q 0, w) = q in za P velja: (p 0, w, Z 0) ⊦* (p, , ).