Seminarska naloga Analiza neodvisnih komponent ICA Fakulteta za

Seminarska naloga Analiza neodvisnih komponent (ICA) Fakulteta za elektrotehniko Avtor: Alan Keber Mentor: prof. Dr. Stanislav Kovačič

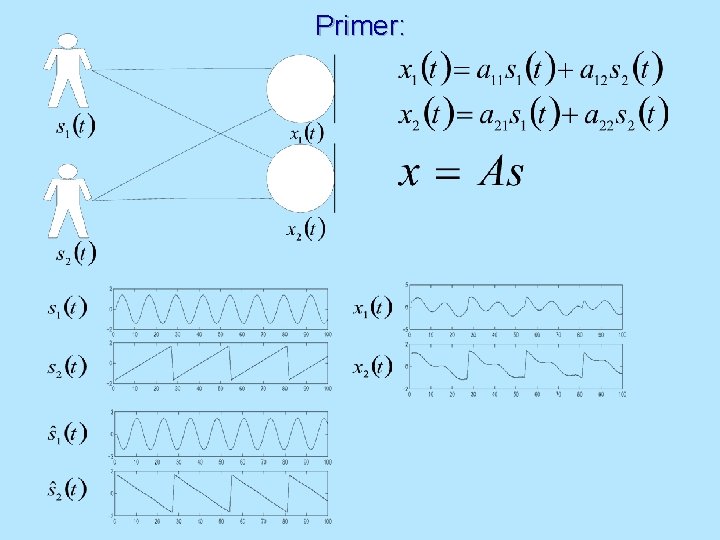
Primer:

Statistična neodvisnost Definicija za statistično neodvisnost: Naključne spremenljivke y so medsebojno neodvisne, če je funkcija gostote verjetnosti enaka produktu gostot verjetnosti za vsako spremenljivko posebej. Definicija nekoreliranosti: Če so naključne spremenljivke medsebojno statistično neodvisne, so tudi nekorelirane, obratno pa ne velja. Potreben, vendar ne zadosten pogoj za statitistično neodvisnost je nekoreliranost. Nekoreliranost je zadosten pogoj za neodvisnost le vprimeru Gaussove porazdelitve naključnih spremenljivk.

Primer: Imamo dve neodvisni spremenljivki s, ki so uniformno porazdeljene, so neodvisne in nekorelirane (spodnja slika levo). Če je matrika A ortogonalna in če monžimo matriko A z vektorjem naključnih spremenljivk s po spodnji enačbi, potem dobimo vektor naključnih spremenljivk x (spodnja slika desno), za katere velja: • naključne spremenljivke x so nekorelirane • x so statistično odvisne

Definicija linearnega ICA Iskanje statistično neodvisnih spremenljivk s iz meritev x sestoji iz določanja linearne treansformacije oz. matrike W tako , da velja enačba: Matriko W iščemo s pomočjo maksimizacije ali minimizacije kriteriske funkcije: Kriterijska funkcija je merilo za statistično neodvisnost. Velja tudi spodnja enačba: kjer je:

Določljivost ICA modela Enačba modela ICA: Model ICA je možno določiti, če velja : • statistično neodvisne spremenljivke s ne smejo biti porazdelejne po Gaussu, razen ene • število meritev x mora biti vsaj toliko veliko, kot je število neodvisnih spremenljivk s • matrika A mora biti polnega ranga Primer: Dve naključni spremenljivki s porazdeljeni po Gaussu. Ker je simetrična porazdelitev, bo ne glede na matriko A ostala (ortogonalna matrika), ostala enaka.

Kriterijske funkcije za ocenitev ICA modela Kurtosis: Je kriterij za merjenje, koliko so naključne spremenljivke s porazdeljena po Gaussu oz. koliko niso. Če je naključna spremenljivka porazdeljena po Gaussu, potem je vrednost kurt(s)=0 Diferenčna entropija: Definicija entopije: Največja vrednost entropije je, kadar so naključne spremenljivke porazdeljene po Gaussu, vse z enako varianco. Zato lahko zapišemo kriterijsko funkcijo (spodnja enačba), ki bo vedno večja ali enaka 0. 0 bo le v primeru, ko bodo naključne spremenljivke porazdeljene po Gaussu.

Aproksimacija diferenčne entropije: Ker je računanje kriterijske funkcije po enačbi za diferenčno entropijo računsko prezahtevna naloga, se poslužujemo pribljižka po spodnji enačbi: je Gaussova spremenljivka, za katero velja: Primeri za funkcijo G: Z aproksimacijo diferenčne entropije dosežemo kompromis med lastnostmi Kurtosisa in lastnostmi diferenčne entropije.

Predobdelava podatkov Pred samo izvedbo ICA algoritma, je koristno, če se izvede predobdelava vektorja naključnih spremenljivk x. Centriranje: Vektorju naključnih spremenljivk odštejemo njegovo povprečno vrednost. Beljenje: Prva predpostavka je, da je vektor x je centriran po zgornjem postopku. Če vektor x še dekoreliramo, potem smo že bližje statistični neodvisnosti (x je nekoreliran). Vektor x je nekoreliran, če je cov(x)=I. Postopku, ki doseže, da je cov(v)=I, pravimo beljenje. Postopek beljenja poteka s pomočjo PCA metode. • E je matrika lastnih vektorjev po PCA metodi • D matika lastnih vrednosti po diagonali

Če je cov(s)=cov(v)=I => B je ortogonalen. Primer beljenja: Primer prikazuje vektor x, ki je sestavljen iz linearne transformacije dveh neodvisnih naključnih spremenljivk z uniformno porazdelitvijo (slika desno). Slika desno prikazuje pobeljen vektor naključnih spremenljivk.

Preizkus FP-ICA algoritma na slikah Izbral sem FP-ICA algoritem, ki temelji na maksimizacije funkcije Kurtosisa. Pogoj za delovanje tega algoritma je da je vektor x predhodno centriran in pobeljen. Dobra lastnost tega algoritma je, da hitro konvergira proti rešitvi. 1. preizkus: • dve 8 bitni bmp sivi sliki dimenzij 112 x 92 • vsako sliko predstavimo kot vektor p dimenzije 112 x 92 • naredil x=Hp, kjer je H permutacijska matrika polnega ranga • preko FP-ICA ocenil s • narisal s 2. preizkus: • 24 bitna RGB bmp slika dimenzij 640 x 480 • sliko ločil na R, G, B, kjer vsaka komponenta predstavlja svoj vektor dimenzije 640 x 480 • preko FP-ICA ocenil s • Združil zopet v 24 bitno RGB sliko in jo narisal

1. preizkus:

2. preizkus: Originalna slika Ocenjena slika

Originalna slika Ocenjena slika Uporaba ICA: • Magnetocefalografija • ekonomija (iskanje skritih faktorjev v finančnih podatkih) • čiščenje šuma iz slike • telekomunikacije

Literatura § Hyvärinen, A. , Oja, E. (1999) Independent Component Analysis: Algorithms and Applications. Neural Networks. § Hurri, J. (1997) Independent component analysis of image data. Master thesis, Dept. of Computer Science and Engineering, Helsinki University of Technology. § Hyvärinen, A. , Oja, E. (1997) A Fast Fixed-Point Algorithm for Independent Component Analysis. Neural Computation, 9: 1483 -1492. § Hyvärinen, A. (1999) Fast and Robust Fixed-Point Algorithms for Independent Component Analysis. IEEE Trans. On Neural Networks. § Hyvärinen, A. Survey on Independent Component Analysis. URL naslov: http: //www. cis. hut. fi/~aapo/ (20. 4. 2003)

KONEC Hvala za potrpežljivost.