1 Arrays and invariants Arrays An ordered collection

1. Arrays and invariants

Arrays • An ordered collection of elements of the same type – Primitive types (int, double, char, boolean, . . – References to objects (Strings, …) • Size is determined at creation and cannot be modified 2

Arrays of primitive types int[] x; // equivalent to int x[] x = new int[3]; x[0] = 10; x[1] = 20; x[2] = 30; X 10 20 30 Note: x. length is a final int variable with the size 3

Arrays of Objects Referencias X Circle[] x; x = new Circle[3]; x[0] = new Circle(); x[1] = new Circle(); x[2] = new Circle(); 4

Arrays of Arrays • Java allows creating arrays of arrays using the following syntax int[][] m = new int[4][]; for (int i = 0; i < m. length; i++) { ma[i] = new int[i+1]; for (int j = 0; j < m[i]. length; j++) { m[i][j] = i + j; } } 5

Arreglos de Strings • Paso de parámetros Static public void main(String[] args) { for (int i = 0; i < args. length; i++) { System. out. println(″Argumento ″+(i+1)+ ″ = ″+args[i]); } } 6

Initializing Arrays • Syntax for initializing arrays: boolean[] respuestas = {true, false, true}; String[] nombres = {"Ana María", "Carlos"}; String[][] geography = { { “Asia", “Japan“, “China”}, { “America“, “USA”, “Canada”, “Brazil”, ”Mexico” }, { “Europe", “Germany", “Poland", “Belgium" } }; 7

Example: Searching for the index of the biggest number: Invariant Strategy: pass trhough all elements a[0] to a[n-1] and register the index of the biggest seen so far Invariant: a[m] = max(a[0] … a[k-1]), 1 <= k < n a 0 a 1 . . . ak-1 ak m . . . an-1 k static int mindex(int[] a) { int m =0, k = 1; while(k <= a. length){ if (a[k] > a[m] ) m = k; k++ return m; }

The invariant of an iteration Invariant: A set of conditions describing the strategy Frequently used to explain what an iteration does Also formally prove that the iteration achieves what it should Should be true at before beginning the iteration (while, for), during the iteration and after ending it • The invariant and the negation of the iteration condition should describe the achievement of the task • •

Initial and final conditions a) At the beginning we have seen no number, so we asume the first one is the biggest by doing m = 0] and k = 1; and the invariant holds a 0 a 1 . . . ai . . . an-1 k b) In order to achieve the goal k must be equal to n so the while should stop when k == n, or continue while k != n, or k < n a 0 a 1 . . . ai . . . an-1 k

Inside the while c) In order to make k closer to n we must increase its value. Howerver, this might break the invariant. k++; a 0 a 1 . . . ai ai+1 . . . an-1 k Unless we make sure that when we increase the value of k by 1 the value of m still points to the biggest element if (a[k] < m) m = a[k];

Another example: ordering by selection Based on selecting the biggest among the (remaining) elements and put it at the right side of the array before the one which was “selected” in the previous iteration. The invariant looks like this: • a[i] < a[i+1] for i = k to n-1 • a[j] < a [i] with j = 0 to k-1, not sorted and all smaller than a[k]

Initial and final conditions a) Initial: make k = n, which implies: • a[i] < a[i+1] for i = n to n-1 sorted (no element) • a[j] < a [n] for j = 0 to n-1, not sorted ¿More intuitive? : before entering the loop put the biggest in n-1 and make k= n-1 b) final: k = 1 (or while k >= 2) • a[i] < a[i+1] for i = 1 to n-1 • a[j] < a [1] for j = 0 to 0, not sorted but smaller tan a[1]

Program // sort a[0], . . . , a[n-1] by selection k = n; // initially all n elemnts are not sorted while( k>1 ) { --k; //bring k closer to the goal, invariant may not hold bring the max of a[0], . . . , a[k] to a[k]; //invariant is fixed } Where bring the max of a[0], . . . , a[k] to a[k]; => i = 0; // a[i] is the biggest so far for( j=1; j<=k; ++j ) if( a[j]>a[i] ) i = j; // now we exchange a[i] with a[k] t = a[i]; a[i] = a[k]; a[k] = t;

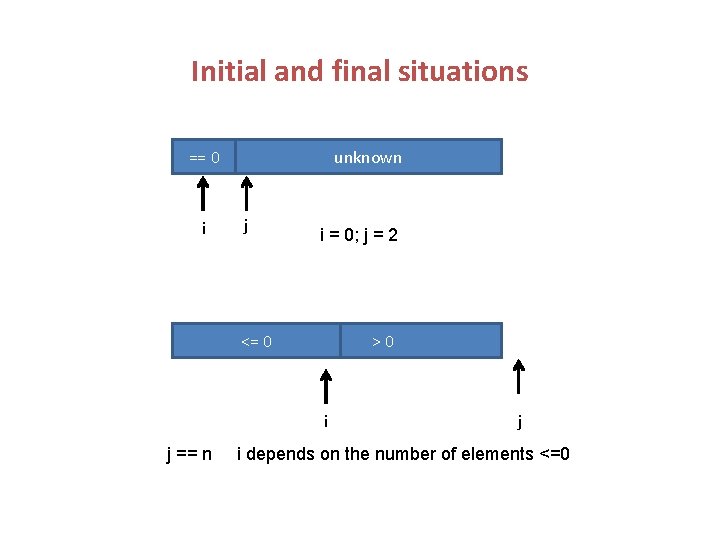
Another example We have an array a[0]. . . a[n-1] with integers (positive and negatives) and we want to put all the numbers <=0 at the left (not sorted) and the numbers > 0 a the right. The frst one is =0 Lets use the following invariant: all elements until a[i] (included) are <=0, all elements from a[i+1] to a[j-1] are >0, from a[j] on are unknown <= 0 > 0 i unknown j

Initial and final situations == 0 i unknown j i = 0; j = 2 <= 0 > 0 i j == n j i depends on the number of elements <=0

Bringing j to n If a[j] <= 0 we increment only j, else we Exchange a[i] with a[j] and we increment j and i <= 0 > 0 i unknown j static int divide(int[] a) { int i=0, j = 1; while(k < a. length){ if (a[j] <=0 ) { int aux = a[i+1]; a[i+1] = a[j]; a[j]= aux; i++; } j++ } return m; }

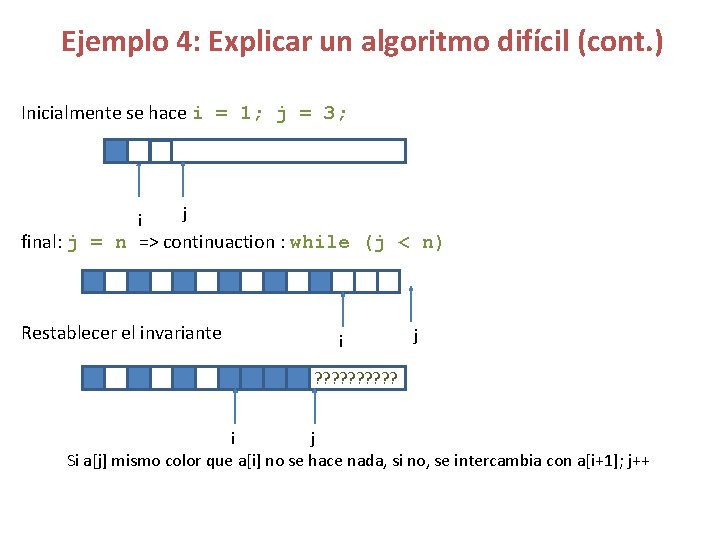
Even harder to undertand without invariant We have an array with n elements (a[0] … a[n-1]) blue and White unsorted. Leave the elements interleved (one blue, one White …). If there are more elements from one color tan another leave the remainding of the same color at the end. Assume that at the beginning we have one blue followed by two White elements Example, if inicialy we have At the end they should be in the following positions invariante ? ? ? i j

Ejemplo 4: Explicar un algoritmo difícil (cont. ) Inicialmente se hace i = 1; j = 3; i j final: j = n => continuaction : while (j < n) Restablecer el invariante i j ? ? ? ? ? i j Si a[j] mismo color que a[i] no se hace nada, si no, se intercambia con a[i+1]; j++

Ejemplo 4: Xn Cuando n es entero se puede programar una función más eficiente que la que usa java, basada en el cálculo de una serie. public static double power(double x, int n) { // Algoritmo simple int y = 1; for( int j=n; j>0; --j ) y = y*x; return y; } algoritmo O(n), y su invariante se puede escribir como y * xj == xn

Aprovechando el invariante para la eficiencia Es posible encontrar un algoritmo sustancialmente más eficiente de la siguiente manera. public static double power(double x, int n) { int j = n; long z = x; int contador = 0; while (j>1) { if (j%2 == 0){ z = z*z; j = j/2; } else { z = x*z; j = j-1; } } System. out. println(“Resultado = "+z); } con invariante z* xj == xn

Algoritmo algo más eficiente aún Sacando x del invariante public static double power(double x, int n) { int y = 1, z = x; for( int j=n; j>0; --j ) { while( j%2 == 0) { z = z*z; j = j/2; } y = y*z; } Con invariante y * zj = xn