Computer Graphics Filling Filling Polygons So we can

Computer Graphics Filling

Filling Polygons • So we can figure out how to draw lines and circles • How do we go about drawing polygons? • We use an incremental algorithm known as the scan-line algorithm

Polygon • Ordered set of vertices (points) – Usually counter-clockwise • • • Two consecutive vertices define an edge Left side of edge is inside Right side is outside Last vertex implicitly connected to first In 3 D vertices are co-planar 3

Filling Polygons • Three types of polygons 1. Simple convex 2. simple concave 3. non-simple (self-intersection) Convex polygons have the property that intersecting lines crossing it either one (crossing a corner), two (crossing an edge, going through the polygon and going out the other edge), or an infinite number of times (if the intersecting line lies on an edge).

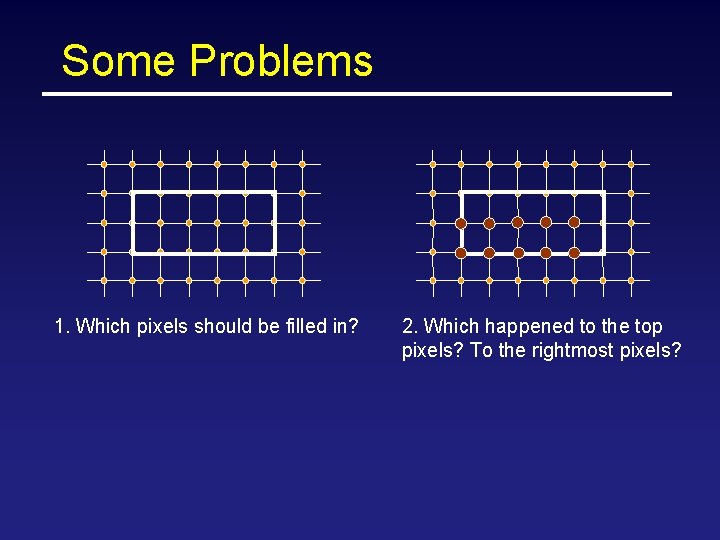
Some Problems 1. Which pixels should be filled in? 2. Which happened to the top pixels? To the rightmost pixels?

Scan-Line Polygon Example Polygon Vertices Maxima / Minima Edge Pixels Scan Line Fill

Scan Line Algorithms Create a list of vertex events (bucket sorted by y)

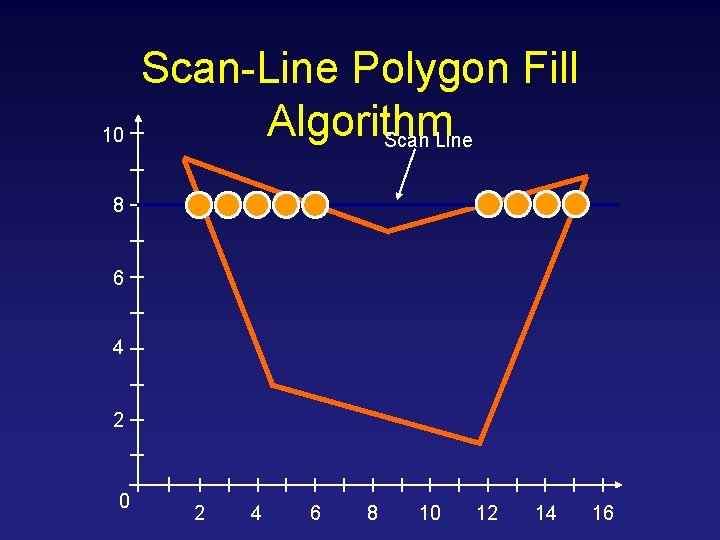
10 Scan-Line Polygon Fill Algorithm Scan Line 8 6 4 2 0 2 4 6 8 10 12 14 16

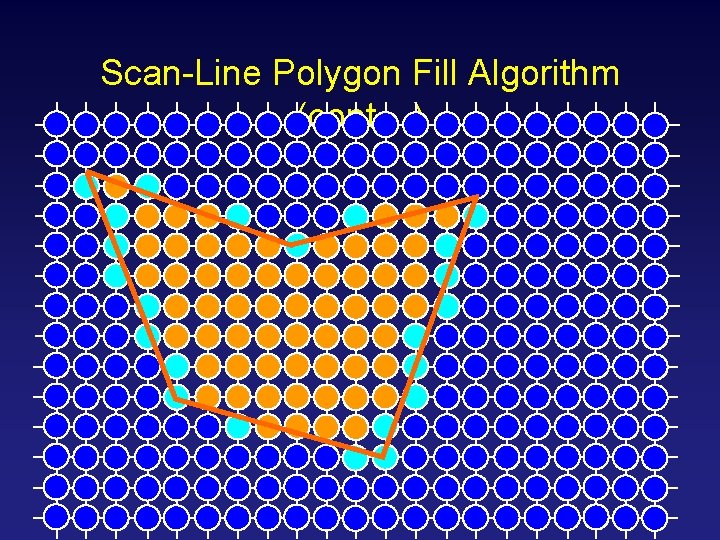
Scan-Line Polygon Fill Algorithm • The basic scan-line algorithm is as follows: – Find the intersections of the scan line with all edges of the polygon – Sort the intersections by increasing x coordinate – Fill in all pixels between pairs of intersections that lie interior to the polygon

Scanline Algorithms • given vertices, fill in the pixels triangles • split into two regions • fill in between edges arbitrary polygons (non-simple, non-convex) • build edge table • for each scanline • obtain list of intersections, i. e. , AEL • use parity test to determine in/out and fill in the pixels 10

Scan-Line Polygon Fill Algorithm (cont…)

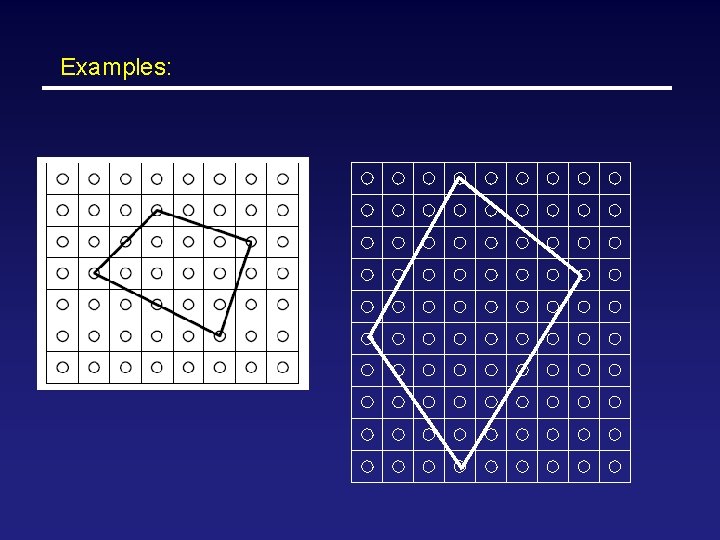
Examples:

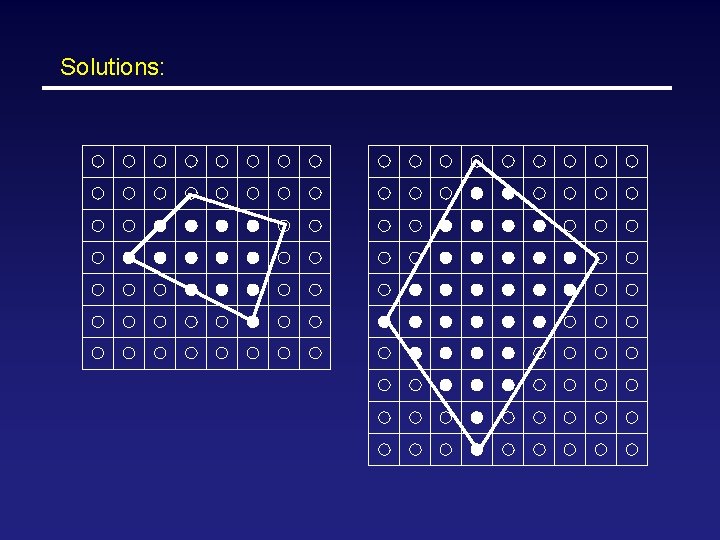
Solutions:

Scan Line Algorithms Create a list of the edges intersecting the first scanline Sort this list by the edge’s x value on the first scanline Call this the active edge list

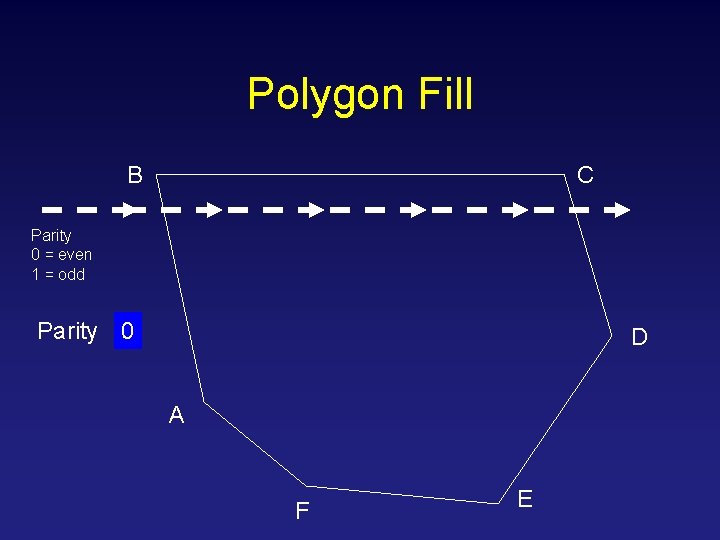
Polygon Fill B C Parity 0 = even 1 = odd Parity 0 1 D A F E

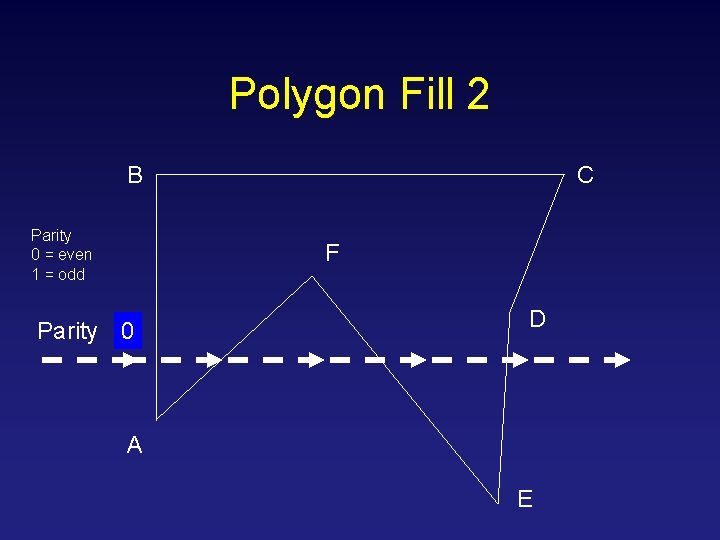
Polygon Fill 2 B Parity 0 = even 1 = odd C F Parity 0 1 D A E

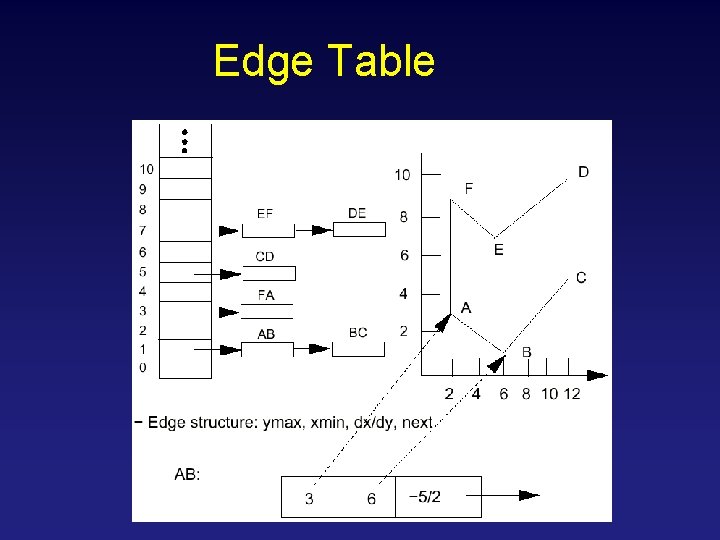
Edge Tables • edge table (ET) – store edges sorted by y in linked list • at ymin, store ymax, xmin, slope • active edge table (AET) – active: currently used for computation – store active edges sorted by x • update each scanline, store ET values + current_x – for each scanline (from bottom to top) • do EAT bookkeeping • traverse EAT (from leftmost x to rightmost x) – draw pixels if parity odd

Scanline Rasterization Special Handling • Intersection is an edge end point, say: (p 0, p 1, p 2) ? ? • (p 0, p 1, p 2), so we can still fill pairwise • In fact, if we compute the intersection of the scanline with edge e 1 and e 2 separately, we will get the intersection point p 1 twice. Keep both of the p 1.

Scanline Rasterization Special Handling • But what about this case: still (p 0, p 1, p 2)

Edge Table

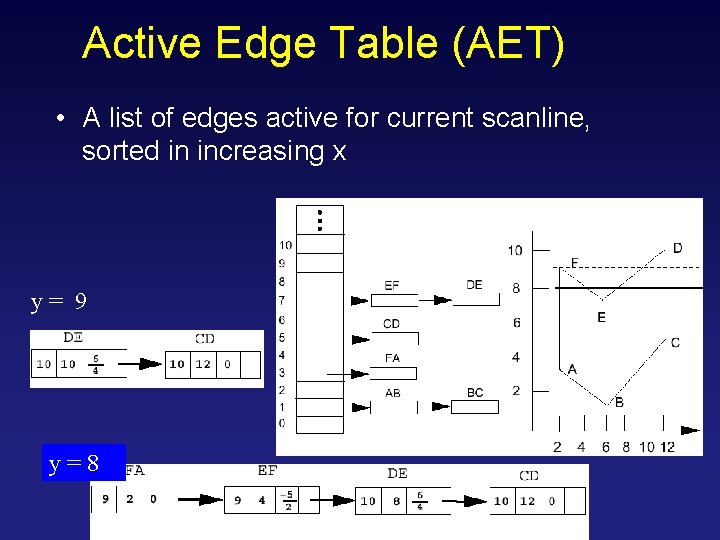
Active Edge Table (AET) • A list of edges active for current scanline, sorted in increasing x y= 9 y=8

Edge Table Bookkeeping • setup: sorting in y – bucket sort, one bucket per pixel – add: simple check of ET[current_y] – delete edges if edge. ymax > current_y • main loop: sorting in x – for polygons that do not self-intersect, order of edges does not change between two scanlines – so insertion sort while adding new edges suffices

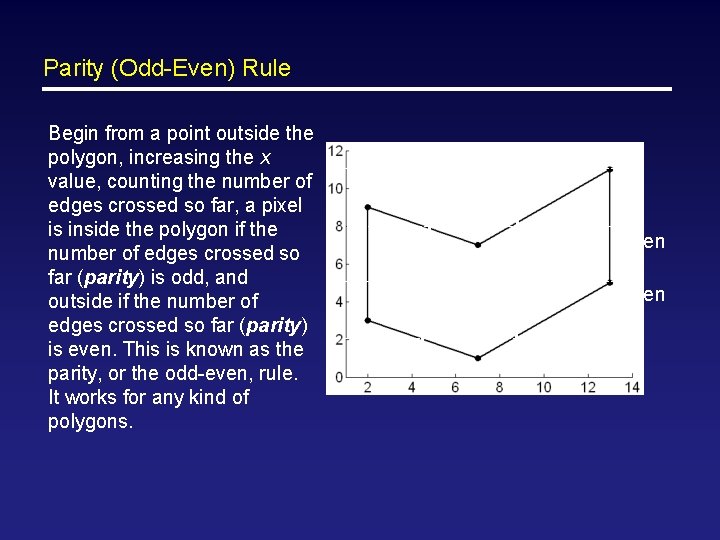
Parity (Odd-Even) Rule Begin from a point outside the polygon, increasing the x value, counting the number of edges crossed so far, a pixel is inside the polygon if the number of edges crossed so far (parity) is odd, and outside if the number of edges crossed so far (parity) is even. This is known as the parity, or the odd-even, rule. It works for any kind of polygons. Parity starting from even odd odd even

Polygon Scan-conversion Algorithm Construct the Edge Table (ET); Active Edge Table (AET) = null; for y = Ymin to Ymax Merge-sort ET[y] into AET by x value Fill between pairs of x in AET for each edge in AET if edge. ymax = y remove edge from AET else edge. x = edge. x + dx/dy sort AET by x value end scan_fill

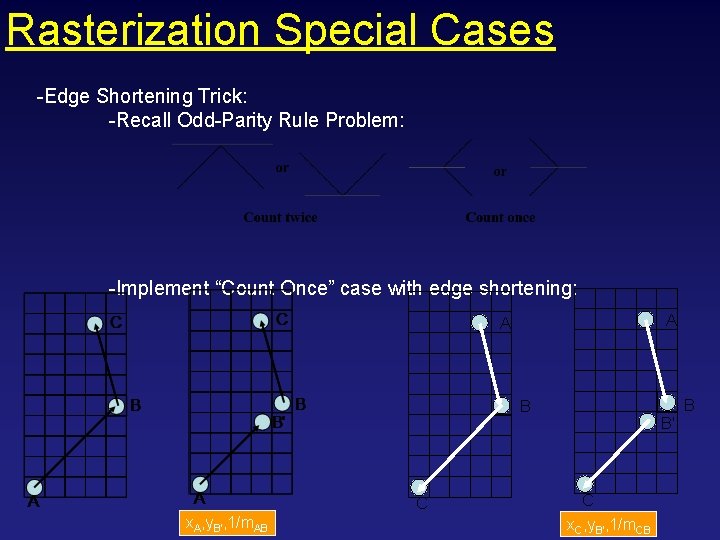
Rasterization Special Cases -Edge Shortening Trick: -Recall Odd-Parity Rule Problem: -Implement “Count Once” case with edge shortening: A A B C x. A, y. B’, 1/m. AB B' C x. C, y. B’, 1/m. CB B

Scan Line Algorithms For each scanline: 1. Maintain active edge list (using vertex events) 2. replace insert delete Increment edge’s x-intercepts, sort by x-intercepts 3. Output spans between left and right edges

Penetrating Polygons False edges and new polygons! Compare z value & intersection when AET is calculated

Flood Fill • 4 -fill – Neighbor pixels are only up, down, left, or right from the current pixel • 8 -fill – Neighbor pixels are up, down, left, right, or diagonal

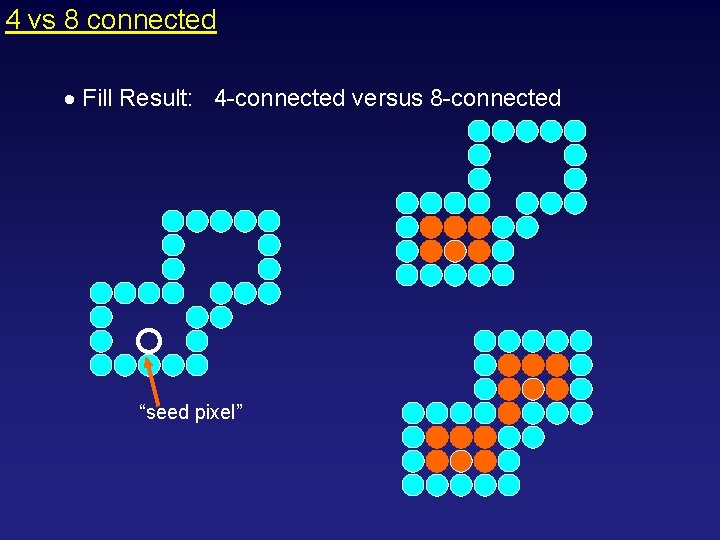
4 vs 8 connected Define: 4 -connected versus 8 -connected, its about the neighbors

4 vs 8 connected Fill Result: 4 -connected versus 8 -connected “seed pixel”

Flood Fill • Algorithm: 1. Draw all edges into some buffer 2. Choose some “seed” position inside the area to be filled 3. As long as you can 1. “Flood out” from seed or colored pixels » 4 -Fill, 8 -Fill

Flood Fill Algorithm Seed Position Edge “Color” void boundary. Fill 4(int x, int y, int fill, int boundary) { Fill “Color” int curr; curr = get. Pixel(x, y); if ((current != boundary) && (current != fill)) { set. Color(fill); set. Pixel(x, y); boundary. Fill 4(x+1, y, fill, boundary); boundary. Fill 4(x-1, y, fill, boundary); boundary. Fill 4(x, y+1, fill, boundary); boundary. Fill 4(x, y-1, fill, boundary); } }

Example Let’s apply the rules to scan line 8 below. We fill in the pixels from point a, pixel (2, 8), to the first pixel to the left of point b, pixel (4, 8), and from the first pixel to the right of point c, pixel (9, 8), to one pixel to the left of point d, pixel (12, 8). For scan line 3, vertex A counts once because it is the ymin vertex of edge FA, but the ymax vertex of edge AB; this causes odd parity, so we draw the span from there to one pixel to the left of the intersection with edge CB. D F b a odd even c d even odd E C A B

Four Elaborations (cont. ) G G F H I E E C J A B D

Halftoning For 1 -bit (B&W) displays, fill patterns with different fill densities can be used to vary the range of intensities of a polygon. The result is a tradeoff of resolution (addressability) for a greater range of intensities and is called halftoning. The pattern in this case should be designed to avoid being noticed. These fill patterns are chosen to minimize banding.