1 2 Differential Calculus Christopher Crawford PHY 311

§ 1. 2 Differential Calculus Christopher Crawford PHY 311 2014 -01 -22

Key Points up to Now • Linear spaces – Linear combinations / projections -> basis / components – Dot product reduces; Cross product builds up dimension (area, vol. ) – Orthogonal projections (Dot = parallel, Cross = perpendicular) • Linear operators – Most general transformation is a rotation * stretch – Rotations (orthogonal) appear in coordinate transformations – Stretches (symmetric) occur in orthogonal directions (eigenspaces) 2

Where are we heading? • Differential spaces – – – Everything follows from the differential (d) and chain rule (partials) Differential (line, area, vol. ) elements are ordered by dimension The derivative increases to one higher dimension There is only ONE 1 st derivative: d or in different dimensions There is only ONE 2 nd derivative: the Laplacian • Affine space/curvilinear coordinates – – Operations on points and vectors: affine combination Position vector: connection between point and vector Coordinates: used to parameterize a volume / surface / curve Differential d is more natural than for curvilinear coordinates • 2 classes: Integration / Stokes’ theorems / Poincaré lemma • 2 classes: Delta fn / Green’s fn / Helmholtz theorem / fn spaces – These 4 types of fundamental theorems map directly onto electrodynamic principles (and all classical fields) 3

Outline • Differential operator – `d’ Calculus of a single variable • • Partial differentials – chain rule Gradient, vector differential (del operator) Differential line, area, volume elements (dl, da, d¿) Relation between d, , dr • Curl and Divergence – differential in higher dimensions Geometric interpretation (boundary) • Laplacian – unique 2 nd derivative: curvature Projection into longitudinal / transverse components • Unified approach to all derivatives using differential `d’ 4

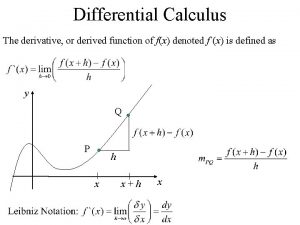
Differential operator • Definition – Infinitesimal – Relation between differentials – Becoming finite: ratio / infinite sum – Chain rule 5

Partial differentials • Partial differential • Chain rule • Partial derivative • List of differentials 6

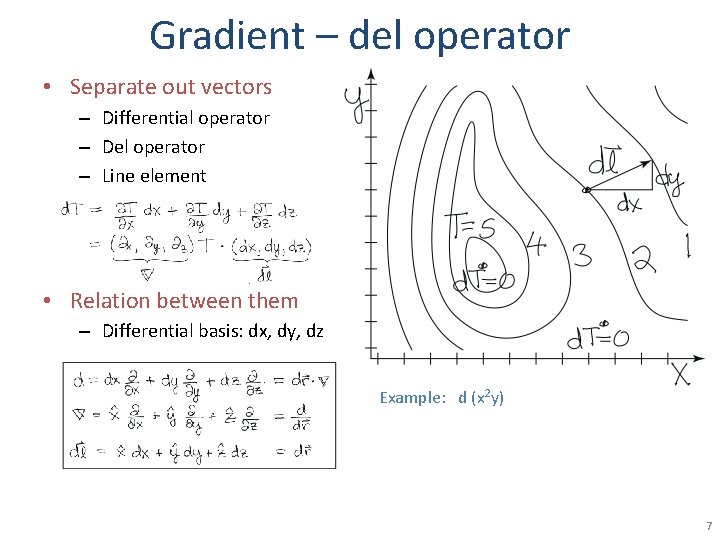
Gradient – del operator • Separate out vectors – Differential operator – Del operator – Line element • Relation between them – Differential basis: dx, dy, dz Example: d (x 2 y) 7

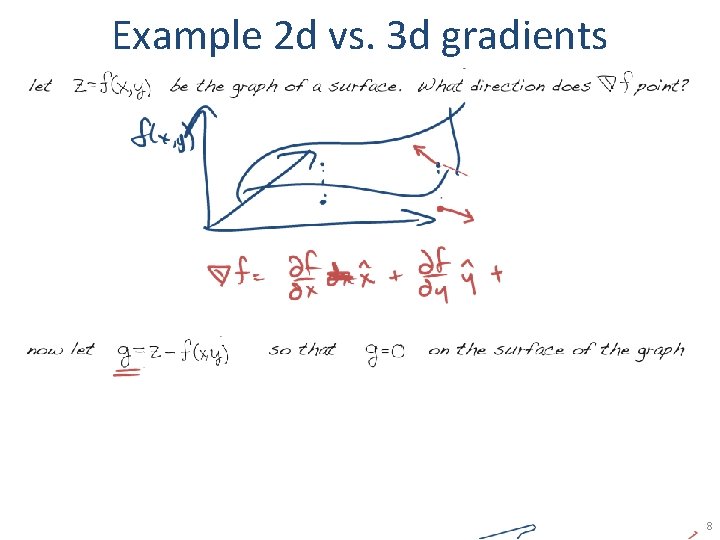
Example 2 d vs. 3 d gradients 8

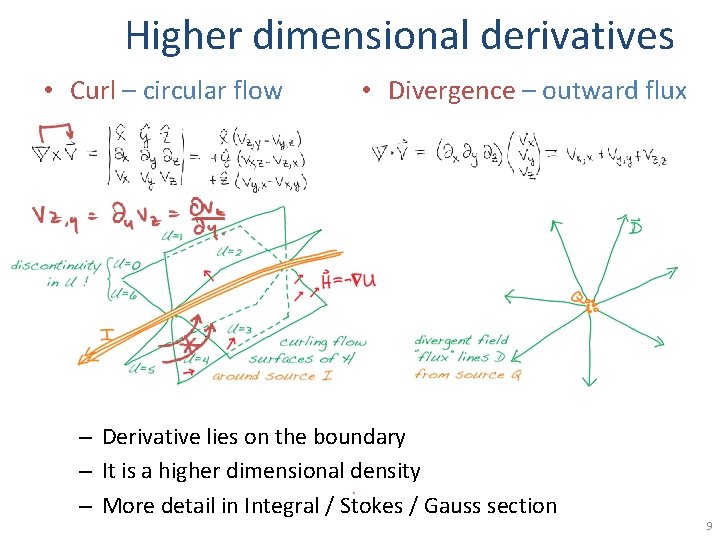
Higher dimensional derivatives • Curl – circular flow • Divergence – outward flux – Derivative lies on the boundary – It is a higher dimensional density – More detail in Integral / Stokes / Gauss section 9

Product Rules • Combine vector and derivative rules • How many distinct products? (combinations of dot, cross) 10

nd 2 derivative: the Laplacian • Net curvature of a scalar function; Net ? ? ? of a vector function? • How many 2 nd derivatives? (combinations of dot, cross) 11

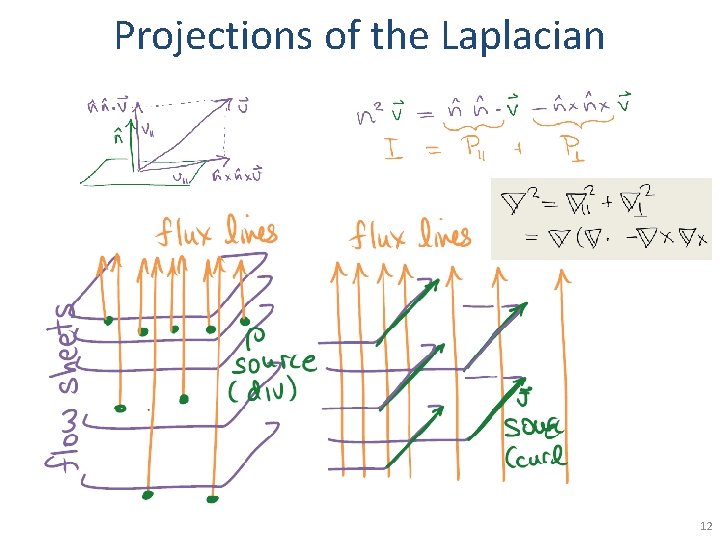
Projections of the Laplacian 12

Unification of vector derivatives • Three rules: a) d 2=0, b) dx 2 =0, c) dx dy = - dy dx • Differential (line, area, volume) elements as transformations 13